1.4.2 箱ひげ図 〜統計検定2級対応・統計学入門まとめ〜

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.4.2$節「箱ひげ図」の内容を元に$5$数要約の可視化にあたって用いられる箱ひげ図の概要や描き方に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

田中豊, 中西寛子, 姫野哲人, 酒折文武, 山本義郎

2,420円(09/18 07:43時点)

Amazon

箱ひげ図の概要

概要

$5$数要約を用いることで四分位範囲や中央値を元に観測値を把握することができますが、単に計算結果だけではなく図を用いて可視化を行うことでより直感的な把握が可能になります。$5$数要約の可視化にあたってよく用いられるのが箱ひげ図(box whisker plot)です。

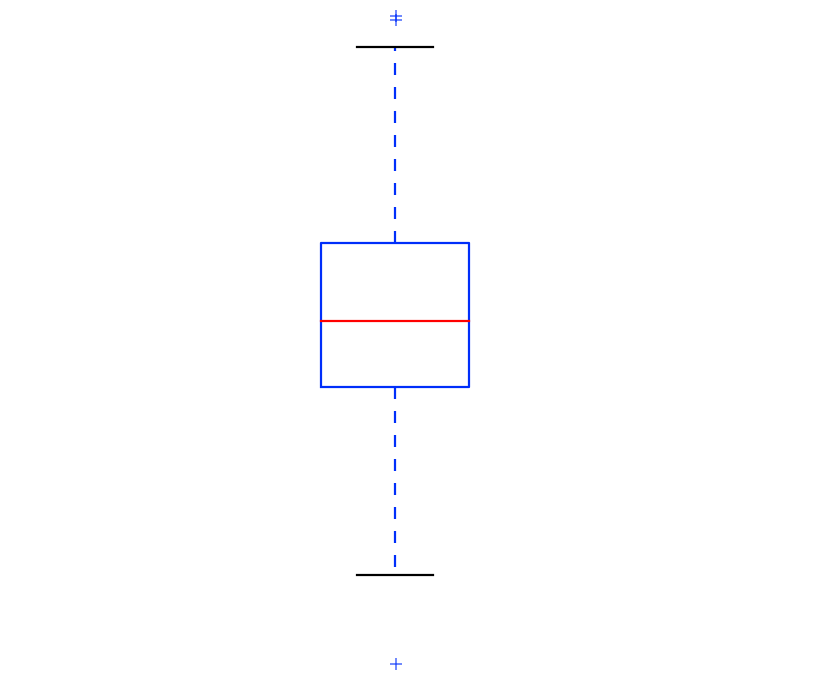
箱ひげ図は上図のような図であり、第$1$四分位数と第$3$四分位数を元に箱を作成し、中央値を箱の中に書き入れます。ひげの描き方はいくつかあるので詳しくは次節や「$1.4.3.$ 外れ値」などで確認します。

必要な数学

中央値、四分位数を主に取り扱うので、$2$級範囲では数学知識は特に必要ありません。

箱ひげ図

箱ひげ図の解釈

上図のような箱ひげ図の解釈にあたっては、箱によって第$1$四分位数$Q1$と第$3$四分位数$Q2$が表され、箱の中に中央値が記入されることをまず抑えると良いです。ひげの描き方は最大値・最小値を元に作成する場合と、四分位範囲$IQR$を元に作成する場合などがあります。上図では「$1.4.3.$ 外れ値」の内容も考慮し、$Q3 + 1.5 IQR$と$Q1 – 1.5 IQR$を元にひげを作成しました。+のマーカーは例外のような観測値であると解釈しておけば良いです。

Pythonを用いた箱ひげ図の作成

下記を実行することでPythonで箱ひげ図を作成することができます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x1 = stats.norm.rvs(loc=0,scale=1,size=100)
x2 = stats.norm.rvs(loc=0,scale=1.5,size=100)
x3 = stats.norm.rvs(loc=1,scale=1,size=100)

plt.boxplot([x1, x2, x3])
plt.show()

・実行結果

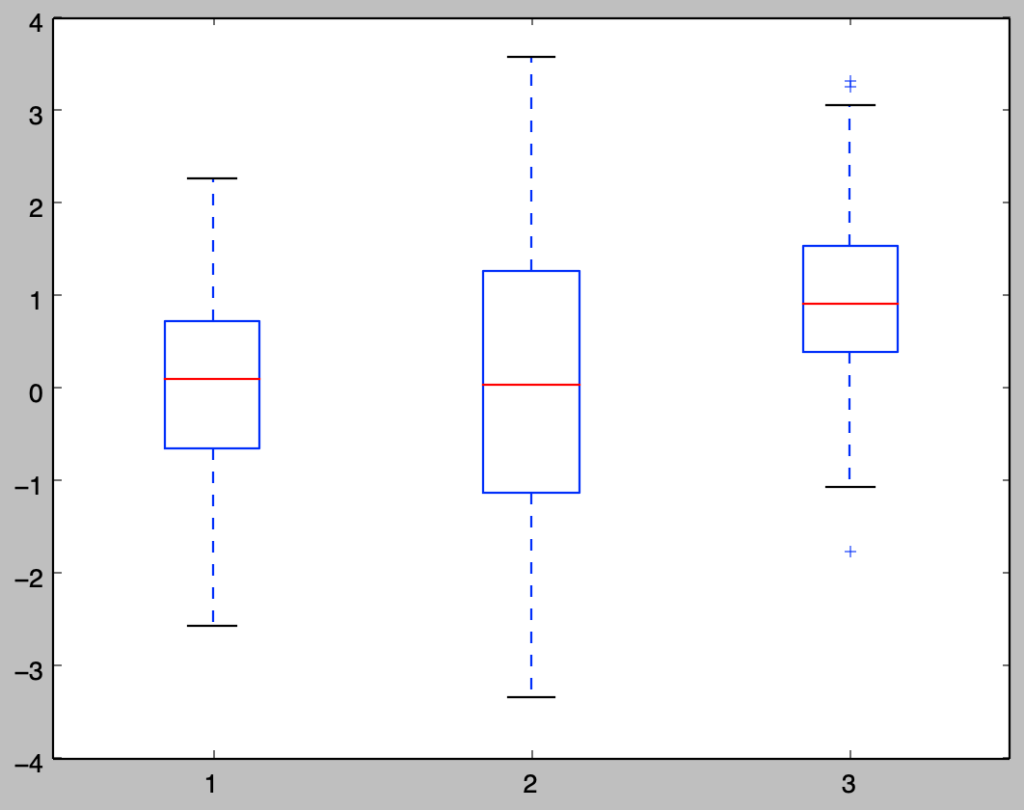
上記はx1が$\mathcal{N}(0,1^2)$に基づくサンプル、x2が$\mathcal{N}(0,1.5^2)$に基づくサンプル、x3が$\mathcal{N}(1,1^2)$に基づくサンプルにそれぞれ対応しますが、概ね妥当な結果が得られたことが確認できると思います。