当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.6.2$節「相関係数」の内容を元に$2$変数の相関を確認するにあたって用いられることの多い相関係数に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
Contents
相関係数の概要
概要
「$1.6.1$ 散布図と相関」では$2$変数の相関を散布図を元に確認しましたが、散布図のように定性的ではなく定量的に相関を計算するのが当記事で取り扱う相関係数です。相関係数は$2$変数それぞれの分散と共分散を用いて定義する指標ですが、詳しくは以下で取り扱います。
必要な数学
相関係数の式の定義にあたっては$\displaystyle \sum$が用いられるので抑えておくと良いです。
また、相関係数はベクトルの内積を元に表すと理解しやすいので、ベクトルと内積を抑えておくと良いと思います。
相関係数
共分散の定義式
$x_1, \cdots , x_n$と$y_1, \cdots , y_n$の平均$\bar{x}, \bar{y}$と標準偏差$s_x, s_y$をそれぞれ下記のように定義します。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{n} \sum_{i=1}^{n} x_i \\
s_x &= \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})^2 }
\end{align}
$$
$$
\large
\begin{align}
\bar{y} &= \frac{1}{n} \sum_{i=1}^{n} y_i \\
s_y &= \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i-\bar{y})^2 }
\end{align}
$$
このとき$x, y$の共分散$s_{xy}$は下記のように定義されます。
$$
\large
\begin{align}
s_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})
\end{align}
$$
共分散の解釈
共分散の解釈にあたっては下記のように$(\bar{x},\bar{y})$に着目して考えると良いです。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x = stats.uniform.rvs(0., 10., size=100)
y = x + stats.norm.rvs(0, 1, size=100)
mean_x, mean_y = np.mean(x), np.mean(y)
plt.scatter(x,y,color="limegreen")
plt.plot(np.linspace(0., 10., 100), mean_y*np.ones(100), "g--")
plt.plot(mean_x*np.ones(100), np.linspace(np.min(y)-1., np.max(y)+1., 100), "g--")
plt.show()・実行結果
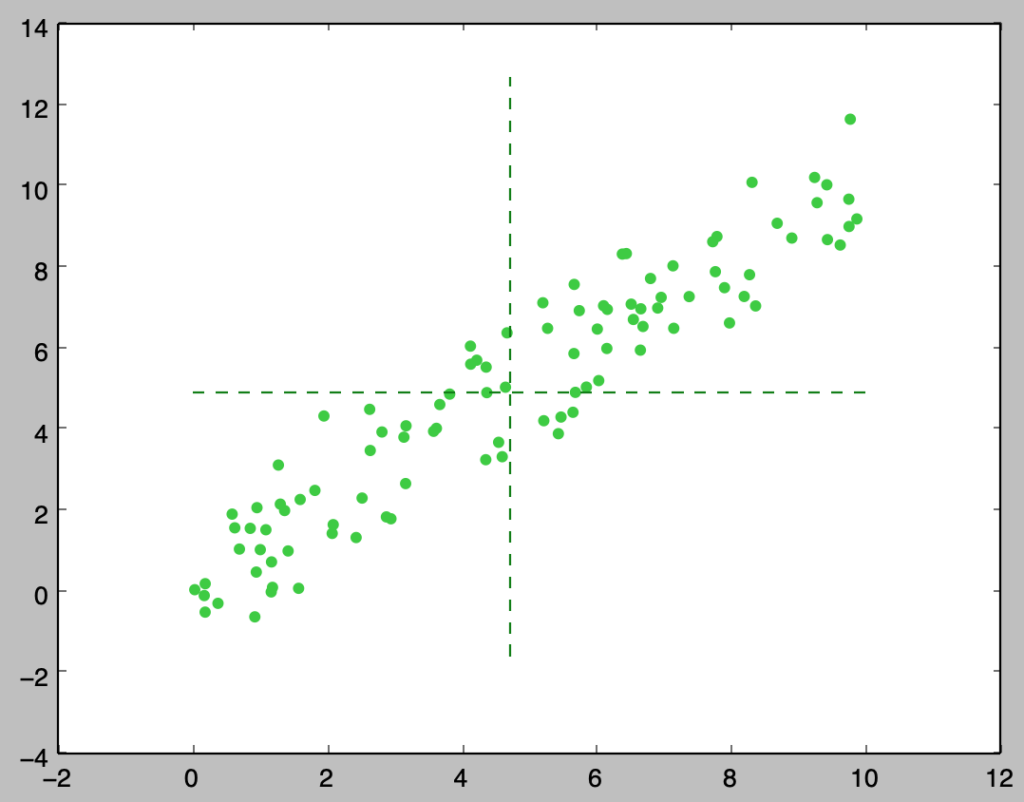
上記は正の相関がある観測値の散布図に直線$x=\bar{x}, y=\bar{y}$を書き入れたものです。上記より、正の相関がある場合は$(\bar{x},\bar{y})$の右上と左下にサンプルが多いことが確認できます。ここで共分散の式における$(x_i-\bar{x})(y_i-\bar{y})$は$(\bar{x},\bar{y})$の右上と左下に$(x_i,y_i)$があれば正、左上と右下に$(x_i,y_i)$があれば負の値を取ります。よって、共分散は$(x_i,y_i)$が$(\bar{x},\bar{y})$を基準にどの位置にあることが多いかを表す指標であると解釈できます。
相関係数の定義
共分散$s_{xy}$は$s_{xy}>0$であれば正の相関、$s_{xy}<0$であれば負の相関を表します。このとき相関の強さを判断するにあたっては、共分散は$x, y$のそれぞれの分散の値が大きくなるにつれて大きくなるのでスケールを調整する必要があります。
スケールの調整にあたって、相関係数$r_{xy}$を下記のように定義します。
$$
\large
\begin{align}
r_{xy} = \frac{s_{xy}}{s_x s_y}
\end{align}
$$
相関係数の解釈
相関係数を用いる際には下記の$3$点に注意すると良いです。
① 相関関係と因果関係は異なるので、因果関係を示す場合はそれぞれの変数の持つ意味を含めて考察する必要がある。
② 因果関係がなくても相関係数が大きい場合があり、このような場合を擬相関(spurious correlation)という。
③ 相関係数は$2$変数が線形式で表せる前提を置いているので非線形の関数で近似できる場合などは散布図などから判断する必要がある。
ベクトルの内積を用いた相関係数の表現
ベクトル$\mathbf{x}-\bar{\mathbf{x}}, \mathbf{y}-\bar{\mathbf{y}}$をそれぞれ下記のように定めます。
$$
\large
\begin{align}
\mathbf{x}-\bar{\mathbf{x}} &= \left( \begin{array}{c} x_1-\bar{x} \\ \vdots \\ x_n-\bar{x} \end{array} \right) \\
\mathbf{y}-\bar{\mathbf{y}} &= \left( \begin{array}{c} y_1-\bar{y} \\ \vdots \\ y_n-\bar{y} \end{array} \right)
\end{align}
$$
このとき相関係数は下記のように表すことができます。
$$
\large
\begin{align}
r_{xy} &= \frac{s_{xy}}{s_x s_y} \\
&= \frac{\displaystyle \sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sqrt{\sum_{i=1}^{n} (x_i-\bar{x})^2 \cdot \sum_{i=1}^{n} (y_i-\bar{y})^2}} \\
&= \frac{(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}})}{|\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}|}
\end{align}
$$
さらにここで下記が成立します。
$$
\large
\begin{align}
r_{xy} &= \frac{(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}})}{|\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}|} \\
(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}}) &= |\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}| r_{xy} \\
&= |\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}| \cos{\theta}
\end{align}
$$
上記では内積の定義に基づき$r_{xy}=\cos{\theta}$のように表しましたが、$\theta$はベクトル$\mathbf{x}-\bar{\mathbf{x}}, \mathbf{y}-\bar{\mathbf{y}}$のなす角であると解釈することができます。
