当記事は「白砂, 例題で学ぶ初歩からの統計学 第$2$版 (日本評論社)」の読解サポートにあたって$13$章「回帰分析」の練習問題を解説します。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。(そのため著者の意図とは異なる解説となる可能性はあります)
・統計学に関する書籍の解答集
https://www.hello-statisticians.com/answer_textbook
執筆:@kakusan96
Contents
回帰分析
回帰分析は2つ以上の変数間の因果関係を明らかにするための統計的手法である。特に3変数以上のケースは重回帰分析という。
2つの変数X, Yの関係を次の一次式に表すと
$Y = a + bX$
となり、Yを被説明変数、Xを説明変数、a、bを回帰係数という。この回帰係数を最小2乗法によって推定する。
Yの実測値をYとする。また、Y, a, bについて最小2乗法によって求めた推定値をそれぞれ$\hat{Y}$, $\hat{a}$, $\hat{b}$とする。
$\hat{Y} = \hat{a}X + \hat{b}$
実測値Yと推定値$\hat{Y}$の差をeとすると
$
\begin{align}
e &= Y – \hat{Y} \\
&= Y – (\hat{a} + \hat{b}X) \\
\sum e^2 &= \sum(Y – (\hat{a} + \hat{b}X))^2 \\
\end{align}
$
となる。この実測値Yと推定値$\hat{Y}$の差の2乗値(残差平方和)の総和$e^2$が最小になる回帰係数$\hat{a}$、$\hat{b}$を求めるのが最小2乗法である。最小値を求めるには上記の式を$\hat{a}$、$\hat{b}$でそれぞれ偏微分して0とおく。
$
\begin{align}
&\frac{d}{d\hat{a}}(\sum e^2) = 0 \\
&\frac{d}{da}(\sum(Y – (\hat{a} + \hat{b}X))^2) = 0\\
&\sum (2X^2\hat{a} – 2XY +2\hat{b}X)= 0\\
&2\hat{a}\sum X^2 – 2\sum XY +2\hat{b} \sum X= 0\\
&\hat{a}\sum X^2 – \sum XY +\hat{b} \sum X= 0\\
\end{align}
$
$
\begin{align}
&\frac{d}{d\hat{b}}(\sum e^2) = 0\\
&\frac{d}{db}(\sum(Y – (\hat{a}X + \hat{b}))^2) = 0\\
&\sum (2\hat{b} – 2Y +2\hat{a}X)= 0\\
&2\sum\hat{b} -2 \sum Y + 2\hat{a} \sum X = 0\\
&n\hat{b} – \sum Y + \hat{a} \sum X = 0\\
\end{align}
$
上記の二つの式を$\hat{a},\hat{b}$について連立方程式で解くと、
$
\begin{align}
\hat{b} &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2}\\
&= \frac{\sum (X- \bar{X})(Y- \bar{Y})}{\sum(X-\bar{X})^2}\\
&= \frac{\frac{1}{n-1}\sum (X- \bar{X})(Y- \bar{Y})}{\frac{1}{n-1}\sum(X-\bar{X})^2}\\
&=\frac{XとYの標本共分散}{Xの共分散} \\
\hat{a} &= \bar{Y} – \hat{b} \bar{X}
\end{align}
$
決定係数は推定した回帰式の当てはまりの良さを測る指標であり$r^2$とおくと、$0 \leq r^2 \leq 1$をとる。1に近いほど回帰式は当てはまりが良い。また相関係数の2乗である。
観測値Yと観測値の平均$\bar{Y}$の差の平方和をYの全変動という。
推定値$\hat{Y}$と観測値の平均$\bar{Y}$の差の平方和をYの回帰平方和という。
観測値Yと推定値$\hat{Y}$の差の平方和をYの残差平方和という。
これら3つの式には以下のような関係が成り立つ。
$
\sum(Y-\bar{Y})^2 = \sum(\hat{Y}-\bar{Y})^2 + \sum(Y-\hat{Y})^2
$
上記の式の両辺を$\sum(Y-\bar{Y})^2$で割ると
$
\begin{align}
1 &= \frac{\sum(\hat{Y}-\bar{Y})^2}{\sum(Y-\bar{Y})^2} + \frac{\sum(Y-\hat{Y})^2}{\sum(Y-\bar{Y})^2}\\
\frac{\sum(\hat{Y}-\bar{Y})^2}{\sum(Y-\bar{Y})^2} &= 1 – \frac{\sum(Y-\hat{Y})^2}{\sum(Y-\bar{Y})^2}\\
\end{align}
$
つまり、決定係数とは回帰平方和(回帰によって説明できるYの変動)をYの全変動で割った値である。
なお、実際に計算するときは、上記の式を変形して、
$
\begin{align}
r^2 &= \frac{(\sum(X-\bar{X})(Y-\bar{Y}))^2}{\sum (X-\bar{X})^2 \sum (Y-\bar{Y})^2}\\
r^2 &= \frac{(n\sum XY-(\sum X)(\sum Y))^2}{(n\sum X^2-(\sum X)^2)(n\sum Y^2-(\sum Y)^2)}
\end{align}
$
を用いて計算する。
演習問題 解答例
13-1. 単純回帰分析
①
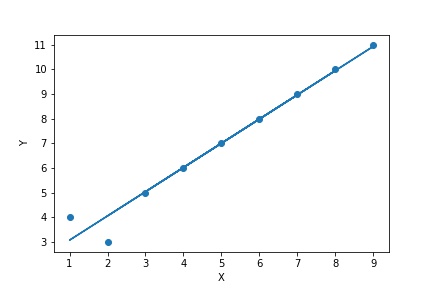
②
求める回帰係数を$Y = \hat{a} + \hat{b}X$とすると
$
\begin{align}
&\sum X = 45 \\
&\sum Y = 63 \\
&\sum X^2 = 285 \\
&\sum Y^2 = 501 \\
&\sum XY = 374 \\
&n = 9
\end{align}
$
であるため、
$
\begin{align}
\hat{b} &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2} \\
\hat{a} &= \bar{Y} – \hat{b} \bar{X} \\
\end{align}
$
に当てはめると
$
\begin{align}
\hat{b} &= \frac{(9) (374) -(45)(63)}{(9) (285) – (45)^2} \\
&= \frac{531}{540} \\
&= 0.983 \\
\end{align}
$
$
\begin{align}
\hat{a} &= \frac{\sum Y}{n} – \hat{b} \cdot \frac{\sum X}{n} \\
&= \frac{63}{9} – 0.983 \cdot \frac{45}{9} \\
&= 2.08
\end{align}
$
よって求める回帰式は$Y = 2.08 + 0.983X$である。
③
①を参照
④
$r^2 = \frac{(n\sum XY-(\sum X)(\sum Y))^2}{(n\sum X^2-(\sum X)^2)(n\sum Y^2-(\sum Y)^2)}$に当てはめると
$
\begin{align}
r^2 &= \frac{((9)(374)-(45)(63))^2}{((9)(285)-(45)^2)((9)(501)-(63)^2)}\\
&= \frac{281961}{291600}\\
&= 0.967
\end{align}
$
であり、当てはまりの良い回帰式であるといえる。
13-2. 単純回帰分析
求める回帰係数を$Y = \hat{a} + \hat{b}X$とすると
$
\begin{align}
&\sum X = 40\\
&\sum Y = 32\\
&\sum X^2 = 260\\
&\sum XY = 110\\
&n = 8\\
\end{align}
$
であるため、
$
\begin{align}
\hat{b} &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2}\\
\hat{a} &= \bar{Y} – \hat{b} \bar{X}\\
\end{align}
$
に当てはめると
$
\begin{align}
\hat{b} &= \frac{(8) (110) -(40)(32)}{(8) (260) – (40)^2}\\
&= \frac{-400}{480}\\
&= -0.833\\
\hat{a} &= \frac{\sum Y}{n} – \hat{b} \cdot \frac{\sum X}{n} \\
&= \frac{32}{8} -0.833 \cdot \frac{40}{8} \\
&= 8.17\\
\end{align}
$
よって求める回帰式は$Y = 8.17 -0.833X$である。
12-1より相関係数 $r=-0.973$ より決定係数 $r^2$ は $r^2 = (-0.973)^2=0.947$ である。
13-3. 単純回帰分析
求める回帰係数を$Y = \hat{a} + \hat{b}X$とすると
$
\begin{align}
&\sum X = 60 \\
&\sum Y = 50 \\
&\sum X^2 = 366.68 \\
&\sum XY = 302.23 \\
&n = 10
\end{align}
$
であるため、
$
\begin{align}
\hat{b} &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2} \\
\hat{a} &= \bar{Y} – \hat{b} \bar{X}
\end{align}
$
に当てはめると
$
\begin{align}
\hat{b} &= \frac{10) (302.23) -(60)(50)}{(10) (366.68) – (60)^2} \\
&= \frac{22.3}{66.8} \\
&= 0.3338 \\
\hat{a} &= \frac{\sum Y}{n} – \hat{b} \cdot \frac{\sum X}{n} \\
&= \frac{50}{10} – 0.3338 \cdot \frac{60}{10} \\
&= 2.997
\end{align}
$
よって求める回帰式は$Y = 2.997 + 0.3338X$である。
12-2より相関係数$r=0.9414$より決定係数$r^2$は$r^2 = (0.9414)^2 = 0.8862$である。
13-4. 単純回帰分析
求める回帰係数を$Y = \hat{a} + \hat{b}X$とすると
$
\begin{align}
&\sum X = 180\\
&\sum Y = 2100\\
&\sum X^2 = 2456\\
&\sum XY = 26015\\
&n = 15
\end{align}
$
であるため、
$
\begin{align}
\hat{b} &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2}\\
\hat{a} &= \bar{Y} – \hat{b} \bar{X}
\end{align}
$
に当てはめると
$
\begin{align}
\hat{b} &= \frac{(15) (26015) -(180)(2100)}{(15) (2456) – (180)^2}\\
&= \frac{12225}{4440}\\
&= 2.753\\
\hat{a} &= \frac{\sum Y}{n} – \hat{b} \cdot \frac{\sum X}{n} \\
&= \frac{2100}{15} – 2.753 \cdot \frac{180}{15} \\
&= 107.0
\end{align}
$
よって求める回帰式は$Y = 107.0 + 2.753X$である。
12-3より相関係数$r = 0.8930$より決定係数$r^2$は$r^2 = (0.8930)^2 = 0.7974$である。
13-5. 単純回帰分析の応用:変数の変換
①
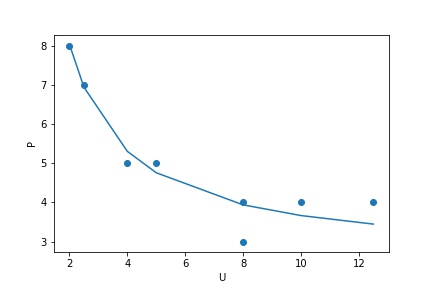
②
求めるフィリップス曲線について$Y = P, X = \frac{1}{U}$とおくと、$Y = a + bX$として最小二乗法によって回帰係数$a, b$を求める。
$
\begin{align}
&\sum X = 1.78\\
&\sum Y = 40\\
&\sum X^2 = 0.56015\\
&\sum Y^2 = 220\\
&\sum XY = 10.69\\
&n = 8\\
\end{align}
$
であるため、
$
\begin{align}
b &= \frac{n \sum XY -(\sum X)(\sum Y)}{n \sum X^2 – (\sum X)^2}\\
a &= \bar{Y} – b \bar{X}
\end{align}
$
に当てはめると
$
\begin{align}
b &= \frac{(8) (10.69) -(1.78)(40)}{(8) (0.5615) – (1.768)^2}\\
&= \frac{14.32}{1.3128}\\
&= 10.91\\
a &= \frac{\sum Y}{n} – b \cdot \frac{\sum X}{n} \\
&= \frac{40}{8} – 10.91 \cdot \frac{1.78}{8} \\
&= 2.573
\end{align}
$
よって仮定した回帰式は$Y = 2.573 + 10.91X$である。
求めるフィリップス曲線は$P = 2.573 + 10.91\frac{1}{U}$である。
決定係数は
$r^2 = \frac{(n\sum XY-(\sum X)(\sum Y))^2}{(n\sum X^2-(\sum X)^2)(n\sum Y^2-(\sum Y)^2)}$ に当てはめると
$
\begin{align}
r^2 &= \frac{((8)(10.69)-(1.78)(40))^2}{((8)(0.56015)-(1.78)^2)((8)(220)-(40)^2)}\\
&= 0.9763
\end{align}
$
③
①を参照。
13-6. 単純回帰分析の応用:変数の対数変換
①
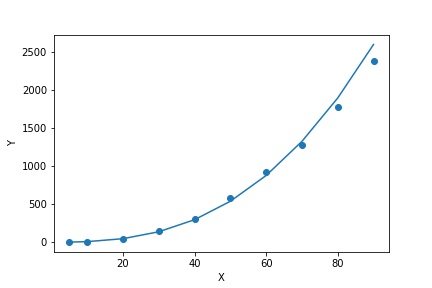
②
指数関数$Y = aX^b$を対数変換すると
$
\begin{align}
\log Y &= \log aX^b\\
&= \log a + \log X^b\\
&= \log a + b \log X\\
\end{align}
$
となり、
$
\begin{align}
y &= \log Y\\
x &= \log X\\
a &= \log a \\
\end{align}
$
とおくと$Y = aX^b$は$y=a + bx$と変換できる。最小二乗法にてこの回帰係数$a, b$を求める。
$
\begin{align}
&\sum x= 35.13453\\
&\sum y = 52.16806\\
&\sum x^2 = 131.61032\\
&\sum y^2 = 330.86730\\
&\sum xy = 205.17888\\
&n = 10
\end{align}
$
であるため、
$
\begin{align}
b &= \frac{n \sum xy -(\sum x)(\sum y)}{n \sum x^2 – (\sum x)^2}\\
a &= \bar{y} – \hat{b} \bar{x}
\end{align}
$
に当てはめると
$
\begin{align}
b &= \frac{(10) (205.17888) -(35.13453)(52.16806)}{(10) (131.61032) – (35.13453)^2}\\
&= 2.6801\\
a &= \frac{\sum y}{n} – b \cdot \frac{\sum x}{n} \\
&= \frac{52.16806}{10} – 2.6801 \cdot \frac{35.13453}{10} \\
&= -4.2001
\end{align}
$
よって仮定した回帰式は$y = -4.2001 + 2.6801x$である。
$
\begin{align}
&\log Y = y\\
&\log X = x\\
&\log a = -4.2001
\end{align}
$
より
$
\begin{align}
a &= e^{-4.2001} = 0.01499 (\log a = -4.2001)\\
Y &= aX^b\\
&= 0.01499X^{2.6801}
\end{align}
$
よって求める指数関数は$Y = 0.01499X^{2.6801}$である。
決定係数は
$
r^2 = \frac{(n\sum XY-(\sum X)(\sum Y))^2}{(n\sum X^2-(\sum X)^2)(n\sum Y^2-(\sum Y)^2)}
$
に当てはめると
$
\begin{align}
r^2 &= \frac{((10)(205.17888)-(35.13453)(52.16806))^2}{((10)(131.61032)-(35.13453)^2)((10)(330.86730)-(52.16806)^2)}\\
&= 0.9992
\end{align}
$
③
①を参照。
13-7. 単純回帰分析の応用:変数の対数変換
①
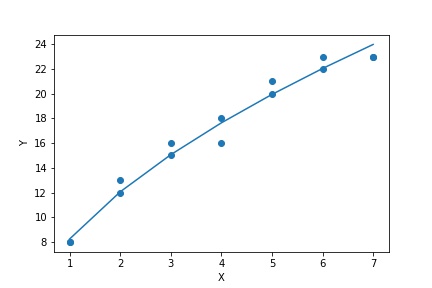
②
指数関数$Y = aX^b$を対数変換すると
$
\begin{align}
\log Y &= \log aX^b\\
&= \log a + \log X^b\\
&= \log a + b \log X
\end{align}
$
となり、
$
\begin{align}
&y = \log Y\\
&x = \log X\\
&a = \log a
\end{align}
$
とおくと$Y = aX^bはy=a + bx$と変換できる。
最小二乗法にてこの回帰係数a, bを求める。
$
\begin{align}
&\sum x= 17.05032\\
&\sum y = 38.89012\\
&\sum x^2 = 26.39295\\
&\sum y^2 = 109.75621\\
&\sum xy = 50.45257\\
&n = 14
\end{align}
$
であるため、
$
\begin{align}
b &= \frac{n \sum xy -(\sum x)(\sum y)}{n \sum x^2 – (\sum x)^2}\\
a &= \bar{y} – \hat{b} \bar{x}
\end{align}
$
に当てはめると
$
\begin{align}
b &= \frac{(14) (50.45257) -(17.05032)(38.89012)}{(14) (26.39295) – (17.05032)^2}\\
&= 0.54890\\
a &= \frac{\sum y}{n} – b \cdot \frac{\sum x}{n} \\
&= \frac{38.89012}{10} – 0.54890 \cdot \frac{17.05032}{10} \\
&= 2.1094
\end{align}
$
よって仮定した回帰式は$y = 2.1094 + 0.54890x$である。
$
\begin{align}
&\log Y = y\\
&\log X = x\\
&\log a = a
\end{align}
$
より
$
\begin{align}
a &= e^{21094} = 8.243, (\log a = 2.1094)\\
Y &= aX^b\\
&= 8.243X^{0.54890}
\end{align}
$
よって求める指数関数は$Y = 8.243X^{0.54890}$である。
決定係数は
$
r^2 = \frac{(n\sum XY-(\sum X)(\sum Y))^2}{(n\sum X^2-(\sum X)^2)(n\sum Y^2-(\sum Y)^2)}
$
に当てはめると
$
\begin{align}
r^2 &= \frac{((14)(50.45257)-(17.05032)(38.89012))^2}{((14)(26.39295)-(17.05032)^2)((14)(109.7562)-(38.89012)^2)}\\
&= 0.983138
\end{align}
$
③
①を参照。
13-8. 重回帰分析
重回帰分析は説明変数が二つ以上ある回帰分析である。被説明変数Yが二つの説明変数$X_1$, $X_2$によって説明される重回帰式を以下のように表す。
$
Y = \hat{a} + \hat{b_1}X_1 + \hat{b_2}X_2
$
先に学んだ最小二乗法にてパラメータ$a, b_1, b_2$を推定する。
$
\sum e^2 = \sum(Y – \hat{a} – \hat{b_1}X – \hat{b_2}X) ^2
$
残差平方和$\sum e^2$が最小になるように、推定値$\hat{a}, \hat{b_1}, \hat{b_2}$を求める。
(1)以下の値を求める。
$
\begin{align}
&\sum X_1 \\
&\sum X_2\\
&\sum Y\\
&\sum X_1^2\\
&\sum X_2^2\\
&\sum Y^2\\
&\sum X_1Y\\
&\sum X_2Y\\
&\sum X_1X_2\\
\end{align}
$
(2)(1)より以下の値を求める。
$
\begin{align}
&S_{YY} = \sum (Y – \bar{Y})^2\\
&S_{11} = \sum (X_1 – \bar{X_1})^2\\
&S_{22} = \sum (X_2 – \bar{X_2})^2\\
&S_{Y1} = \sum (Y – \bar{Y})(X_1 – \bar{X_1})\\
&S_{Y2} = \sum (Y – \bar{Y})(X_2 – \bar{X_2})\\
&S_{12} = \sum (X_1 – \bar{X_1})(X_2 – \bar{X_2})
\end{align}
$
(3)(2)より以下の値を求める。
$
\begin{align}
D_0 &= S_{11}S_{22} – S_{12}^2\\
D_1 &= S_{Y1}S_{22} – S_{Y2}S_{12}\\
D_2 &= S_{Y2}S_{11} – S_{Y1}S_{12}
\end{align}
$
(4)(3)より以下の値を求める。
$
\begin{align}
&\hat{b_1} = \frac{D_1}{D_0}\\
&\hat{b_2} = \frac{D_2}{D_0}\\
&\hat{a} = \bar{Y} – \hat{b_1} \bar{X_1} – \hat{b_2} \bar{X_2}
\end{align}
$
$\hat{b_1}$は$X_1$以外の説明変数が一定の時、$X_1$の変化によって生じるYの変化を表し、$\hat{b_2}$は$X_2$以外の説明変数が一定の場合$X_2$の変化によって生じるYの変化を表す。
重回帰分析における決定係数$r^2$は単回帰分析の決定係数と同様に回帰平方和(回帰によって説明できるYの変動)をYの全変動で割った値である。
$
\begin{align}
r^2 &= \frac{\sum (\hat{Y} – \bar{Y})}{\sum (Y – \bar{Y})}\\
&= \frac{\hat{b_1}S_{Y1} + \hat{b_2}S_{Y2}}{S_{YY}}
\end{align}
$
となる。
ただし、重回帰係数の決定係数$r^2$は説明変数の値を増やしていくとその値が自動的に大きくなってしまう。説明力を持たない説明変数でも、モデルに追加することで残差が小さくなることがあるためである。その問題を解決するためにサンプルサイズを$n$, 説明変数の数を$k$とおいて、自由度修正済み決定係数$\bar{r^2}$を以下の式にて求める。
$
\bar{r^2} = 1 – \frac{n-1}{n-k-1}(1-r^2)
$
13-9. 重回帰分析
①
求める回帰式を$\hat{Y} = \hat{a} + \hat{b_1}X_1 + \hat{b_2}X_2$とする。
以下の値を求める。
$
\begin{align}
&\sum X_1 = 40\\
&\sum X_2 = 50\\
&\sum Y = 700\\
&\sum X_1^2 = 196\\
&\sum X_2^2 = 308\\
&\sum Y^2 = 62400\\
&\sum X_1Y = 2150\\
&\sum X_2Y = 2790\\
&\sum X_1X_2 = 226\\
&n = 10
\end{align}
$
(1)より以下の値を求める。
$
\begin{align}
&S_{YY} = 13400\\
&S_{11} = 36\\
&S_{22} = 58\\
&S_{Y1} = -650\\
&S_{Y2} = -710\\
&S_{12} = 26\\
\end{align}
$
(2)より以下の値を求める。
$
\begin{align}
D_0 &= 1412\\
D_1 &= -19240\\
D_2 &= -8660
\end{align}
$
(3)より以下の値を求める。
$
\begin{align}
\hat{b_1} &= -13.63\\
\hat{b_2} &= -6.133\\
\hat{a} &= 155.2
\end{align}
$
よって求める回帰方程式は$\hat{Y} = 155.2 -13.63X_1 -6.133X_2$である。
②
決定係数$r^2 = \frac{\hat{b_1}S_{Y1} + \hat{b_2}S_{Y2}}{S_{YY}}$に当てはめると
$
\begin{align}
r^2 &= \frac{(-13.63)(-650) + (-6.133)(-710)}{13400}\\
&= 0.9859
\end{align}
$
自由度修正済み決定係数$\bar{r^2}$
$\bar{r^2} = 1 – \frac{n-1}{n-k-1}(1-r^2)$ に当てはめると
$
\begin{align}
\bar{r^2} &= 1 – \frac{10-1}{10-2-1}(1-0.9859)\\
&= 0.9819
\end{align}
$
③
$\hat{Y} = 155.2 – 13.63X_1 – 6.133X_2$より中古車価格は136,300円低下する。
④
$\hat{Y} = 155.2 – 13.63X_1 – 6.133X_2$より中古車価格は61,330円低下する。
⑤
$\hat{Y} = 155.2 – 13.63X_1 – 6.133X_2$より$155.2 -13.63(3) – 6.133(7) = 71.4$
よって、約71.4万円である。
13-10. 重回帰分析の応用:2次関数の推定
①
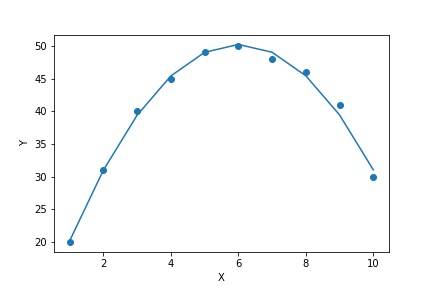
②
$X = X_1, X^2 = X_2$とおくと、求める回帰式を$\hat{Y} = \hat{a} + \hat{b_1}X_1 + \hat{b_2}X_2$とする。
以下の値を求める。
$
\begin{align}
&\sum X_1 = 55\\
&\sum X_2 = 385\\
&\sum Y = 400\\
&\sum X_1^2 = 385\\
&\sum X_2^2 = 25333\\
&\sum Y^2 = 16888\\
&\sum X_1Y = 2300\\
&\sum X_2Y = 15866\\
&\sum X_1X_2 = 3025\\
&n = 10
\end{align}
$
(1)より以下の値を求める。
$
\begin{align}
&S_{YY} = 888\\
&S_{11} = 82.5\\
&S_{22} = 10510.5\\
&S_{Y1} = 100\\
&S_{Y2} = 466\\
&S_{12} = 907.5
\end{align}
$
(2)より以下の値を求める。
$
\begin{align}
D_0 &= 43560.0\\
D_1 &= 628155.0\\
D_2 &= -52305.0
\end{align}
$
(3)より以下の値を求める。
$
\begin{align}
\hat{b_1} &= 14.4205\\
\hat{b_2} &= -1.20076\\
\hat{a} &= 6.91667
\end{align}
$
よって求める回帰方程式は$\hat{Y} = 6.91667 -14.4205X – 1.20076X^2$である。
③
決定係数$r^2 = \frac{\hat{b_1}S_{Y1} + \hat{b_2}S_{Y2}}{S_{YY}}$に当てはめると
$
\begin{align}
r^2 &= \frac{(-14.4205)(100) + (-1.20076)(466)}{888}\\
&= 0.9938
\end{align}
$
④
① を参照
⑤
$\hat{Y} = 6.91667 -14.4205X – 1.20076X^2$より、$6.91667 -14.4205(4.5) – 1.20076(4.5)^2 = 47.49$であるため、求める収穫量は47.49kg/aである。
⑥
$\hat{Y} = 6.91667 -14.4205X – 1.20076X^2$より、$6.91667 -14.4205(0) – 1.20076(0)^2 = 6.91667$であるため、求める収穫量は6.91667kg/aである。
⑦
最大値は$a – \frac{\hat{b_1}^2}{4\hat{b}_2} = 50.21236$、最大値になる肥料使用量は$\frac{-b_1}{2 \cdot b_2} = 6.00474$。
よって、約$6kg/a$の時に最大値約$50.21236kg/a$をとる。
13-11. 単純回帰分析:統計解析ソフトウェア使用
①
統計解析ソフトウェアを用いて計算すると $\hat{Y} = -43.749 + 0.36041X_1 + 0.63365X_2 + 1.0587X_3$
②
$
\begin{align}
r^2 = 0.99736 \\
\bar{r^2} = 0.99637
\end{align}
$
③
$\hat{b_1} = 0.36041$より、約3604円増加する。
④
$\hat{b_2} = 0.63365$より、約6337円増加する。
⑤
$\hat{b_3} = 1.0587$より、約1,0587円増加する。
⑥
M:$\hat{Y} = -43.749 + 0.36041(165) + 0.63365(60) + 1.0587(26)$より約81,2600円
N:$\hat{Y} = -43.749 + 0.36041(190) + 0.63365(48) + 1.0587(32)$より約890,200円
O:$\hat{Y} = -43.749 + 0.36041(125) + 0.63365(52) + 1.0587(27)$より約628,400円
P:$\hat{Y} = -43.749 + 0.36041(105) + 0.63365(39) + 1.0587(35)$より約558,600円
Q:$\hat{Y} = -43.749 + 0.36041(200) + 0.63365(57) + 1.0587(13)$より約782,100円




