あつまれ統計の森

Hello Statisticians!

ブログ

行列の固有多項式とケーリー・ハミルトンの定理(Cayley–Hamilton theorem)

投稿日: 投稿者: lib-arts

ケーリー・ハミルトンの定理(Cayley–Hamilton theorem)は行列の次数下げなどにあたって用いられる式です。当記事では行列の固有多項式に基づくケーリー・ハミルトンの定理の一般的な式を確認した後に、$2$次正方行列のケーリー・ハミルトンの定理の式との対応について確認します。
作成にあたっては「チャート式シリーズ 大学教養 線形代数」の第$8$章「固有値問題と行列の対角化」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 線形代数 (チャート式・シリーズ)

チャート式シリーズ 大学教養 線形代数 (チャート式・シリーズ)

3,080円(10/26 14:32時点)
Amazon

前提の確認

行列の固有多項式

$n$次正方行列$A$の変数$t$の固有多項式$F_{A}(t)$は行列式$\det$と$n$次の単位行列$I_{n}$を元に下記のように定義される。
$$
\large
\begin{align}
F_{A}(t) = \det{(tI_{n} – A)}
\end{align}
$$

$2$次正方行列におけるケーリー・ハミルトンの定理

$$
\large
\begin{align}
A = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)
\end{align}
$$

上記のように定義される$2$次正方行列$A$について下記が成立する。
$$
\large
\begin{align}
A^{2} – (a+d)A + (ad – bc) I_{2} &= O \\
A^{2} &= (a+d)A – (ad – bc) I_{2} \quad (1)
\end{align}
$$

上記の$O$は零行列を表す。

ケーリー・ハミルトンの定理

固有多項式とケーリー・ハミルトンの定理

$n$次正方行列$A$の固有多項式が$F_{A}(t)$のように表されるとき、下記が成立する。
$$
\large
\begin{align}
F_{A}(A) = O
\end{align}
$$

上記をケイリー・ハミルトンの定理という。

$2$次正方行列の式の導出

$$
\large
\begin{align}
A = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)
\end{align}
$$

上記のように定義される$2$次正方行列$A$の固有多項式$F_{A}(t)$は下記のように表すことができる。
$$
\large
\begin{align}
F_{A}(t) &= \det{(tI_{n} – A)} \\
&= \left| \begin{array}{cc} t-a & b \\ c & t-d \end{array} \right| \\
&= (t-a)(t-d) – bc \\
&= t^{2} -(a+d)t + ad-bc
\end{align}
$$

上記より、$F_{A}(A)=O$は下記のように変形できる。
$$
\large
\begin{align}
F_{A}(A) &= O \\
A^{2} -(a+d)A + (ad-bc)I_{2} &= O \\
A^{2} &= (a+d)A – (ad-bc)I_{2} \quad (2)
\end{align}
$$

$(2)$式は$(1)$式に一致する。

拡散モデルのlossの導出②：正規分布のKLダイバージェンスの計算に基づくlossの導出

投稿日: 投稿者: lib-arts

拡散とDenoisingに基づく拡散モデル(Diffision Model)は多くの生成モデル(generative model)に導入される概念です。当記事では正規分布のKLダイバージェンス(KL-Divergence)の計算を元にDDPM論文におけるlossの導出について取り扱いました。
Diffusion Model論文・DDPM論文や「拡散モデル ーデータ生成技術の数理(岩波書店)」の$2$章の「拡散モデル」などを参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

拡散モデル　データ生成技術の数理

拡散モデル　データ生成技術の数理

岡野原 大輔
3,520円(10/26 14:38時点)
発売日: 2023/02/17
Amazon

前提の確認

DDPM論文$(5)$式

$$
\begin{align}
L &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ D_{KL}(q(\mathbf{x}_{T}|\mathbf{x}_{0})||p_{\theta}(\mathbf{x}_{T})) + \sum_{t>1} D_{KL}(q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})||p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}))) – \log{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})} \right] \quad (1.1) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ L_{T} + \sum_{t>1} L_{t-1} + L_{0} \right] \quad (1.1)’
\end{align}
$$

上記の$(1.1), \, (1.1)’$式がDDPM論文の$\mathrm{Eq}. \: (5)$に対応する。導出については下記で詳しく取り扱った。

拡散モデルのlossの導出①：イェンセンの不等式に基づく変分下限とKLダイバージェンスを用いた表記

$2$つの正規分布のKLダイバージェンスの計算

$2$つの確率分布$p(x)$と$q(x)$に関するKLダイバージェンス$D_{KL}(p||q)$は下記のように表される。
$$
\large
\begin{align}
D_{KL}(p||q) = – \log{ \frac{q(x)}{p(x)} }
\end{align}
$$

$2$つの正規分布$\mathcal{N}(\mu_{a}, \Sigma_{a})$と$\mathcal{N}(\mu_{b}, \Sigma_{b})$のKLダイバージェンス$D_{KL}(\mathcal{N}(\mu_{a}, \Sigma_{a})||\mathcal{N}(\mu_{b}, \Sigma_{b}))$は$(1.2)$式より下記を用いて計算できる。
$$
\begin{align}
D_{KL}(\mathcal{N}(\mu_{a}, \Sigma_{a})||\mathcal{N}(\mu_{b}, \Sigma_{b})) &= \frac{1}{2} \left[ \log{ \frac{|\Sigma_{b}|}{|\Sigma_{a}|} } – d + \mathrm{tr} \left( \Sigma_{b}^{-1} \Sigma_{a} \right) + (\mu_{b}-\mu_{a})^{\mathrm{T}} \Sigma_{b}^{-1} (\mu_{b}-\mu_{a}) \right]
\end{align}
$$

拡散モデルのlossの導出

$q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})$の導出

$(1.1)$式の$q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})$は下記のように表される。
$$
\large
\begin{align}
q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}), \tilde{\beta}_{t} \mathbf{I}) \quad (2.1) \\
\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}) &= \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{\bar{\beta}_{t}} \mathbf{x}_{0} + \frac{\bar{\beta}_{t-1}}{\bar{\beta}_{t}} \mathbf{x}_{t} \quad (2.2) \\
\bar{\beta}_{t} &= \frac{\bar{\beta}_{t-1}}{\bar{\beta}_{t}} \beta_{t} \quad (2.3)
\end{align}
$$

$\displaystyle \small L_{t-1} = \mathbb{E}_{q} \left[ \frac{1}{2 \sigma_{t}^{2}} || \tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}) – \mu_{\theta}(\mathbf{x}_{t}, t) ||^{2} \right] + C$の導出

$\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0})$の詳細

以下、$\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0})$の詳細について式変形を元に確認を行う。まず、$(2.2)$式より$\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0})$は下記のように表される。
$$
\large
\begin{align}
\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}) = \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{\bar{\beta}_{t}} \mathbf{x}_{0} + \frac{\bar{\beta}_{t-1}}{\bar{\beta}_{t}} \mathbf{x}_{t} \quad (2.2)
\end{align}
$$

また、任意時刻の拡散条件付き確率の式$q(\mathbf{x}_{t}|\mathbf{x}_{0})$は下記のように表すことができる。
$$
\large
\begin{align}
q(\mathbf{x}_{t}|\mathbf{x}_{0}) &= \mathcal{N}(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}, (1 \, – \, \bar{\alpha}_{t}) \mathbf{I}) \quad (2.4) \\
\alpha_{t} &= 1-\beta_{t} \\
\bar{\alpha}_{t} &= \prod_{s=1}^{t} \alpha_{s}
\end{align}
$$

上記の導出は下記で詳しく取り扱った。

拡散モデル(Diffusion Model)の概要と式定義まとめ

$(2.4)$式より、$\mathbf{x}_{t}$は$\mathbf{x}_{0}$とノイズ$\epsilon$を用いて下記のように表せる。
$$
\large
\begin{align}
\mathbf{x}_{t}(\mathbf{x}_{0}, \epsilon) = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0} + \sqrt{1 \, – \, \bar{\alpha}_{t}} \epsilon, \quad \mathcal{N}(\mathbf{0}, \mathbf{I}) \quad (2.5)
\end{align}
$$

$(2.5)$式を$\mathbf{x}_{0}$について変形を行うと下記が得られる。
$$
\large
\begin{align}
\mathbf{x}_{0} = \frac{1}{\sqrt{\bar{\alpha}_{t}}} \left( \mathbf{x}_{t}(\mathbf{x}_{0}, \epsilon) \, – \, \sqrt{1 \, – \, \bar{\alpha}_{t}} \epsilon \right) \quad (2.6)
\end{align}
$$

ここで$(2.2)$式に$(2.6)$式を代入すると下記のように変形できる。
$$
\large
\begin{align}
\tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}) &= \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{\bar{\beta}_{t}} \mathbf{x}_{0} + \frac{\bar{\beta}_{t-1}}{\bar{\beta}_{t}} \mathbf{x}_{t} \quad (2.2) \\
&=
\end{align}
$$

$\mu_{\theta}(\mathbf{x}_{t}, t)$の詳細

$\displaystyle \small L_{t-1} = \mathbb{E}_{\mathbf{x}_{0}, \epsilon} \left[ \frac{\beta_{t}^{2}}{2 \sigma_{t}^{2} \alpha_{t} \bar{\beta}_{t}} \left| \middle| \epsilon – \epsilon_{\theta} \left( \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0} + \sqrt{\bar{\beta}_{t}} \epsilon, t \right) \middle| \right|^{2} \right] + C$の導出

DDPMを用いたサンプリング

拡散モデルのlossの導出①：イェンセンの不等式に基づく変分下限とKLダイバージェンスを用いた表記

投稿日: 投稿者: lib-arts

拡散とDenoisingに基づく拡散モデル(Diffision Model)は多くの生成モデル(generative model)に導入される概念です。当記事ではイェンセンの不等式(Jensen’s Inequality)やKLダイバージェンスの定義を用いた拡散モデルの負の対数尤度の変分下限の導出について取り扱いました。
Diffusion Model論文・DDPM論文や「拡散モデル ーデータ生成技術の数理(岩波書店)」の$2$章の「拡散モデル」などを参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

前提の確認

イェンセンの不等式

$$
\large
\begin{align}
\lambda_i & \geq 0 \\
\sum_{i=1}^{M} \lambda_{i} &= 1
\end{align}
$$

上記のように$\lambda_1, \cdots , \lambda_M$を定義するとき、下に凸の関数$f(x)$の任意の点$(x_i, f(x_i))$について下記の不等式が成立する。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{M} \lambda_{i} x_{i} \right) \leq \sum_{i=1}^{M} \lambda_{i} f \left( x_{i} \right) \quad (1.1)
\end{align}
$$

上記をイェンセンの不等式(Jensen’s Inequality)という。イェンセンの不等式については下記でも取り扱った。

イェンセンの不等式(Jensen’s inequality)と凸関数の期待値・凸集合まとめ

当記事で取り扱う導出で出てくる関数$f(x)=-\log{x}$が下に凸の関数であるので、当項では下に凸の関数についてのイェンセンの不等式を取り扱ったが、上に凸の関数についてのイェンセンの不等式は不等号が逆になることも合わせて抑えておくと良い。

期待値の定義式へのイェンセンの不等式の適用

前項$(1.1)$式の$\lambda_{i}$について$\displaystyle \lambda_i \geq 0, \, \sum_{i=1}^{M} \lambda_i = 1$が成立することから、$\lambda_{i}$に確率関数$p(x_i)$を対応させることができる。このとき下に凸の関数$f$について下記のような式が導出できる。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{M} p(x_i) x_{i} \right) & \leq \sum_{i=1}^{M} p(x_i) f \left( x_{i} \right) \\
f \left( \mathbb{E} \left[ x_{i} \right] \right) & \leq \mathbb{E} \left[ f \left( x_{i} \right) \right]
\end{align}
$$

上記は離散型確率分布の式から導出したが、連続変数についても同様に下記が成立する。
$$
\large
\begin{align}
f \left( \int x p(x) dx \right) & \leq \int f(x) p(x) dx
\end{align}
$$

KLダイバージェンスの定義と解釈

連続型確率分布$p(x)$と$q(x)$のKLダイバージェンス$\mathrm{KL}(p||q)$は下記のように定義される。
$$
\large
\begin{align}
\mathrm{KL}(p||q) &= -\int \left[ p(x) \log{\frac{q(x)}{p(x)}} \right] dx \\
&= -\int \left[ p(x) \log{q(x)} \, – \, p(x) \log{{p(x)}} \right] dx \\
&= \int \left[ p(x) \log{\frac{p(x)}{q(x)}} \right] dx \quad (1.2)
\end{align}
$$

上記の式は$p$に対応する確率分布の期待値の記号$\mathbb{E}_{p}$を用いて下記のように表すこともできる。
$$
\large
\begin{align}
\mathrm{KL}(p||q) &= \mathbb{E}_{p} \left[ – \log{\frac{q(x)}{p(x)}} \right] \quad (1.3)
\end{align}
$$

$(1.3)$式は離散型確率分布でも成立する。KLダイバージェンスの解釈にあたっては、確率分布$p(x)$と$q(x)$の類似度を表すと解釈すればよい。下記ではソフトマックス関数を題材にKLダイバージェンスの値の変化について具体的に取り扱った。

「一様分布」と「Softmax関数による確率化」間のKLダイバージェンスの計算

拡散モデルのlossの導出

DDPM論文$(3)$式の導出

$\mathbf{x}_{0}$は学習に用いるサンプルに対応するので、lossに用いるnegative log-likelihood関数の期待値$l$は下記のように表せる。
$$
\large
\begin{align}
l = \mathbb{E} \left[ -\log{p_{\theta}(\mathbf{x}_{0})} \right] \quad (2.1)
\end{align}
$$

ここで「拡散モデル(Diffusion Model)の概要と式定義まとめ」の$(1)$式より、$p_{\theta}(\mathbf{x}_{0})$は下記のように表せる。
$$
\large
\begin{align}
p_{\theta}(\mathbf{x}_{0}) = \int p_{\theta}(\mathbf{x}_{0:T}) \, d\mathbf{x}_{1:T}
\end{align}
$$

上記は同時確率分布に関する基本演算に基づいて下記のように変形できる。
$$
\large
\begin{align}
p_{\theta}(\mathbf{x}_{0}) &= \int p_{\theta}(\mathbf{x}_{0:T}) \, d\mathbf{x}_{1:T} \\
&= \int p_{\theta}(\mathbf{x}_{0:T}) \cdot \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \, d\mathbf{x}_{1:T} \\
&= \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \, d\mathbf{x}_{1:T} \\
&= \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot p_{\theta}(\mathbf{x}_{T}) \frac{p_{\theta}(\mathbf{x}_{0:(T-1)}|\mathbf{x}_{T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \, d\mathbf{x}_{1:T} \\
&= \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \, d\mathbf{x}_{1:T} \quad (2.2)
\end{align}
$$

$(2.1)$式に$(2.2)$式を代入することで下記が得られる。
$$
\large
\begin{align}
l &= \mathbb{E} \left[ -\log{p_{\theta}(\mathbf{x}_{0})} \right] \quad (2.1) \\
&= \int -\log{p_{\theta}(\mathbf{x}_{0})} d \mathbf{x}_{0} \\
&= \int -\log{ \left[ \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} d\mathbf{x}_{1:T} \right] } d \mathbf{x}_{0} \quad (2.3)
\end{align}
$$

ここで$(2.3)$式の確率関数$q(\mathbf{x}_{1:T}|\mathbf{x}_{0})$に着目しイェンセンの不等式を適用することで下記が得られる。
$$
\large
\begin{align}
l &= \int -\log{ \left[ \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} d\mathbf{x}_{1:T} \right] } d \mathbf{x}_{0} \quad (2.3) \\
& \leq \int q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) \cdot \left( -\log{ \left[ p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right] } \right) d \mathbf{x}_{0:T} \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \left( p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right) } \right] \quad (2.4) \\
\end{align}
$$

条件付き確率の期待値の式に基づいて$(2.4)$式は下記のように変形できる。
$$
\large
\begin{align}
l &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \left( p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right) } \right] \quad (2.4) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} } \right] \quad (2.5)
\end{align}
$$

また、$(2.4)$式を$\log$に着目することで下記のように和の形式で表すこともできる。
$$
\large
\begin{align}
l &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \left( p_{\theta}(\mathbf{x}_{T}) \prod_{t=1}^{T} \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right) } \right] \quad (2.4) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T})} \, – \, \sum_{t \geq 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} } \right] \quad (2.6)
\end{align}
$$

$(2.5)$式と$(2.6)$式より、DDPMの論文の$\mathrm{Eq}. \, (3)$が正しいことが確認できる。

DDPM論文$(5)$式の導出

$(2.5)$式、$(2.6)$式は$\mathbf{x}_{0}$の負の対数尤度の変分下限であり、この変分下限を$L$とおくと$L$は下記のように変形できる。
$$
\large
\begin{align}
L &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} } \right] \quad (2.5) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \sum_{t \geq 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} } \right] \quad (2.6) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} } \, – \, \log{ \frac{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})}{q(\mathbf{x}_{1}|\mathbf{x}_{0})} } \right] \quad (2.7)
\end{align}
$$

ここで$t>1$のとき$q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$はマルコフ連鎖の定義とベイズの定理に基づいて下記のように変形を行える。
$$
\large
\begin{align}
q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) &= \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{t})q(\mathbf{x}_{t})}{q(\mathbf{x}_{t-1})} \\
&= \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})q(\mathbf{x}_{t}|\mathbf{x}_{0})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})} \quad (2.8)
\end{align}
$$

$(2.8)$式を$(2.7)$式に代入すると下記が得られる。
$$
\begin{align}
L &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} } \, – \, \log{ \frac{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})}{q(\mathbf{x}_{1}|\mathbf{x}_{0})} } \right] \quad (2.7) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} \cdot \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} } \, – \, \log{ \frac{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})}{q(\mathbf{x}_{1}|\mathbf{x}_{0})} } \right] \quad (2.9)
\end{align}
$$

ここで$(2.9)$式の$\displaystyle \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} \cdot \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} }$について下記が成立する。
$$
\large
\begin{align}
& \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} \cdot \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} } \\
&= \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } + \sum_{t > 1} \log{ \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} } \\
&= \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } + \log{ \prod_{t > 1} \frac{q(\mathbf{x}_{t-1}|\mathbf{x}{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} } \\
&= \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } + \log{ \left[ \frac{q(\mathbf{x}_{1}|\mathbf{x}_{0}) \cdot \cancel{q(\mathbf{x}_{2}|\mathbf{x}_{0})} \cdots \cancel{q(\mathbf{x}_{T-1}|\mathbf{x}_{0})}}{\cancel{q(\mathbf{x}_{2}|\mathbf{x}_{0})} \cdots \cancel{q(\mathbf{x}_{T-1}|\mathbf{x}_{0})} \cdot q(\mathbf{x}_{T}|\mathbf{x}_{0})} \right] } \\
&= \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } + \log{ \frac{q(\mathbf{x}_{1}|\mathbf{x}_{0})}{q(\mathbf{x}_{T}|\mathbf{x}_{0})} } \quad (2.10)
\end{align}
$$

$(2.10)$式を$(2.9)$式に代入することで下記が得られる。
$$
\begin{align}
L &= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} \cdot \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{t}|\mathbf{x}_{0})} } \, – \, \log{ \frac{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})}{q(\mathbf{x}_{1}|\mathbf{x}_{0})} } \right] \quad (2.9) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{p_{\theta}(\mathbf{x}_{T}}) \, – \, \log{ \frac{\cancel{q(\mathbf{x}_{1}|\mathbf{x}_{0})}}{q(\mathbf{x}_{T}|\mathbf{x}_{0})} } \, – \, \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } \, – \, \log{ \frac{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})}{\cancel{q(\mathbf{x}_{1}|\mathbf{x}_{0})}} } \right] \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ -\log{ \frac{p_{\theta}(\mathbf{x}_{T})}{q(\mathbf{x}_{T}|\mathbf{x}_{0})} } – \sum_{t > 1} \log{ \frac{p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})} } – \log{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})} \right] \quad (2.11) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ D_{KL}(q(\mathbf{x}_{T}|\mathbf{x}_{0})||p_{\theta}(\mathbf{x}_{T})) + \sum_{t>1} D_{KL}(q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})||p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}))) – \log{p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1})} \right] \quad (2.12) \\
&= \mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ L_{T} + \sum_{t > 1} L_{t-1} + L_{0} \right] \quad (2.12)’
\end{align}
$$

機械学習・DeepLearning分野の論文読解に役に立つ論文著者索引

投稿日: 投稿者: lib-arts

論文の本文中では「oo et al., yyyy」のように先行研究を参照することが多いです。それぞれ「References」に具体的な論文を確認することができる一方で、都度確認するのは大変です。そこで当記事では論文の著者名から該当する研究を確認できるような索引の作成を行いました。

作成にあたってはよく引用される各分野の有名論文を中心にabc順でまとめました。厳密さではなく、「概ねこの論文が該当するだろう」を重視しているので、正確にはそれぞれの論文の「References」を確認してください。特に複数該当する場合は多くの場合「yyyya, yyyyb, $\cdots$」のように表記されます。

DeepLearning

CNN

著者名該当研究
He et al., 2015ResNet
Krizhevsky et al., 2012AlexNet
Simonyan et al., 2014VGGNet

RNN・Transformer・LLM

著者名該当研究
Brown et al., 2020GPT-3
Devlin et al., 2018BERT
Du et al., 2021GLaM
Hoffmann et al., 2022Chinchilla
Kitaev et al., 2020Reformer
Liu et al., 2019RoBERTa
Mikolov et al., 2013Word2vec
Radford et al., 2018GPT・GPT-2
Rae et al., 2021Gopher
Raffel et al., 2020T5
Smith et al., 2022Megatron–Turing NLG
Sutskever et al., 2014seq2seq
Thoppilan et al., 2022LaMDA
Vaswani et al., 2017Transformer
Yang et al.,XLNet

生成モデル

著者名該当研究
Goodfellow et al., 2014GAN: Generative Adversarial networks
Ho et al., 2020DDPM
Sohl-Dickstein et al., 2015Diffusion Model
Radford et al., 2021CLIP
Ramesh et al., 2021DALL-E

GNN

著者名該当研究
Battaglia et al., 2018Graph Network・Inductive Bias
Gilmer et al., 2017MPNN: Message Passing Neural Network
Wang et al., 2018NLNN: Non-Local Neural Network

点群・集合

著者名該当研究
Lee et al., 2019Set Transformer
Qi et al., 2017PointNet
Zaheer et al., 2017Deep sets

強化学習

強化学習×Transformer

著者名該当研究
Chen et al., 2021Decision Transformer

拡散モデル(Diffusion Model)の概要と式定義まとめ

投稿日: 投稿者: lib-arts

拡散とDenoisingに基づく拡散モデル(Diffision Model)は多くの生成モデル(generative model)に導入される概念です。当記事では拡散モデルの概要と式定義、イェンセンの不等式などを用いるloss関数の導出などについて取りまとめを行いました。
DDPM論文や「拡散モデル ーデータ生成技術の数理(岩波書店)」の$2$章の「拡散モデル」などを参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

拡散モデル　データ生成技術の数理

拡散モデル　データ生成技術の数理

岡野原 大輔
3,520円(10/26 14:38時点)
発売日: 2023/02/17
Amazon

拡散モデルの概要

DDPM論文 Figure$\, 2$

拡散モデルの概要は上図を元に理解すると良い。$\mathbf{x}_{0}$が画像、$\mathbf{x}_{T}$が$\mathbf{x}_{0}$と次元が同じ潜在変数を表す。また、図の$q$が拡散過程(diffusion process)、$p$が逆向き過程(reverse process)にそれぞれ対応する。

拡散モデルでは元データに対し、拡散過程を適用した結果を逆向き過程で復元できるように逆向き過程$p$の学習を行うことで、新たに潜在変数の$\mathbf{x}_{T}$が与えられた際に$\mathbf{x}_{0}$を計算し、生成を行うことができる。

拡散モデルの式定義

拡散過程と逆拡散過程の式定義

拡散モデル(Diffusion model)は潜在変数モデルであり、下記のような式で定義される。
$$
\large
\begin{align}
p_{\theta}(\mathbf{x}_{0}) = \int p_{\theta}(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \quad (1)
\end{align}
$$

$(1)$式は生成される画像の分布は同時分布$p_{\theta}(\mathbf{x}_{0:T})$を$\mathbf{x}_{1}, \cdots , \mathbf{x}_{T}$について積分し、周辺分布を得たと解釈すると良い。ここで式に出てくる同時分布$p_{\theta}(\mathbf{x}_{0:T})$は下記のように定義する。
$$
\large
\begin{align}
p_{\theta}(\mathbf{x}_{0:T}) &= p(\mathbf{x}_{T}) \prod_{t=1}^{T} p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}) \quad (2) \\
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}) &= \mathcal{N}(\boldsymbol{\mu}_{\theta}(\mathbf{x}_{t},t), \boldsymbol{\Sigma}_{\theta}(\mathbf{x}_{t}, t)) \quad (3) \\
p(\mathbf{x}_{T}) &= \mathcal{N}(\mathbf{0}, \mathbf{I})
\end{align}
$$

$(2)$式の同時確率分布の分解(factorization)ではマルコフ性(Markov Property)を仮定している。また、$(3)$式は前節における逆向き過程を表す。多次元正規分布の平均ベクトルと共分散行列はDeep Learningを用いて学習を行ったパラメータ$\theta$の関数から出力される値である。

拡散モデルの特徴は$p$で表される逆向き過程(reverse process)に対応する拡散過程(diffusion process)の$q$を定義することである。拡散過程$q$はvariance scheduleの$\beta_1, \cdots , \beta_{T}$を用いて下記のように定義される。
$$
\large
\begin{align}
q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) &= \prod_{t=1}^{T} q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \quad (4) \\
q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) &= \mathcal{N} \left( \sqrt{1-\beta_{t}} \mathbf{x}_{t}, \beta_{t} \mathbf{I} \right) \quad (5)
\end{align}
$$

任意時刻の拡散条件付き確率の証明

$$
\large
\begin{align}
q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) &= \prod_{t=1}^{T} q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \quad (4) \\
q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) &= \mathcal{N} \left( \sqrt{1-\beta_{t}} \mathbf{x}_{t-1}, \beta_{t} \mathbf{I} \right) \quad (5)
\end{align}
$$

拡散過程$q$が上記のように表される時、任意時刻$t$における拡散条件付き確率$q(\mathbf{x}_{t}|\mathbf{x}_{0})$は下記のように表される。
$$
\large
\begin{align}
q(\mathbf{x}_{t}|\mathbf{x}_{0}) &= \mathcal{N}(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}, (1 \, – \, \bar{\alpha}_{t}) \mathbf{I}) \quad (6) \\
\alpha_{t} &= 1-\beta_{t} \quad (7) \\
\bar{\alpha}_{t} &= \prod_{s=1}^{t} \alpha_{s} \quad (8)
\end{align}
$$

上記の$(6)$式はDDPM論文の$\mathrm{Eq}. \: (4)$に対応する。以下、数学的帰納法を用いて上記の証明を行う。

・$[1] \,$ $t=1$の時
$(7)$式と$(8)$式より下記が成立する。
$$
\large
\begin{align}
\sqrt{\bar{\alpha}_{1}} &= \sqrt{\alpha_{1}} = \sqrt{1-\beta_{1}} \\
1 \, – \, \bar{\alpha_{1}} &= 1 \, – \, \alpha_{1} = \beta_{1}
\end{align}
$$

上記より$t=1$の時$(6)$式は$(5)$式の定義式に一致するので$(6)$式は成立する。

・$[2] \,$ $t=k$で$(6)$式が成立する場合の$t=k+1$の時
$t=k$で$(6)$式が成立するとき、下記が成立する。
$$
\large
\begin{align}
q(\mathbf{x}_{k}|\mathbf{x}_{0}) = \mathcal{N}(\sqrt{\bar{\alpha}_{k}} \mathbf{x}_{0}, (1 \, – \, \bar{\alpha}_{k}) \mathbf{I}) \quad (6)’
\end{align}
$$

このとき$(6)’$式に基づいて$\mathbf{x}_{k}$は下記のように表せる。
$$
\large
\begin{align}
\mathbf{x}_{k} = \sqrt{\bar{\alpha}_{k}} \mathbf{x}_{0} + \sqrt{1 \, – \, \bar{\alpha}_{k}} \epsilon, \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \quad (9)
\end{align}
$$

ここで$(5)$式の$q$の定義式より、$q(\mathbf{x}_{k+1}|\mathbf{x}_{k})$は下記のように表される。
$$
\large
\begin{align}
q(\mathbf{x}_{k+1}|\mathbf{x}_{k}) = \mathcal{N} \left( \sqrt{1-\beta_{t+1}} \mathbf{x}_{t}, \beta_{t+1} \mathbf{I} \right) \quad (5)’
\end{align}
$$

ここで$(5)’$式と$(9)$式に基づいて$\mathbf{x}_{k+1}$は下記のように表せる。
$$
\large
\begin{align} \mathbf{x}_{k+1} &= \sqrt{1-\beta_{t+1}} \mathbf{x}_{t} + \sqrt{\beta_{t+1}} \epsilon, \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\
&= \sqrt{1-\beta_{t+1}} (\sqrt{\bar{\alpha}_{k}} \mathbf{x}_{0} + \sqrt{1 \, – \, \bar{\alpha}_{k}} \epsilon) + \sqrt{\beta_{t+1}} \epsilon \\
&= \sqrt{\alpha_{t+1}} (\sqrt{\bar{\alpha}_{k}} \mathbf{x}_{0} + \sqrt{1 \, – \, \bar{\alpha}_{k}} \epsilon) + \sqrt{\beta_{t+1}} \epsilon \\
&= \sqrt{\bar{\alpha}_{k+1}} \mathbf{x}_{0} + \sqrt{\alpha_{k+1}} \sqrt{1 \, – \, \bar{\alpha}_{k}} \epsilon + \sqrt{\beta_{t+1}} \epsilon \quad (10)
\end{align}
$$

$(10)$式より、$\mathbf{x}_{k+1}$の分散は$\mathbf{X}, \mathbf{Y} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$とする際の$\sqrt{\alpha_{k+1}} \sqrt{1 \, – \, \bar{\alpha}_{k}} \mathbf{X} + \sqrt{\beta_{t+1}} \mathbf{Y}$の分散に一致する。ここで正規分布の再生性より、$\sqrt{\alpha_{k+1}} \sqrt{1 \, – \, \bar{\alpha}_{k}} \mathbf{X} + \sqrt{\beta_{t+1}} \mathbf{Y}$の分散$\mathbf{\Sigma}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{\Sigma} &= (\sqrt{\alpha_{k+1}} \sqrt{1 \, – \, \bar{\alpha}_{k}})^{2} \mathbf{I} + (\sqrt{\beta_{t+1}})^{2} \mathbf{I} \\
&= \alpha_{k+1} (1 \, – \, \bar{\alpha}_{k}) \mathbf{I} + \beta_{t+1} \mathbf{I} \\
&= \left( \cancel{\alpha_{k+1}} – \bar{\alpha}_{k+1} + 1 – \cancel{\alpha_{k+1}} \right) \mathbf{I} = (1-\bar{\alpha}_{k+1}) \mathbf{I}
\end{align}
$$

$(10)$式と$(11)$式より$q(\mathbf{x}_{k+1}|\mathbf{x}_{0})$は下記のように表せる。
$$
\large
\begin{align}
q(\mathbf{x}_{k+1}|\mathbf{x}_{0}) = \mathcal{N} \left( \sqrt{\bar{\alpha}_{k+1}} \mathbf{x}_{0}, (1-\bar{\alpha}_{k+1}) \mathbf{I} \right) \quad (12)
\end{align}
$$

$(12)$式より、$t=k$で$(6)$式が成立する場合、$t=k+1$でも$(6)$式が成立することが確認できる。

$[1], \, [2]$より、数学的帰納法に基づいて$(6)$式が成立することが示される。

モーメント母関数を用いた正規分布の再生性の導出は下記で詳しく取り扱った。

確率分布の再生性とその導出（二項分布・ポアソン分布・正規分布）

最大内積探索(MIPS; Maximum Inner Product Search)まとめ

投稿日: 投稿者: lib-arts

Routing TransformerのようなContent-based Sparse Attentionでは最大内積探索(MIPS; Maximum Inner Product Search)と類似した処理が行われます。当記事では最大内積探索の概要やクラスタリングを用いた計算の効率化について取りまとめました。
「Clustering is efficient for approximate maximum inner product search.」などを参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

最大内積探索の問題設定

最大内積探索の立式

$n$個の$D$次元ベクトルの集合$\mathcal{X}$を$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}, \, \mathbf{x}_{i} \in \mathbb{R}^{D}$のように定義する。このとき$D$次元のクエリ$q \in \mathbb{R}^{D}$と集合$\mathcal{X}$の要素であるベクトル$\mathbf{x}_{i}$に関する最大内積探索問題(MIPS; Maximum Inner Product Search problem)は下記のように立式することができる。
$$
\large
\begin{align}
\mathrm{arg} \max_{i} q^{\mathrm{T}} \mathbf{x}_{i}
\end{align}
$$

同様に、内積の計算結果が上位$K$に含まれるベクトルを探すK-MIPS問題は下記のように立式される。
$$
\large
\begin{align}
\mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$

最近傍探索と一致する場合

最大内積探索(MIPS)問題は最近傍探索(NNS; Nearest Neighbor Search)と関連する。より厳密には「ベクトル$\mathbf{x}_{i} \in \mathbb{R}^{D}$が同じユークリッドノルム(Euclidean norm)を持つ場合」にMIPSとNNSが一致する。K-NNSの式はクエリ$q$とベクトル$\mathbf{x}_{i}$間のノルムに着目することで上記のように表すことができる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} ||q \, – \, \mathbf{x}_{i}||^{2} \quad (1.2)
\end{align}
$$

ここでクエリ$q$とベクトル$\mathbf{x}_{i}$のユークリッドノルムが定数$C_1, C_2$を用いて$||q||^{2}=C_1, \, ||\mathbf{x}_{i}||^{2}=C_2$のように表せるとき、$(1.2)$式は下記のように同値変形できる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} ||q \, – \, \mathbf{x}_{i}||^{2} &= \mathrm{argmin}_{i}^{(K)} (q \, – \, \mathbf{x}_{i})^{\mathrm{T}} (q \, – \, \mathbf{x}_{i}) \\
&= \mathrm{argmin}_{i}^{(K)} \left( ||q||^{2} \, – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} + ||\mathbf{x}_{i}||^{2} \right) \\
&= \mathrm{argmin}_{i}^{(K)} \left( C_1 \, – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} + C_2 \right) \\
&= \mathrm{argmin}_{i}^{(K)} \left( – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} \right) \\
&= \mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$

上記より、$\mathbf{x}_{i}$のノルムが同じ場合は「同一のクエリ$q$についてのK-MIPS問題がK-NNS問題に帰着する」ことが確認できる。

MCSSと一致する場合

最大内積探索(MIPS)問題は最大余弦類似度探索(MCSS; Maximum Cosine Similarity Search)とも関連する。NNSと同様に厳密には「ベクトル$\mathbf{x}_{i} \in \mathbb{R}^{D}$が同じユークリッドノルム(Euclidean norm)を持つ場合」にMIPSとMCSSSが一致する。K-MCSSの式はクエリ$q$とベクトル$\mathbf{x}_{i}$間のノルムに着目することで上記のように表すことができる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{||q|| ||\mathbf{x}_{i}||} \quad (1.3)
\end{align}
$$

ここでクエリ$q$とベクトル$\mathbf{x}_{i}$のユークリッドノルムが定数$C_1, C_2$を用いて$||q||^{2}=C_1, \, ||\mathbf{x}_{i}||^{2}=C_2$のように表せるとき、$(1.3)$式は下記のように同値変形できる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{||q|| ||\mathbf{x}_{i}||} &= \mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{C_1 C_2} \\
&= \mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$

上記より、$\mathbf{x}_{i}$のノルムが同じ場合は「同一のクエリ$q$についてのK-MIPS問題がK-MCSS問題に帰着する」ことが確認できる。

クラスタリングを用いた最大内積探索の効率化

k-means

実際の問題でK-MIPS・K-NNS・K-MCSS問題をそれぞれクエリ$q$とベクトル集合$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}$の総当たりで解こうとすると計算量が大きい場合が多い。

総当たりで計算を行う場合は計算量が大きい一方で正確な結果が得られるが、「検索」のように概ね高い類似性が得られればよく「厳密な正確さ」が必要ない場合も多くある。このような際に、k-means法を用いたクラスタリングに基づく解の近似も有力な手法となる。

具体的には下記のような手順に基づいて近似解を得ることができる。
$[1] \,$ ベクトル集合$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}$をk-means法に基づいて$k$個のクラスタに分類
$[2] \,$ クエリ$q$とクラスタの平均ベクトルの内積 or 類似度を計算、値の大きなクラスタを選択
$[3] \,$ 類似度の高いクラスタからクエリ$q$との類似度が高いベクトル$\mathbf{x}_{i}$を選択

上記の$[1]$は参考論文では下記のようなアルゴリズムの形式で表される。

Algorithm$. 1 \,$ (Clustering is efficient for approximate maximum inner product search.)

上記のようにクラスタの平均ベクトルとの内積 or 類似度を計算することによって、計算量を減らすことが可能である。たとえば$10,000$ベクトルを$100$個のクラスタに$100$ずつ分類する場合、類似度の計算回数は$100 \times 2 = 200$であり、総当たりの$10,000$から大きく減らすことができる。

一方で、クエリ$q$がクラスタの境界付近に位置する場合など、必ずしも厳密な結果が得られるわけではないことに注意が必要である。この課題に対してはクラスタを複数選ぶなどの対応策が用いられる場合も多い。

階層k-means

前項で確認を行ったk-meansクラスタリングに基づく近似では「クラスタの数が多い：精度が高いが計算量が多い」、「クラスタの数が少ない：計算量が少ないが精度も低い」というトレードオフがある。この問題については階層k-meansが一つの解決策になりうる。

Figure$. 1 \,$ (Clustering is efficient for approximate maximum inner product search.)

上図のようにベクトルをいくつかの階層型のクラスタに分類しておくことで順々に分類を行うことが可能になる。たとえば$10,000$を$1,000$を$10$個、$1,000$を$10$個、$100$を$10$個のように階層的に分類すると、探索の計算量は$10 \times 4$まで削減できる。

この階層型クラスタは、多くのクラスタを先に作り、徐々に階層型クラスタリングを行うことで構築が可能である。

ウォリスの公式の導出とウォリスの公式を用いた円周率の近似計算

投稿日: 投稿者: lib-arts

ウォリスの公式は円周率の近似などにあたって役立つ公式で、ウォリス積分(Wallis integral)の式から導出を行うことができます。当記事ではウォリス積分に基づくウォリスの公式の導出とPythonを用いた円周率の近似計算例について取り扱いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$4$章「積分($1$変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(10/25 15:16時点)
Amazon

ウォリスの公式の導出

ウォリス積分の公式

ウォリス積分の公式は下記のように表される。
$$
\large
\begin{align}
\int_{0}^{\frac{\pi}{2}} \cos^{2m}{x} dx &= \int_{0}^{\frac{\pi}{2}} \sin^{2m}{x} dx = \frac{(2m-1)!!}{2m!!} \cdot \frac{\pi}{2} \quad (1) \\
\int_{0}^{\frac{\pi}{2}} \cos^{2m+1}{x} dx &= \int_{0}^{\frac{\pi}{2}} \sin^{2m+1}{x} dx = \frac{2m!!}{(2m+1)!!} \quad (2) \\
m & \in \mathbb{N}
\end{align}
$$

ウォリスの公式の導出

$\displaystyle x \in \left[ 0, \frac{\pi}{2} \right]$の$x$について、$0 \leq \sin{x} \leq 1$であるので下記が成立する。
$$
\large
\begin{align}
\sin^{2n+2}{x} \leq \sin^{2n+1}{x} \leq \sin^{2n}{x}
\end{align}
$$

上記は$\displaystyle x \in \left[ 0, \frac{\pi}{2} \right]$の任意の$x$について成立するので、下記が成立する。
$$
\large
\begin{align}
\int_{0}^{\frac{\pi}{2}} \sin^{2n+2}{x} dx \leq \int_{0}^{\frac{\pi}{2}} \sin^{2n+1}{x} dx \leq \int_{0}^{\frac{\pi}{2}} \sin^{2n}{x} dx
\end{align}
$$

上記に対し、ウォリス積分をそれぞれ適用することで下記が得られる。
$$
\large
\begin{align}
\int_{0}^{\frac{\pi}{2}} \sin^{2n+2}{x} dx \leq & \int_{0}^{\frac{\pi}{2}} \sin^{2n+1}{x} dx \leq \int_{0}^{\frac{\pi}{2}} \sin^{2n}{x} dx \\
\frac{(2n+1)!!}{(2n+2)!!} \cdot \frac{\pi}{2} \leq & \frac{(2n)!!}{(2n+1)!!} \leq \frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2} \\
\frac{2n+1}{2n+2} \cdot \frac{\pi}{2} \leq & \frac{(2n)!!}{(2n+1)!!} \cdot \frac{(2n)!!}{(2n-1)!!} \leq \frac{\pi}{2}
\end{align}
$$

ここで$\displaystyle \lim_{n \to \infty} \frac{2n+1}{2n+2} = 1$なので、下記が成立する。
$$
\large
\begin{align}
\lim_{n \to \infty} \frac{(2n)!!}{(2n+1)!!} \cdot \frac{(2n)!!}{(2n-1)!!} &= \frac{2^{2} \cdot 4^{2} \cdot 6^{2} \cdot \cdots}{(1 \cdot 3)(3 \cdot 5)(5 \cdot 7) \cdots} \\
&= \prod_{n=1}^{\infty} \frac{(2n)^{2}}{(2n-1)(2n+1)} \\
&= \frac{\pi}{2}
\end{align}
$$

円周率の近似

下記のような計算を行うことでウォリスの公式に基づいて円周率の近似を行うことができる。

import numpy as np

pi = 2.
for i in range(1000):
    n = i+1
    pi = pi * (2*n)**2 / ((2*n-1)*(2*n+1))
    if n%200 == 0:
        print("n: {}, estimated_pi: {:.3f}".format(n, pi))

・実行結果

n: 200, estimated_pi: 3.138
n: 400, estimated_pi: 3.140
n: 600, estimated_pi: 3.140
n: 800, estimated_pi: 3.141
n: 1000, estimated_pi: 3.141

【Transformer】Sparse Attentionの分類とそれぞれの研究例

投稿日: 投稿者: lib-arts

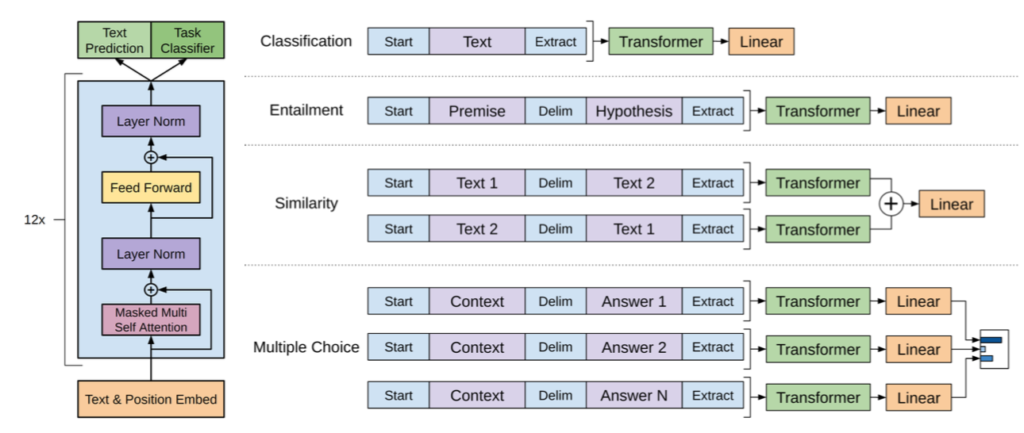
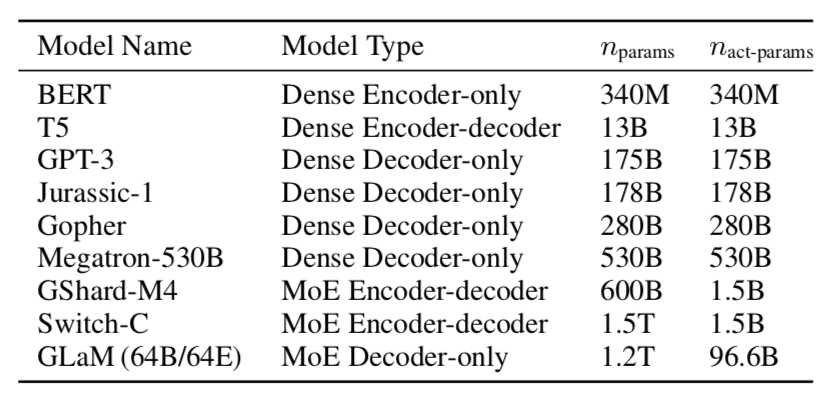
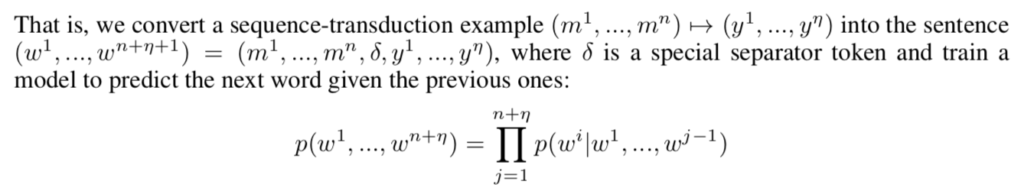Transformerの計算量は入力系列の長さの二乗に比例することから長い系列を取り扱う際に計算コストの課題が生じます。当記事ではこのような課題の解決にあたって用いられるSparse Attentionの分類とそれぞれの研究例について確認を行います。
作成にあたってはTransformerに関するSurvey論文である「A Survey of Transformers」やそれぞれの論文を参考にしました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

Sparse Attention

Sparse Attentionの概要

Transformerでは$Q K^{\mathrm{T}}$の計算に基づいてAttention Matrixの計算を行うが、このAttention Matrixの行列のサイズは系列の長さの二乗となり、計算コストが大きい。

このような際にAttention Matrixを疎行列で置き換える手法をSparse Attentionという。Aparse Attentionの活用にあたっては「どのような疎行列で表せば効率良く近似できるか」などを重視すると理解しやすい。

Sparse Attentionの分類

Sparse Attentionを実現する方法は「位置に基づく疎行列の作成」と「隠れ層のベクトルの類似度に基づく疎行列の作成」の二つに大別することができる。

当記事ではSurvey論文を元に位置に基づくSparse Attentionを「Position-based Sparse Attention」、隠れ層のベクトルの類似度に基づくSparse Attentionを「Content-based Sparse Attention」と表し、次節と次々節でそれぞれ取り扱う。

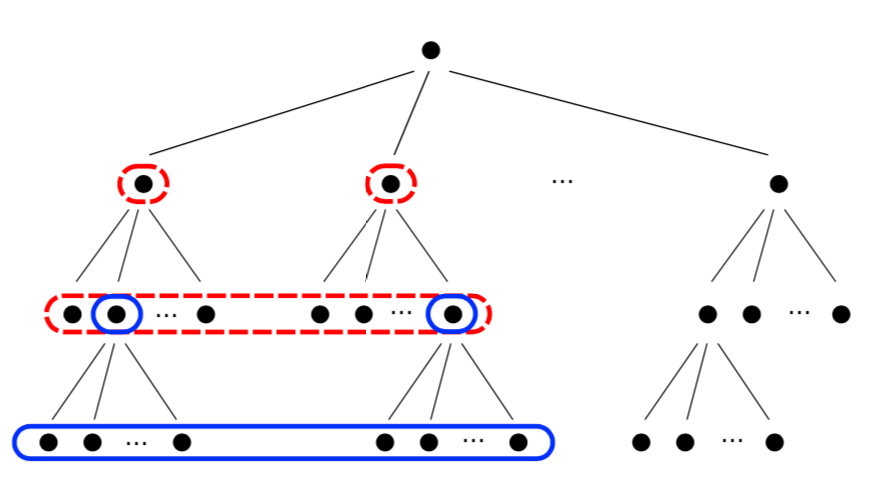
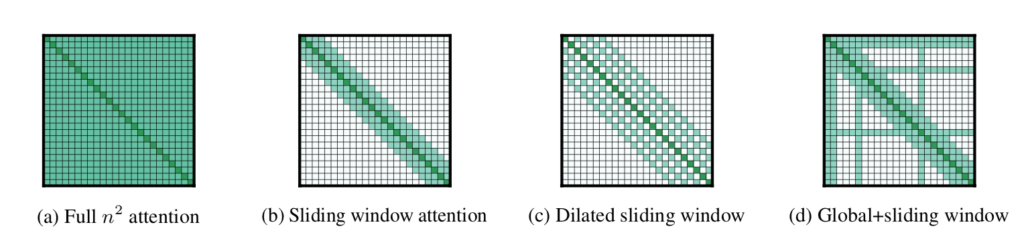
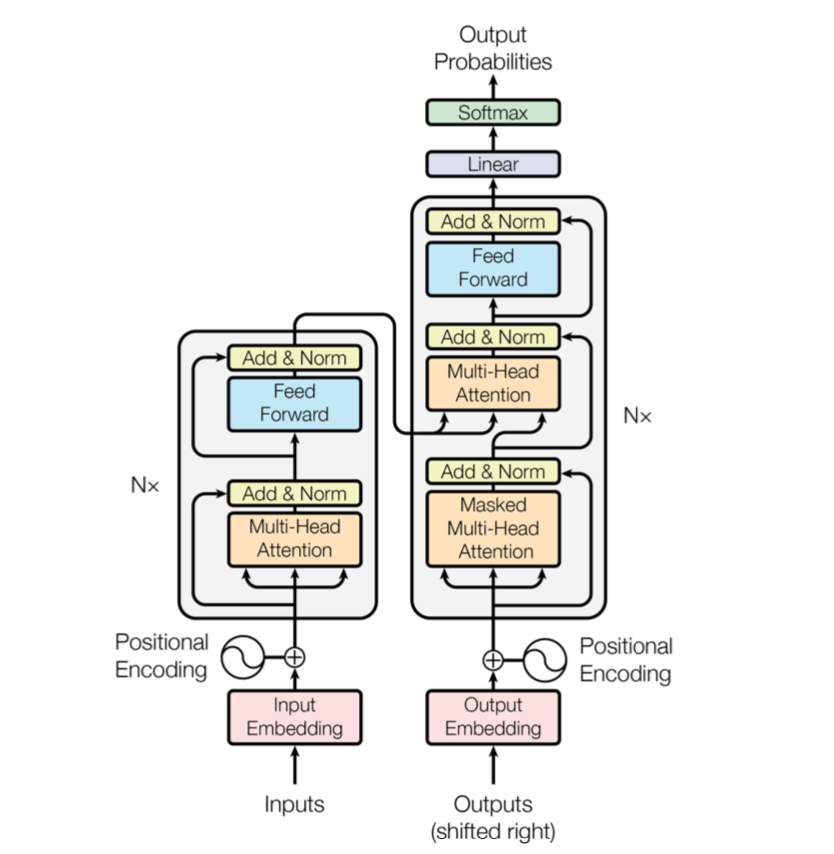
Position-based Sparse Attention

基本パターン

下図を元にPosition-based Sparse Attentionを構成する$5$つのパターンを確認することができる。

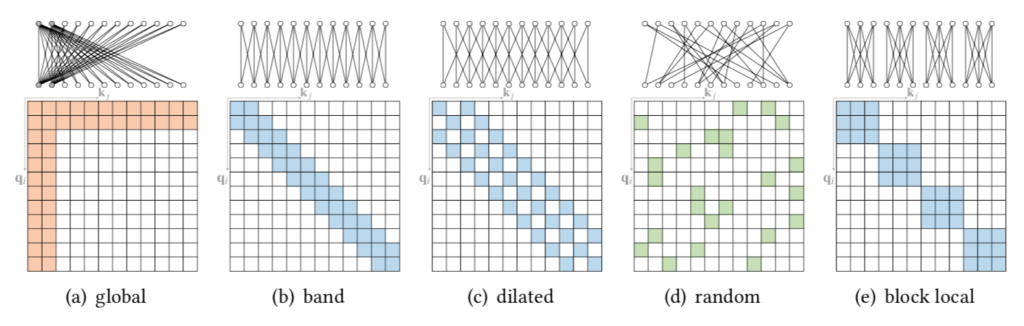
A Survey of TransformerのFig.$4$

図の上側が$l$層から$l+1$層を計算するにあたってのAttentionの重みが$0$かどうかを表し、下側がAttention Matrixの数値に対応する($0$の場合白、$0$以外の場合色付けされる)。上側が特殊な形式のグラフ、下側が隣接行列であると解釈することもできる。

以下で取り扱うStar-Transformer、Longformer、ETC、BigBirdなどの研究ではそれぞれこの基本パターンの組み合わせによってSparse Attentionを構成する。

基本パターンの解釈

基本パターンの解釈を以下にまとめた。

global特定のトークン(ノード)を全てのトークンのAttention計算に用いるかつ、特定のトークンのAttention計算には全てのトークンの隠れ層を用いる。
band近隣のトークンのみを用いてAttention計算を行う。CNNとRNNはbandの特殊な例であると解釈することもできる。
dilatedbandによる局所処理のreceptive field(特定の位置の出力を構成する入力領域)を広げるにあたって用いられる処理。詳しくはWaveNet論文などを参照すると良い。
randomランダムなグラフは完全グラフ(通常のTransformer)と似た性質を持つことを活用。
block local入力をセグメント単位に分けてAttention計算を行う。

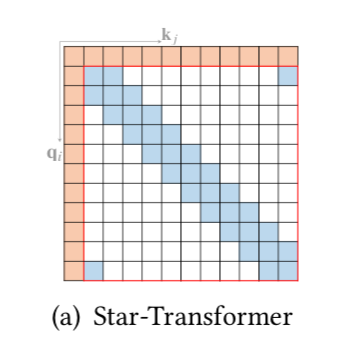
Star-Transformer

A Survey of TransformerではStar-Transformerが下記のような図で表される。

A Survey of Transformer：Fig.$5$.(a)

上図より、Star-Transformerが「global attention」と「band attention」の組み合わせであることが確認できる。

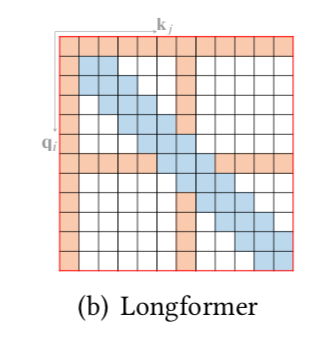
Longformer

A Survey of TransformerではLongformerが下記のような図で表される。

A Survey of Transformer：Fig.$5$.(b)

上図より、Star-Transformerが「global attention」と「band attention」の組み合わせであることが確認できる。

Longformer論文 Figure$\, 2$

また、上図で表されるLongformer論文のFigure$\, 2$より、Attention Matrixの詳細が確認できる。Surveyでは「global」＋「band」のみが記載されているが、Longformer論文では「global」＋「dilated」のパターンも記載されている。

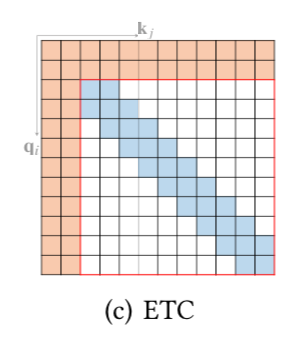
ETC

A Survey of TransformerではETC(Extended Transformer Construction)が下記のような図で表される。

A Survey of Transformer：Fig.$5$.(c)

上図より、ETCがStar-Transformerと同様に「global attention」と「band attention」の組み合わせであることが確認できる。

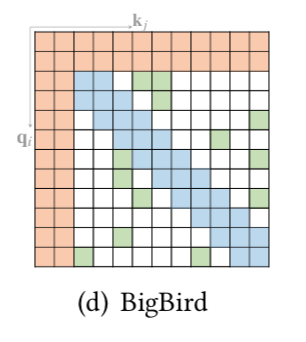
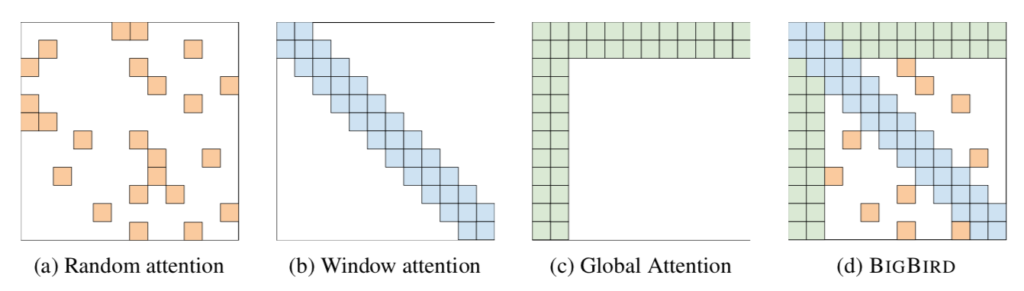
BigBird

A Survey of TransformerではBig Birdが下記のような図で表される。

A Survey of Transformer：Fig.$5$.(d)

上図より、Big Birdが「global attention」＋「band attention」＋「random attention」であることが確認できる。

Big Bird論文 Figure$\, 1$

また、Big Bird論文でもSurveyと同様な図が確認できる。色遣いが近いことから、Surveyの図はBig Birdをある程度参考に作成したことが推察される。

Content-based Sparse Attention

Content-based Sparse Attentionでは隠れ層のベクトルの値に基づいてAttention Matrixを疎行列で表す手法である。以下、LSH(locality-sensitive hashing)を用いるReformerやRouting Transformerなどの具体的な研究例について確認を行う。

Reformer

ReformerはLSH(locality-sensitive hashing)に基づくLSH AttentionというSparse Attentionを行う。以下、LSHとLSH Attentionについて確認を行う。

locality-sensitive hashing

次元$d_{k}$のベクトル$\mathbf{x} \in \mathbb{R}^{d_{k}}$を$b$値に分類するハッシュ関数を$h$とおく。このとき$h(\mathbf{x}) \in \{1, 2, \cdots, b \}$である。

Reformer論文では乱数に基づく行列$R \in \mathbb{R}^{d_{k} \times b/2}$に基づいてハッシュ関数$h$を定める。ハッシュ関数の定義にあたって、$[\mathbf{u}; \mathbf{v}]$をベクトル$\mathbf{u}$と$\mathbf{v}$の連結(concatnation)であると定義する。

このときハッシュ関数$h(\mathbf{x})$を下記のように定義する。
$$
\large
\begin{align}
h(\mathbf{x}) = \mathrm{argmax}([ \mathbf{x}R; -\mathbf{x}R])
\end{align}
$$

上記の$\mathbf{x}R$が要素数$\displaystyle \frac{b}{2}$のベクトルであるので、ハッシュ関数$h$は要素数$b$のベクトル$[\mathbf{x}R; -\mathbf{x}R]$から最大値を持つインデックスを選択する関数であると解釈できる。

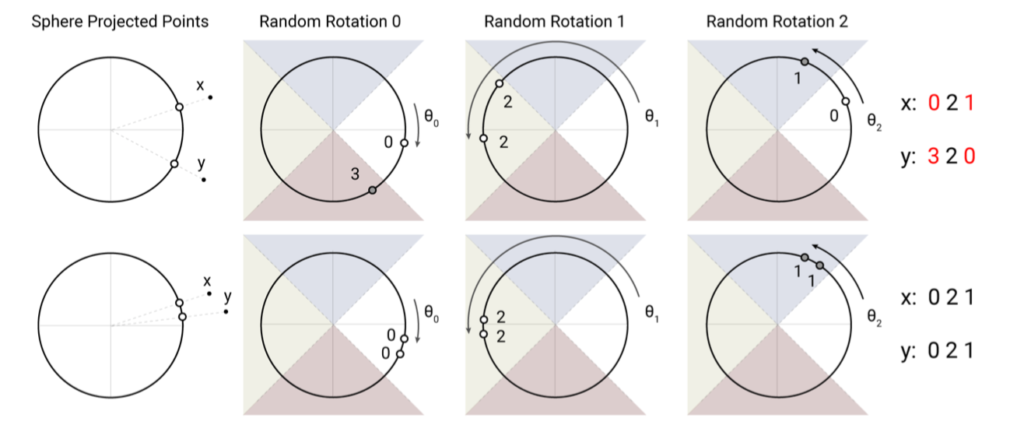
locality-sensitive hashingでは行列$R$がランダムにベクトルを回転させる行列であると解釈することもできるので、直感的には下図のような図を元に理解しておくとと良い。

Reformer論文 Figure$\, 1$

ReformerにおけるLSH Attentionは当項で確認を行なったハッシュ関数$h$に基づくlocality-sensitive hashingを用いたSparse Attentionである。

LSH Attention

LSH AttentionではTransformerのself-Attentionの式を下記のように改変を行う。
$$
\large
\begin{align}
o_{i} &= \sum_{j \in \mathcal{P}_{i}} \exp{\left( q_{i} \cdot k_{j} \; – \, z(i, \mathcal{P}_{i}) \right)} v_{j} \\
\mathcal{P}_{i} &= \{ j: i \geq j \}
\end{align}
$$

上記の理解にあたっては$\mathcal{P}_{i}$が「位置$i$のqueryである$q_{i}$が類似する位置の集合」であることに着目することが重要である。また、$z$は分配関数(partition function)であり、ソフトマックス関数と同様に出力の正規化を行う関数である。

LSH Attentionでは集合$\mathcal{P}_{i}$を前項で定義したハッシュ関数$h$を用いて下記のように定義する。
$$
\large
\begin{align}
\mathcal{P}_{i} = \{ j : h(q_{i}) = h(k_{j}) \}
\end{align}
$$

上記は「位置$i$に対して$h(q_{i}) = h(k_{j})$が成立する位置$j$の集合を$\mathcal{P}_{i}$と定義する」と解釈することができる。

Routing Transformer

Routing Transformerではクラスタリングと同様の枠組みを用いてSparse Attention処理を行う。以下、クラスタリングに基づくSparse Attentionの計算とクラスタリングに用いるCentroid vectorsの計算について確認する。

Routing Attention

Routing Transformer論文では下記のような式でSparse Attentionの計算を行う。
$$
\large
\begin{align}
X_{i}’ &= \sum_{\substack{j: \mu(K_{j}) = \mu(Q_{i}), \\ j<i}} A_{ij} V_j \\
\mu(Q_{i}) & \in \{ 1, 2, \cdots , k \}, \, \mu(K_{j}) \in \{ 1, 2, \cdots , k \} \\
\boldsymbol{\mu} &= (\mu_{1}, \cdots , \mu_{k}), \quad \mu_{l} \in \mathbb{R}^{d}
\end{align}
$$

上記の式はRouting Transformer論文の$(8)$式に改変を行なったものである。$A$はAttention Matrix、$i$は位置$i$のインデックス、$j$はAttention処理後の位置$i$の隠れ層を計算するにあたって用いる位置$j$のインデックスをそれぞれ表す。$j$は$A$の列に対応する一方で、$V$の行に対応することに注意が必要である。また、$X_{i}’$はFFN層の入力に用いるAttentionの処理結果、$\mu(Q_{i})$は$Q_i$に最も近いCentroid vectorのインデックスを得る関数である。

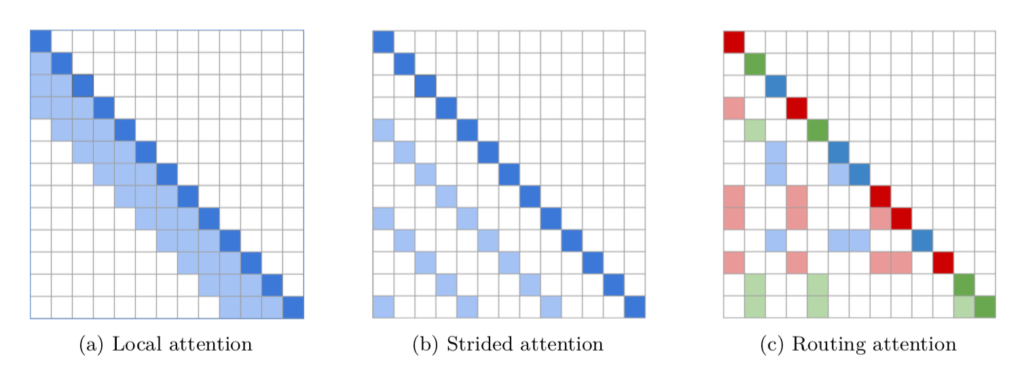
上記のSparse AttentionにおけるAttention Matrixは下図のように図示することができる。

Routing Transformer論文 Figure$\, 1$

$(a)$と$(b)$は前節で取り扱ったPosition-based Sparse Attentionの計算を自己回帰的(auto regressive)に表したものである。同様に$(c)$がRouting Transformerで用いるRouting Attentionに対応する。

$(c)$の理解にあたっては、まず図では「赤・青・緑」の三色に$3$つのクラスタを対応させたと解釈すると良い。ここで「緑」の行に注目すると、$(5,2)$成分が薄い緑で表されていることが確認できる。この$(5,2)$成分は同じクラスタの位置の隠れ層を参照することに対応する。同様に下からの$2$行は緑であるが、どちらも$2$列目と$5$列目が薄い緑で表されており、$2$番目と$5$番目の隠れ層を参照してそれぞれ計算を行うことも確認できる。

このようにRouting TransformerにおけるRouting Attentionではそれぞれの隠れ層を$k$個のクラスタに分類し、その分類結果に基づいてSparseなAttention Matrixの生成を行う。

Centroid vectorsの計算

前項で確認を行ったRouting Attentionはクラスタリングの結果に基づいてSparse Attentionの計算を行う手法である。当項ではクラスタリングに用いるCentroid vectorsの$\boldsymbol{\mu} = (\mu_{1}, \cdots , \mu_{k})$の計算について確認する。

$\boldsymbol{\mu} = (\mu_{1}, \cdots , \mu_{k})$はTransformerの隠れ層の次元である$d$次元の$k$個のベクトルに対応するので、下記のような行列で表すこともできる。
$$
\large
\begin{align}
\boldsymbol{\mu} \in \mathbb{R}^{k \times d}
\end{align}
$$

上記の$\boldsymbol{\mu}$は下記のような式に基づいて都度計算を行う。
$$
\large
\begin{align}
\mu_{l} \longleftarrow \lambda \mu_{l} + \frac{1-\lambda}{2} \sum_{i: \mu(Q_i) = l} Q_{i} + \frac{1-\lambda}{2} \sum_{j: \mu(Q_j) = l} K_{j}
\end{align}
$$

要確認：上記の計算では$\displaystyle \sum_{i: \mu(Q_i) = l} Q_{i}$のように和を計算する一方で、本来は平均を計算すべきではないか。

まとめ

参考

・Transformer論文：Attention is All you need[2017]
・A Survey of Transformer
・Star-Transformer
・Longformer
・ETC: Extended Transformer Construction
・Big Bird
・Reformer
・Routing Transformer

Transformerの構成の分類：Encoder-Decoder・Decoder onlyなど

投稿日: 投稿者: lib-arts

BERT・GPT-$3$などのTransformerの応用研究を理解するにあたってはEncoder-Decoder、Encoder only、Decoder onlyのようなTransformerの構成の分類を理解しておくと良いです。当記事ではそれぞれの概要や具体的な研究の分類を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

前提の確認

Transformerの仕組み

Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。

・直感的に理解するTransformer(統計の森作成)

Transformerの事前学習

Transformerは強力なモジュールである一方で、大量の学習セットが必要です。そこで予めWikipediaのような巨大なコーパスを元に事前学習(Pre-training)を行なったのちに手元のタスクについてfine-tuningを行うという形式で学習が行われることが多いです。

具体的にはBERT・T$5$・GPT-$3$などの研究が有名です。これらはLLM(Large Language Model)のように総称されることも多く、Transformerの事前学習は昨今の主要なトレンドであると解釈することもできます。

Transformerの構成の分類

概要

Transformerの構成はEncoder-Decoder、Encoder only、Decoder onlyに大別されます。

Transformer論文 Figure$\, 1$

Encoder-Decoder、Encoder only、Decoder onlyはどれもTransformer論文のFigure$\, 1$を元に理解することが可能です。以下、当節ではEncoder-Decoder、Encoder only、Decoder onlyについてそれぞれ詳しく確認を行います。

Encoder-Decoder

「Encoder-Decoder」はオリジナルのTransformerの論文で用いられた形式で、主に系列変換に用いられる構成です。

Transformer論文 Figure$\, 1$

上図の全体に対応しており、Encoderについて処理したのちにDecoderの処理を行います。このようなEncoder-Decoderの形式はRNNを用いた$2014$年のSequence to sequenceの研究と同様であり、この頃よく取り組まれていたタスクが機械翻訳であることにこの形式は起因すると解釈できます。

Transformerがこの機械翻訳タスクで高いパフォーマンスを示したことで、その後様々な応用研究がなされるようになり、用いられるTransformerの形式も多様化しました。T$5$もEncoder-Decoderの形式であることも合わせて抑えておくと良いと思います。

Encoder only

オリジナルのTransformerがEncoder-Decoderの形式である一方で、Transformerの応用研究で有名なBERTではFine-tuningによって分類タスクを中心に取り扱うことからEncoder onlyの形式が用いられます。

Decoder only

Decoderのみを用いるTransformerはBERTのようなEncoder onlyと反対にDecoderのみを用いて学習を行います。

Transformer Decoder論文の本文

Transformer Decoder論文では上記のような数式に基づいて誤差関数の定義や学習を行いますが、同様のlossはGPT系列でも用いられることからChatGPTやGPT-$4$も概ね同じような構成であることが推測できます。

GPT論文のFigure$\, 1$

上図はGPT論文のFigure$\, 1$で、図の左側がTransformerの論文の図のDecoderに一致することが確認できます。

Decoder onlyを理解するにあたって重要になるのがMasked Attention(Transformerの論文の図ではMasked Multi Head Attention、GPT論文の図ではMasked Multi Self Attention)です。

Masked Attention: Transformerの論文より
Masked Attention: Transformer Decoderの論文より

上記はTransformer論文とTransformer Decoder論文のMasked Attentionについての記載です。時系列が逆にならないようにAttentionを計算する際の行列(隣接行列)をマスクすると解釈して良いと思います。

より具体的には対角成分より上の成分が$0$かつそれ以外の成分が$1$である下三角行列を用いてAttentionに用いる行列との要素積を計算すれば自己回帰(Auto Regressive)処理を実現することができます。

具体的な研究の分類

具体的な研究の分類はGLaM(Generalist Language Model)論文のTable$\, 2$が参考になります。

GLaM論文 Table$\, 2$

GPT-$3$以外にもGopherやGLaMでDecoder onlyが用いられることから、LLMの研究ではDecoder onlyが用いられることが多いと解釈して良いと思います。

自動微分の理論と応用⑤：TransformerとDot Product Attention

投稿日: 投稿者: lib-arts

自動微分(Automatic Differentiation)は大規模なニューラルネットワークであるDeepLearningの学習における誤差逆伝播などに用いられる手法です。当記事ではDot Product Attentionに基づくTransformerの簡易版の実装を行いました。
作成にあたっては「ゼロから作るDeep Learning②」の第$5$章「リカレントニューラルネットワーク」の内容を主に参照しました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

ゼロから作るDeep Learning ❷ ―自然言語処理編

ゼロから作るDeep Learning ❷ ―自然言語処理編

斎藤 康毅
3,960円(10/26 03:20時点)
Amazon

・直感的に理解するTransformerの仕組み

Dot Product Attention

ソフトマックス関数

def softmax(a):    # a is 2D-Array
    c = np.max(a, axis=1)
    exp_a = np.exp(a.T-c)
    sum_exp_a = np.sum(exp_a, axis=0)
    y = (exp_a / sum_exp_a).T
    return y

def softmax_3D(a):    # a is 3D-Array
    N, L, H = a.shape
    c = np.max(a, axis=2)
    exp_a = np.exp(a-c.reshape([N, L, 1]).repeat(H, axis=2))
    sum_exp_a = np.sum(exp_a, axis=2)
    y = exp_a / sum_exp_a.reshape([N, L, 1]).repeat(H, axis=2)
    return y

class Softmax:
    def __init__(self):
        self.loss = None
        self.y = None

    def forward(self, x):
        self.y = softmax_3D(x)
        return self.y

    def backward(self, dout):
        dx = dout * self.y * (1-self.y)
        return dx

内積の計算

Transformerの論文ではDot Product Attentionの計算を下記のように定義する。
$$
\large
\begin{align}
\mathrm{Attention}(K, Q, V) = \mathrm{softmax} \left( \frac{Q K^{\mathrm{T}}}{d_k} \right) V
\end{align}
$$

上記の$\displaystyle \mathrm{softmax} \left( \frac{Q K^{\mathrm{T}}}{d_k} \right)$の演算は下記のように実装することができる。

class CalcAttentionWeight:
    def __init__(self):
        self.h = None
        self.graph = None
        self.softmax = Softmax()

    def forward(self, h):
        self.h = h
        N, L, H = self.h.shape
        scaled_dp = np.zeros([N, L, L])
        for i in range(N):
            scaled_dp[i, :, :] = np.dot(h[i, :, :], h[i, :, :].T) / np.sqrt(H)

        self.graph = self.softmax.forward(scaled_dp)

        return self.graph

    def backward(self, dgraph):
        N, L, H = self.h.shape
        ds = self.softmax.backward(dgraph)
        dh = np.zeros_like(self.h)
        for i in range(N):
            dh[i, :, :] = 2*np.dot(dgraph[i, :, :], self.h[i, :, :]) / np.sqrt(H)
        return dh

上記のbackwardメソッドの計算にあたっては、行列$X$について下記のような行列微分が成立することを用いた。
$$
\large
\begin{align}
\frac{\partial}{\partial X} (X X^{\mathrm{T}}) = 2 X = \frac{\partial}{\partial X} (X^{\mathrm{T}} X)
\end{align}
$$

TransformerのDot Product Attentionでは行列の$Q$と$K$にどちらも隠れ層を用いるので、上記の計算が基本的に対応する。

Dot Product Attention

class MessagePassing3D:
    def __init__(self, adj_mat_3D):
        self.params, self.grads = [], []
        self.graph = adj_mat_3D
        self.h = None

    def forward(self, h):
        self.h = h
        N, L, H = h.shape
        m_t = np.zeros_like(h)
        for i in range(self.graph.shape[1]):
            ar = self.graph[:, i,:].reshape(N, L, 1).repeat(H, axis=2)
            t = h * ar
            m_t[:, i, :] = np.sum(t, axis=1)
        return m_t

    def backward(self, dm_t):
        N, L, H = self.h.shape
        dh = np.zeros_like(self.h)
        dar = np.zeros_like(self.graph)
        for i in range(self.graph.shape[1]):
            ar = self.graph[:, i, :].reshape(N, L, 1).repeat(H, axis=2)
            dh[:, i, :] = np.sum(dm_t * ar, axis=1)
        for i in range(self.graph.shape[0]):
            dar[i, :, :] = np.dot(dm_t[i, :, :], self.h[i, :, :].T)
        return dh, dar

基本的にはグラフニューラルネットワークと同様の実装を行なったが、内積による類似度計算を反映できるようにグラフの隣接行列に対応する配列を(L,L)から(N,L,L)に変えた。

自動微分・誤差逆伝播の理論と応用④：Attentionとグラフニューラルネットワーク

Transformer

Transformerレイヤーの計算

Affineクラス

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        return dx

Affineクラスについては下記で詳しく取り扱った。

自動微分・誤差逆伝播の理論と応用②：Affine変換の自動微分とニューラルネットワークの実装

Transformer_Layerクラス

class Transformer_Layer:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.dW = np.zeros_like(W)
        self.db = np.zeros_like(b)
        self.h = None
        self.affines = []
        self.graph = None
        self.calc_mp = None
        self.calc_weight = CalcAttentionWeight()

    def forward(self, h):
        self.h = h
        self.graph = self.calc_weight.forward(self.h)
        self.calc_mp = MessagePassing3D(self.graph)
        m_t = self.calc_mp.forward(h)
        h_next = np.zeros_like(h)
        for i in range(self.graph.shape[1]):
            affine = Affine(self.W, self.b)
            h_next[:, i, :] = affine.forward(m_t[:, i, :])
            self.affines.append(affine)
            
        return h_next

    def backward(self, dh_next):
        N, T, H = self.h.shape
        
        dh_affine = np.zeros_like(self.h)
        for i in range(self.graph.shape[1]):
            dh_affine[:, i, :] = self.affines[i].backward(dh_next[:, i, :])
            self.dW += self.affines[i].dW
            self.db += self.affines[i].db
            
        dh_mp, dgraph = self.calc_mp.backward(dh_affine)
        dh = self.calc_weight.backward(dgraph)
        return dh_mp+dh

$2$層Transformer

出力層

class Aggregate:
    def __init__(self):
        self.h = None
        self.y = None

    def forward(self, h):
        self.h = h
        self.y = np.sum(h, axis=1)
        return self.y

    def backward(self, dy):
        N, T, H = self.h.shape
        dh = dy.reshape(N, 1, H).repeat(T, axis=1)
        return dh

def cross_entropy_error(y,t):
    delta = 1e-7
    return -np.sum(t * np.log(y+delta))

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss

    def backward(self, dout=1.):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        return dx

$2$層Transformer

from collections import OrderedDict

class TwoLayerTransformer:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        self.params = {}
        self.params["W1"] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params["b1"] = np.zeros(hidden_size)
        self.params["W2"] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params["b2"] = np.zeros(output_size)

        # generate layers
        self.layers = OrderedDict()
        self.layers["Transformer_layer1"] = Transformer_Layer(self.params["W1"], self.params["b1"])
        self.layers["Softmax1"] = Softmax()
        self.layers["Transformer_layer2"] = Transformer_Layer(self.params["W2"], self.params["b2"])
        self.layers["Aggregate"] = Aggregate()
        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        return x

    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

    def calc_gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = self.lastLayer.backward(1.)
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # output
        grads = {}
        grads["W1"] = self.layers["Transformer_layer1"].dW
        grads["b1"] = self.layers["Transformer_layer1"].db
        grads["W2"] = self.layers["Transformer_layer2"].dW
        grads["b2"] = self.layers["Transformer_layer2"].db

        return grads

実行例

np.random.seed(0)

alpha = 0.1

x = np.ones([2, 5, 2])
x[0, :, :1] = -1.
t = np.array([[1., 0.], [0., 1.]])

network = TwoLayerTransformer(2, 2, 2)

for i in range(50):
    grad = network.calc_gradient(x, t)

    for key in ("W1", "b1", "W2", "b2"):
        network.params[key] -= alpha * grad[key]

    if (i+1)%10==0:
        print(softmax(network.predict(x)))

・実行結果

[[0.46977806 0.53022194]
 [0.46352429 0.53647571]]
[[0.73811463 0.26188537]
 [0.30103311 0.69896689]]
[[0.96535871 0.03464129]
 [0.03273874 0.96726126]]
[[0.99548783 0.00451217]
 [0.00521023 0.99478977]]
[[9.99530595e-01 4.69404946e-04]
 [1.19280865e-03 9.98807191e-01]]