下記などで取り扱った、乱数の生成に関する問題演習を通した理解ができるように問題・解答・解説をそれぞれ作成しました。

・標準演習$100$選
https://www.hello-statisticians.com/practice_100

基本問題

線形合同法・乗算型合同法

・問題
線形合同法(linear congruential method)は$1948$年頃にレーマー(Lehmer)が提案した手法で、仕組みがシンプルであるので乱数生成のイメージを掴むにあたって適した手法である。また、乗算型合同法は線形合同法の特殊な場合と考えられるので、両者は同時に理解することができる。
さて、線形合同法を理解するにあたっては、「整数に関する合同」と「数列の漸化式」の理解があれば十分であると思われる。以下の問題に答えよ。
i) $x_{n+1} = x_{n} + 2, x_1 = 1$のように表せるとき、$x_2, x_3$を求めよ。
ⅱ) $x_{n+1} = 2x_{n} + 1, x_1 = 1$のように表せるとき、$x_2, x_3$を求めよ。
ⅲ) 合同は「整数$x$を整数$M$で割った時の余りが等しいか」を表す概念である。このときの$M$を法(modulus)という。たとえば$2$と$5$は$3$で割った際にどちらも余りが$2$であるので、$3$を法とするとき合同であるといえる。このことは「$2 = 3 \quad (\mathrm{mod} \, 3)$」のように表すことができる。
上記に基づいて、法を$5$とするときに$2$と合同な自然数を$5$つ答えよ。
iv) $9$を法とするとき、$x_{n+1}=4x_{n}+2 \quad (\mathrm{mod} \, 9), x_1=1$に従って$x_2, x_3$を求めよ。
v) iv)の例の$x_4$以降を計算すると下記のようになる。
$$
\begin{align}
x_4=7, x_5=3, x_6=5, x_7=4, x_8=0, x_9=2, x_{10}=1, x_{11}=6, x_{12}=8
\end{align}
$$
上記には周期があると考えることができるが、どのような周期か答えよ。

・解答
i)
$x_2, x_3$は下記のように求めることができる。
$$
\begin{align}
x_2 &= x_{1} + 2 \\
&= 1 + 2 \\
&= 3 \\
x_3 &= x_{2} + 2 \\
&= 3 + 2 \\
&= 5
\end{align}
$$

ⅱ)
$x_2, x_3$は下記のように求めることができる。
$$
\begin{align}
x_2 &= 2x_{1} + 1 \\
&= 2 + 1 \\
&= 3 \\
x_3 &= 2x_{2} + 1 \\
&= 6 + 1 \\
&= 7
\end{align}
$$

ⅲ)
$$
\begin{align}
7, 12, 17, 22, 27
\end{align}
$$

iv)
$$
\begin{align}
x_2 &= 4x_{1} + 2 \\
&= 4 + 2 \\
&= 6 \\
x_3 &= 4x_{2} + 2 \\
&= 24 + 2 \\
&= 26 \\
&= 8 \quad (\mathrm{mod} \, 9)
\end{align}
$$

v)
$x_1$〜$x_9$と$x_{10}$〜$x_{18}$は一致し、これを周期とみなすことができる。線形合同法の計算の仕組み上、$1$度でも同じ値が出てくると以後の値は周期的に繰り返す。

・解説
線形合同法は「整数の合同」と「数列の漸化式」について理解していればそれほど難しくない手法だと思います。乗算合同法は線形合同法の定数項がないパターンであり、重複した値が得られやすい一方で計算コスト自体は低いため、合わせて抑えておくと良いと思います。
線形合同法、乗算型合同法の数式は下記でまとめたので、詳しくは下記も参照してみてください。
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html

具体的な分布への逆関数法の適用

・問題
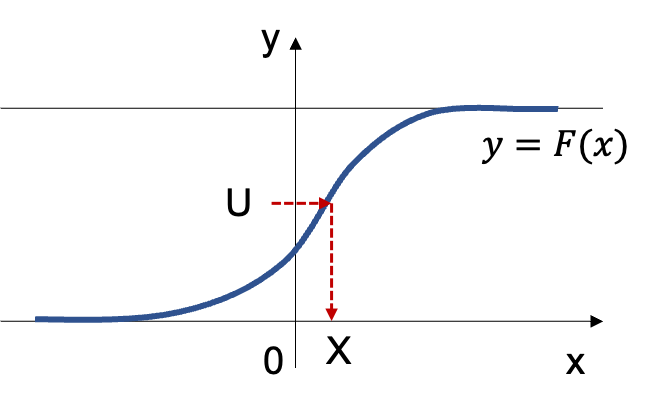
逆関数法は一様分布$\mathrm{Uniform}(0,1)$に基づく乱数を累積分布関数を持つ任意の確率分布と対応させることで確率分布に基づく乱数を生成させる手法である。逆関数の表記はやや分かりにくいので、下図に基づいて理解し立式や考察などを行うと良い。

以下、逆関数法の具体的な分布への適用を確認するにあたって、「指数分布」、「ロジスティック分布」、「コーシー分布」に関してそれぞれ確認を行う。ここまでの内容を元に下記の問いにそれぞれ答えよ。

i) $\lambda>0$のとき、指数分布$\mathrm{Ex}(\lambda)$の確率密度関数$f_1(x)$と累積分布関数$F_1(x)$を表せ。

ⅱ) $U \sim \mathrm{Uniform}(0,1)$に基づいて乱数$U$が得られるとき、i)で表した指数分布の累積分布関数$F_1(x)$を用いて$X_1 \sim \mathrm{Ex}(\lambda)$となる乱数$X_1$を一様乱数$U$を用いて表せ。

ⅲ) ロジスティック回帰などに用いられるロジスティック分布の累積分布関数は$\displaystyle F_2(x) = \frac{1}{1+e^{-x}}$のように表すことができる。ⅱ)と同様にロジスティック分布に基づく乱数$X_2$を一様乱数$U$を用いて表せ。

iv) コーシー分布の確率密度関数と累積分布関数をそれぞれ$f_3(x), F_3(x)$とおくと、下記のように表せる。
$$
\large
\begin{align}
f_3(x) &= \frac{1}{\pi (1+x^2)} \\
F_3(x) &= \int_{-\infty}^{x} f_3(u) du \\
&= \int_{-\infty}^{x} \frac{1}{\pi (1+u^2)} du
\end{align}
$$

$u=\tan{\theta}$を用いて変数変換を行うことで累積分布関数$F_3(x)$に関して下記が成立することを示せ。
$$
\large
\begin{align}
F_3(x) = \frac{1}{2} + \frac{1}{\pi} \tan^{-1}{x}
\end{align}
$$

v) ⅱ)と同様にコーシー分布に基づく乱数$X_3$を一様乱数$U$を用いて表せ。

・解答
i)
指数分布$\mathrm{Ex}(\lambda)$の確率密度関数$f_1(x)$と累積分布関数$F_1(x)$は下記のように表せる。
$$
\large
\begin{align}
f_1(x) &= \lambda e^{-\lambda x}, \quad x \geq 0 \\
F_1(x) &= 1 – e^{-\lambda x}, \quad x \geq 0
\end{align}
$$

ⅱ)
乱数$X_1$に関して下記が成立する。
$$
\large
\begin{align}
U &= 1 – e^{-\lambda X_1} \\
e^{-\lambda X_1} &= 1-U \\
-\lambda X_1 &= \log{(1-U)} \\
X_1 &= – \frac{1}{\lambda} \log{(1-U)} \\
& \rightsquigarrow – \frac{1}{\lambda} \log{U}
\end{align}
$$

上記の記号の$\rightsquigarrow$は$1-U$と$U$のどちらで表しても意味合いが変わらないことを表すにあたって用いた。一般的な用法ではないので用いることの少ない記号を選定した。

ⅲ)
乱数$X_2$に関して下記が成立する。
$$
\large
\begin{align}
U &= \frac{1}{1+e^{-X_2}} \\
1+e^{-X_2} &= \frac{1}{U} \\
e^{-X_2} &= \frac{1-U}{U} \\
-X_2 &= \log{\frac{1-U}{U}} \\
X_2 &= -\log{\frac{1-U}{U}} \\
&= \log{\frac{U}{1-U}}
\end{align}
$$

iv)
$u=\tan{\theta}$を用いて変数変換を行うことで累積分布関数$F_3(x)$は下記のように変形できる。
$$
\large
\begin{align}
F_3(x) &= \int_{-\infty}^{x} \frac{1}{\pi (1+u^2)} du \\
&= \frac{1}{2} + \int_{0}^{x} \frac{1}{\pi (1+u^2)} du \\
&= \frac{1}{2} + \int_{0}^{\tan^{-1}{x}} \frac{1}{\pi (1+\tan{\theta})} \cdot \frac{1}{\cos^{2}{\theta}} d \theta \\
&= \frac{1}{2} + \int_{0}^{\tan^{-1}{x}} \frac{\cancel{\cos^{2}{\theta}}}{\pi \cancel{\cos^{2}{\theta}}} d \theta \\
&= \frac{1}{2} + \left[ \frac{1}{\pi} \theta \right]_{0}^{\tan^{-1}{x}} \\
&= \frac{1}{2} + \frac{1}{\pi} \tan^{-1}{x}
\end{align}
$$

v)
乱数$X_3$に関して下記が成立する。
$$
\large
\begin{align}
U &= \frac{1}{2} + \frac{1}{\pi} \tan^{-1}{X_3} \\
\tan^{-1}{X_3} &= \pi \left( U – \frac{1}{2} \right) \\
X_3 &= \tan{ \left[ \left( U – \frac{1}{2} \right) \pi \right] }
\end{align}
$$

・解説
下記などを元に作成を行いました。

M系列とビット演算

・問題
「線形合同法・乗算型合同法」は多次元の一様分布の生成を行う際に適切な乱数が得られない「多次元疎結晶構造」を生じる。よって、実用的にはM系列という考え方に基づく一様乱数が用いられることが多く、現在多く使われるメルセンヌ・ツイスタ法もM系列に基づいた手法である。

この問題では以下、M系列に基づく乱数生成の手法について演習形式で確認を行う。下記の問いにそれぞれ答えよ。
i) M系列では$2$で割った余りに基づく$\mathrm{mod} \, 2$を元に乱数の生成を行う。$3=1 \, (\mathrm{mod} \, 2)$のような表記に基づいて、$2,5,8$を表せ。

ⅱ) 線形合同法や乗算型合同法では$x_n$に基づいて$x_{n+1}$の生成を行ったが、M系列では下記のような漸化式を用いる
$$
\begin{align}
x_{n+p} &= x_{n+q} + x_{n} \, (\mathrm{mod} \, 2) \quad \cdots \, (1) \\
p & > q
\end{align}
$$

$p=5, q=2$、$x_0=1, x_1=1, x_2=0, x_3=0, x_4=1$のとき、$x_5, x_6, x_7, x_8, x_9$をそれぞれ計算せよ。

ⅲ) $x_{n+q} \in \{ 0,1 \} , x_{n} \in \{ 0,1 \}$のとき、排他的論理和の$\oplus$を用いて$(1)$式は下記のように表せる。
$$
\begin{align}
x_{n+p} &= x_{n+q} \oplus x_{n} \\
p & > q
\end{align}
$$

$\oplus$の定義に基づいて$0 \oplus 0, 1 \oplus 0, 1 \oplus 1$をそれぞれ計算せよ。

iv) ⅱ)で得られた$x_0$〜$x_9$を$2$つずつ$X_0=11_{(2)}, X_1=00_{(2)}, X_2=11_{(2)}, X_3=11_{(2)}, X_4=10_{(2)}$で表す。ここで$(2)$は$2$進数表記であることを表すにあたって用いた。$X_0$〜$X_4$をそれぞれ$10$進数表記で表せ。

v) $X_n$に関して下記のような演算を定める。
$$
\begin{align}
X_{n+5} &= X_{n+2} \oplus X_{n}
\end{align}
$$

上記の$\oplus$は桁毎に排他的論理和を定義したと考えるとき、プログラムなどを元に$X_{100}$まで生成し、$0$〜$3$が概ね均等に得られることを確認せよ。

・解答
i)
$2,5,8$は$\mathrm{mod} \, 2$に基づいて下記のように表すことができる。
$$
\begin{align}
2 &= 0 \, (\mathrm{mod} \, 2) \\
5 &= 1 \, (\mathrm{mod} \, 2) \\
8 &= 0 \, (\mathrm{mod} \, 2)
\end{align}
$$

ⅱ)
$x_5, x_6, x_7, x_8, x_9$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
x_5 &= x_2 + x_0 = 0 + 1 = 1 \, (\mathrm{mod} \, 2) \\
x_6 &= x_3 + x_1 = 0 + 1 = 1 \, (\mathrm{mod} \, 2) \\
x_7 &= x_4 + x_2 = 1 + 0 = 1 \, (\mathrm{mod} \, 2) \\
x_8 &= x_5 + x_3 = 1 + 0 = 1 \, (\mathrm{mod} \, 2) \\
x_9 &= x_6 + x_4 = 1 + 1 = 0 \, (\mathrm{mod} \, 2)
\end{align}
$$

ⅲ)
$\oplus$の定義に基づいて$0 \oplus 0, 1 \oplus 0, 1 \oplus 1$は下記のように計算できる。
$$
\large
\begin{align}
0 \oplus 0 &= 0 \\
1 \oplus 0 &= 1 \\
1 \oplus 1 &= 0
\end{align}
$$

iv)
$X_0$〜$X_4$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
X_0 &= 11_{(2)} = 1 \cdot 2^{1} + 1 \cdot 2^{0} = 3 \\
X_1=00_{(2)} = 0 \cdot 2^{1} + 0 \cdot 2^{0} = 0 \\
X_2=11_{(2)} = 1 \cdot 2^{1} + 1 \cdot 2^{0} = 3 \\
X_3=11_{(2)} = 1 \cdot 2^{1} + 1 \cdot 2^{0} = 3 \\
X_4=10_{(2)} = 1 \cdot 2^{1} + 0 \cdot 2^{0} = 2
\end{align}
$$

v)
下記を実行することで確認できる。

import numpy as np
import matplotlib.pyplot as plt

p, q = 5, 2

X = np.zeros(100+1)
X[:5] = np.array([3., 0., 3., 3., 2.])

for i in range(X.shape[0]-5):
    X[i+p] = int(X[i+q]) ^ int(X[i])

plt.hist(X)
plt.show()

実行結果

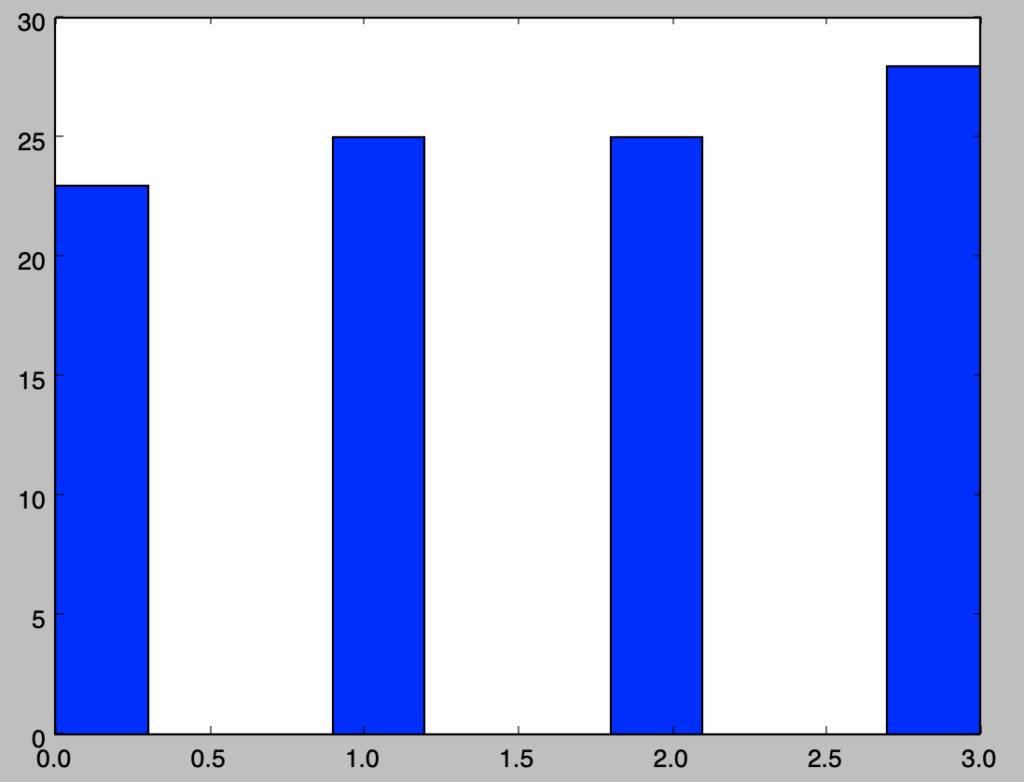
・解説
M系列は当問題で取り扱ったように$\mathrm{mod} \, 2$に基づいてビット演算を行うことで乱数の生成を行う手法です。M系列の詳細や近年よく用いられるメルセンヌ・ツイスタ法に関しては下記で詳しく取りまとめを行いました。

発展問題

モンテカルロ積分

・問題
モンテカルロ積分は乱数を用いて定積分の値を推定する手法であり、乱数を用いて数値計算を行う手法のモンテカルロ法の一種である。以下の問いにそれぞれ答えよ。

i) 関数$g(x)$に関する定積分$\displaystyle \theta = \int_{0}^{1} g(x) dx$の推定を行うことを考える。$X \sim \mathrm{Uniform}(0,1)$のとき$E[X]=1/2, E[g(X)]=\theta$であることを示せ。

ⅱ) i)より定積分$\displaystyle \theta = \int_{0}^{1} g(x) dx$の推定にあたっては$E[g(X)]$の推定を行えばよいと考えられる。$X \sim \mathrm{Uniform}(0,1)$に基づいて標本$x_1, x_2, \cdots x_n$が得られるとき標本を用いて$E[X]$の推定値を表せ。

ⅲ) ⅱ)の結果は大数の弱法則を考えることで$E[X]$に収束する。同様に考えることで$\theta=E[g(X)]$の推定量$\hat{\theta}$を$X_i \sim \mathrm{Uniform}(0,1)$を用いて表せ。

iv) ⅲ)の式に基づいてPythonなどのプログラムを用いて関数$g(x)=e^{-x}$について$\hat{\theta}$の推定値を計算を行い、$1-e^{-1}$に近い値が得られることを確認せよ。

v) $\displaystyle I = \int_{2}^{5} g(x) dx$の推定手順を示し、iv)と同様にプログラムなどを用いて推定値を計算せよ。

・解答
i)
一様分布$\mathrm{Uniform}(0,1)$の確率密度関数を$f(x)$とおくと、$E[X]$は下記のように表せる。
$$
\large
\begin{align}
E[X] &= \int_{0}^{1} x \cdot 1 dx \\
&= \left[ \frac{1}{2}x^2 \right]_{0}^{1} \\
&= \frac{1}{2}
\end{align}
$$

同様に$E[g(X)]$は下記のように表せる。
$$
\large
\begin{align}
E[g(X)] &= \int_{0}^{1} g(x) \cdot 1 dx \\
&= \int_{0}^{1} g(x) dx = \theta
\end{align}
$$

ⅱ)
$E[X]$の推定値は下記のように標本平均によって表される。
$$
\large
\begin{align}
\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align}
$$

ⅲ)
$\hat{\theta}$は下記のように表せる。
$$
\large
\begin{align}
\hat{\theta} = \frac{1}{n} \sum_{i=1}^{n} g(X_i)
\end{align}
$$

iv)

import numpy as np

np.random.seed(0)

X = np.random.rand(10000)
g_X = np.e**(-X)
g_x = 1-np.e**(-1)

print("Estimated E[g(X)]: {:.3f}".format(np.mean(g_X)))
print("E[g(X)]: {:.3f}".format(np.mean(g_x)))

実行結果

Estimated E[g(X)]: 0.634
E[g(X)]: 0.632

上記より類似の結果が得られたことが確認できる。

v)
一様分布$\mathrm{Uniform}(2,5)$に基づいて生成した乱数を元にモンテカルロ積分を行うと考えればよい。$\mathrm{Uniform}(2,5)$の確率密度関数が$f(x)=1/3, \, 2 \leq x \leq 5$であることからi)と同様に考えることで$E[g(X)]$は下記のように表せる。
$$
\large
\begin{align}
E[g(X)] &= \int_{2}^{5} g(x) \cdot \frac{1}{3} dx \\
&= \frac{1}{3} \int_{2}^{5} g(x) dx = \frac{1}{3} I
\end{align}
$$

よって$\mathrm{Uniform}(2,5)$に基づいて生成された$x_1, \cdots , x_n$元にを$\displaystyle 3 \sum_{i=1}^{n} g(x_i)$を計算することで推定を行うことができる。

import numpy as np

np.random.seed(0)

X = 3.*np.random.rand(10000)+2.
g_X = 3.*np.e**(-X)
g_x = np.e**(-2)-np.e**(-5)

print("Estimated E[g(X)]: {:.3f}".format(np.mean(g_X)))
print("E[g(X)]: {:.3f}".format(np.mean(g_x)))

実行結果

Estimated E[g(X)]: 0.130
E[g(X)]: 0.129

・解説
下記などを参考に作成を行いました。

ボックス・ミュラー法の導出と正規分布に従う乱数の生成

・問題
一様分布に従う乱数が得られる前提で正規分布に従う乱数の生成を行うにあたっては主に「中心極限定理」を用いる手法と「ボックス・ミュラー法」を用いる手法がある。中心極限定理に基づく手法は複数の乱数の平均が中心極限定理に基づいて正規分布に従うことに基づく手法であるが、$1$つのサンプルを作成するにあたって$n=12$個がよく用いられるなどあまり効率的ではない。よって以下では「正規分布に従う乱数の生成」にあたって実用的に用いられることの多い「ボックス・ミュラー法」の原理に関して確認を行う。

一様乱数$U_1 \sim \mathrm{Uniform}(0,1), U_2 \sim \mathrm{Uniform}(0,1)$に対し、下記の変換によって得られる$X, Y$は互いに独立に標準正規分布$\mathcal{N}(0,1)$に従う。
$$
\begin{align}
X &= \sqrt{-2 \log{U_{1}}} \cdot \cos{(2 \pi U_{2})} \\
Y &= \sqrt{-2 \log{U_{1}}} \cdot \sin{(2 \pi U_{2})}
\end{align}
$$

上記に基づいて乱数を生成する手法を「ボックス・ミュラー法」という。ここまでの内容を元に下記の問いに答えよ。

i) 関数電卓やPythonなどを用いて$(U_1,U_2) = (0.1,0.3), (0.8,0.6), (0.2,0.9)$に対応する$(X,Y)$の数値の計算を行え。

ⅱ) 確率変数$X, Y$が$X \sim \mathcal{N}(0,1), Y \sim \mathcal{N}(0,1)$であるとき、確率エレメント$P(x \leq X \leq x+dx, y \leq Y \leq y+dy)$は下記のように表せる。
$$
\large
\begin{align}
& P(x \leq X \leq x+dx, y \leq Y \leq y+dy) \\
&= f(x,y)dxdy = f(x)f(y)dxdy \\
&= \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^2}{2}} dx dy \quad (1)
\end{align}
$$

$(1)$式に対し、$x = r \cos{\theta}, y = r \sin{\theta}$のような変数変換を考えるとき、変数変換のヤコビ行列式$J(R,\Theta)$を計算せよ。

ⅲ) $(1)$式に対し、$x = r \cos{\theta}, y = r \sin{\theta}$を用いて変数変換を行え。

iv) ⅲ)の導出結果に対して$s=r^2$のような変数変換を行い、下記を導出せよ。
$$
\large
\begin{align}
f(x,y)dxdy &= \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^2}{2}} dx dy \quad (1) \\
&= \frac{1}{2 \pi} d \theta \frac{1}{2} e^{-\frac{s}{2}} ds \quad (2)
\end{align}
$$

v) $(2)$式の$\displaystyle \frac{1}{2 \pi}$は一様分布$\mathrm{Uniform}(0,2 \pi)$の確率密度関数に対応する。乱数$\Theta \sim \mathrm{Uniform}(0,2 \pi)$を一様乱数$U_2 \sim \mathrm{Uniform}(0,1)$を元に得る方法を答えよ。

vi) $(2)$式の$\displaystyle \frac{1}{2} e^{-\frac{s}{2}}$は指数分布$\displaystyle \mathrm{Ex} \left( \frac{1}{2} \right)$の確率密度関数に対応する。指数分布$\mathrm{Ex}(\lambda)$の累積分布関数が$F(x)=1-e^{-\lambda x}$であることを元に、逆関数法を用いて乱数$\displaystyle R^2 \sim \mathrm{Ex} \left( \frac{1}{2} \right)$を一様乱数$U_1 \sim \mathrm{Uniform}(0,1)$を元に得る方法を答えよ。

vⅱ)
v)、vi)の結果を元にボックス・ミュラー法の乱数生成が下記で得られることを確認せよ。
$$
\large
\begin{align}
X &= R \cos{\Theta} = \sqrt{-2 \log{U_{1}}} \cdot \cos{(2 \pi U_{2})} \\
Y &= R \sin{\Theta} = \sqrt{-2 \log{U_{1}}} \cdot \sin{(2 \pi U_{2})}
\end{align}
$$

・解答
i)
下記を実行することでそれぞれ計算を行うことができる。

import numpy as np

U_1, U_2 = np.array([0.1, 0.8, 0.2]), np.array([0.3, 0.6, 0.9])
X = np.sqrt(-2*np.log(U_1)) * np.cos(2*np.pi*U_2)
Y = np.sqrt(-2*np.log(U_1)) * np.sin(2*np.pi*U_2)

print(X)
print(Y)

・実行結果

> print(X)
[-0.66313997 -0.54046156  1.45147566]
> print(Y)
[ 2.04093497 -0.39266831 -1.05455879]

ⅱ)
変数変換のヤコビ行列式$J(R,\Theta)$は下記のように計算できる。
$$
\large
\begin{align}
J(R,\theta) &= \left| \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right| \\
&= \left| \begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right| \\
&= r \cos^{2}{\theta} + r \sin^{2}{\theta} = r
\end{align}
$$

ⅲ)
$(3)$式に対して下記のような変数変換を行うことができる。
$$
\large
\begin{align}
f(x,y)dxdy &= \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^2}{2}} dx dy \quad (3) \\
&= \frac{1}{\sqrt{2 \pi}} e^{-\frac{r^2 \cos^{2}{\theta}}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{r^2 \sin^{2}{\theta}}{2}} J(R,\theta) dr d \theta \\
&= \frac{1}{2 \pi} r e^{-\frac{r^2}{2}} dr d \theta
\end{align}
$$

iv)
$\displaystyle r dr = \frac{1}{2} ds$より、$s=r^2$を元に下記のような変数変換を行える。
$$
\large
\begin{align}
f(x,y)dxdy &= \frac{1}{2 \pi} r e^{-\frac{r^2}{2}} dr d \theta \\
&= \frac{1}{2 \pi} e^{-\frac{s}{2}} \cdot \frac{1}{2} ds d \theta \\
&= \frac{1}{2 \pi} d \theta \frac{1}{2} e^{-\frac{s}{2}} ds
\end{align}
$$

v)
$\Theta = 2 \pi U_2$を計算すれば良い。

vi)
累積分布関数に$\displaystyle \lambda=\frac{1}{2}$を代入することで$F(x)=1-e^{-\frac{x}{2}}$が得られる。ここで逆関数法を用いるにあたっては、$\displaystyle U_1=F(x)=1-e^{-\frac{R^2}{2}}$を$R$について解けば良い。
$$
\large
\begin{align}
U_1 &= F(x)=1-e^{-\frac{R^2}{2}} \\
e^{-\frac{R^2}{2}} &= 1-U_1 \\
-\frac{R^2}{2} &= \log{(1-U_1)} \\
R^2 &= -2 \log{(1-U_1)} \\
R &= \sqrt{-2 \log{(1-U_1)}}
\end{align}
$$

vⅱ)
$r$と$\theta$に対応する乱数$R, \Theta$が得られれば、変換式$x = r \cos{\theta}, y = r \sin{\theta}$に基づいて標準正規分布に基づく乱数$X, Y$が下記のように得られる。
$$
\large
\begin{align}
X &= R \cos{\Theta} = \sqrt{-2 \log{(1-U_{1})}} \cdot \cos{(2 \pi U_{2})} \\
Y &= R \sin{\Theta} = \sqrt{-2 \log{(1-U_{1})}} \cdot \sin{(2 \pi U_{2})}
\end{align}
$$

ここで$U_1 \sim \mathrm{Uniform}(0,1)$であることから、上記の式の$1-U_1$を$U_1$で置き換えても式の意味は同じである。よって、下記のようなボックス・ミュラー法の式が得られる。
$$
\large
\begin{align}
X &= R \cos{\Theta} = \sqrt{-2 \log{U_{1}}} \cdot \cos{(2 \pi U_{2})} \\
Y &= R \sin{\Theta} = \sqrt{-2 \log{U_{1}}} \cdot \sin{(2 \pi U_{2})}
\end{align}
$$

・解説
下記の導出を元に作成を行いました。正規分布に基づく乱数は応用先が多い一方で、変数変換$2$回と指数分布への逆関数法の適用など導出がやや複雑なので、何度か演習を行なっておくと良いと思います。

ガンマ分布の形状パラメータ$\alpha$が整数の場合のサンプリング

・問題
ガンマ分布の形状パラメータ$\alpha$が整数の場合は「指数分布に基づく乱数生成」と「ガンマ分布の再生性」の$2$点を元にサンプリングを行うことができる。以下ではこの導出に関して演習形式で取り扱う。

まず前問の「ボックス・ミュラー法の導出と正規分布に従う乱数の生成」より、$Y \sim \mathrm{Ex}(\lambda)$に基づく乱数$Y$は$U \sim \mathrm{Uniform}(0,1)$である一様乱数$U$を用いて下記のように生成できる。
$$
\large
\begin{align}
Y = -\frac{1}{\lambda} \log{U}
\end{align}
$$

上記の指数分布$\mathrm{Ex}(\lambda)$はガンマ分布$\displaystyle \mathrm{Ga} \left( 1,\frac{1}{\lambda} \right)$に一致するので、ガンマ分布$\mathrm{Ga}(1,\beta)$に基づく乱数$X$は下記のように生成できる。
$$
\large
\begin{align}
X = -\beta \log{U} \quad (1)
\end{align}
$$

上記に対し、ガンマ分布の再生性を適用することで、形状パラメータ$\alpha$が整数の場合のガンマ分布の生成を行うことができる。ここまでの内容を元に以下の問いに答えよ。

i) ガンマ分布$\mathrm{Ga} (\alpha,\beta)$の確率密度関数$f(x)$を$x,\alpha,\beta$などを用いて表せ。また、$\alpha=1,\beta=1/\lambda$を代入すると指数分布$\mathrm{Ex}(\lambda)$の確率密度関数に一致することを確かめよ。

ⅱ) ガンマ分布$\mathrm{Ga} (\alpha,\beta)$のモーメント母関数を$m(t)=E[e^{tX}]$とおくとき、$m(t)$を導出せよ。

ⅲ) ⅱ)で導出を行なったモーメント母関数を元にガンマ分布の再生性を示せ。

iv) ⅲ)で示したガンマ分布の再生性を元に、下記が成立する。
$$
\begin{align}
X_1 + X_2 + \cdots X_n \sim \mathrm{Ga}(n,\beta)
\end{align}
$$

$(1)$式に基づいて一様乱数を用いて$\mathrm{Ga}(n,\beta)$に従う乱数$\displaystyle Z = \sum_{i=1}^{n} X_i$を生成する式を答えよ。

v) iv)の結果をガンマ分布の確率密度関数の形状やガンマ分布$\mathrm{Ga}(\alpha,\beta)$の平均が$\alpha \beta$であることなどに基づいて簡単に解釈せよ。

・解答
i)
ガンマ分布$\mathrm{Ga} (\alpha,\beta)$の確率密度関数$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} \right)}
\end{align}
$$

上記に$\alpha=1, \beta=1/\lambda$を代入すると$\Gamma(\alpha)=1$より下記のように変形できる。
$$
\large
\begin{align}
f(x) &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} \right)} \\
&= \frac{1}{(1/\lambda)^{1} \Gamma(1)} x^{1-1} \exp{\left( -\frac{x}{1/\lambda} \right)} \\
&= \lambda e^{-\lambda x}
\end{align}
$$

上記は指数分布$\mathrm{Ex}(\lambda)$の確率密度関数に一致する。

ⅱ)
ガンマ分布$\mathrm{Ga} (\alpha,\beta)$のモーメント母関数$m(t)=E[e^{tX}]$は下記のように導出できる。
$$
\large
\begin{align}
m(t) &= E[e^{tX}] = \int_{0}^{\infty} e^{tx} f(x) dx \\
&= \int_{0}^{\infty} \exp{(tx)} \times \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} \right)} dx \\
&= \int_{0}^{\infty} \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} + t \beta \right)} dx \\
&= \int_{0}^{\infty} \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta/(1 – t \beta)} \right)} dx \\
&= \frac{1}{(1 – t \beta)^{\alpha}} \int_{0}^{\infty} \frac{(1 – t \beta)^{\alpha}}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta/(1 – t \beta)} \right)} dx \\
&= \frac{1}{(1 – t \beta)^{\alpha}} \times 1 = \frac{1}{(1-t \beta)^{\alpha}}
\end{align}
$$

ⅲ)
$X_1 \sim \mathrm{Ga} (\alpha_1,\beta), X_2 \sim \mathrm{Ga} (\alpha_2,\beta)$のとき、$m_{X_1+X_2}(t) = E[e^{t(X_1+X_2)}]$は下記のように計算できる。
$$
\large
\begin{align}
m_{X_1+X_2}(t) &= E[e^{t(X_1+X_2)}] = E[e^{tX_1}] E[e^{tX_2}] \\
&= \frac{1}{(1-t \beta)^{\alpha_1}} \times \frac{1}{(1-t \beta)^{\alpha_2}} \\
&= \frac{1}{(1-t \beta)^{\alpha_1+\alpha_2}}
\end{align}
$$

モーメント母関数と確率分布の$1$対$1$対応より、$X_1+X_2 \sim \mathrm{Ga} (\alpha_1+\alpha_2,\beta)$が成立するのでガンマ分布の再生性が示される。

iv)
$U_1, U_2, \cdots U_n \sim \mathrm{Uniform}(0,1), \, \mathrm{i.i.d.,}$のとき、$\mathrm{Ga}(n,\beta)$に従う乱数$\displaystyle Z = \sum_{i=1}^{n} X_i$は下記の式により生成できる。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i &= -\sum_{i=1}^{n} \beta\log{U_i} \\
&= -\beta \log{ \left[ \prod_{i=1}^{n} U_i \right] }
\end{align}
$$

v)

import math
import numpy as np
import matplotlib.pyplot as plt

alpha = np.array([2., 3., 5., 7., 10.])
beta = 1.

x = np.arange(0., 15.1, 0.1)

for i in range(alpha.shape[0]):
    f_x = x**(alpha[i]-1) * np.e**(-x/beta) /(beta**alpha[i] * math.factorial(alpha[i]-1))
    plt.plot(x,f_x,label="alpha: {}, beta: {}".format(alpha[i],beta))

plt.legend()
plt.show()

実行結果

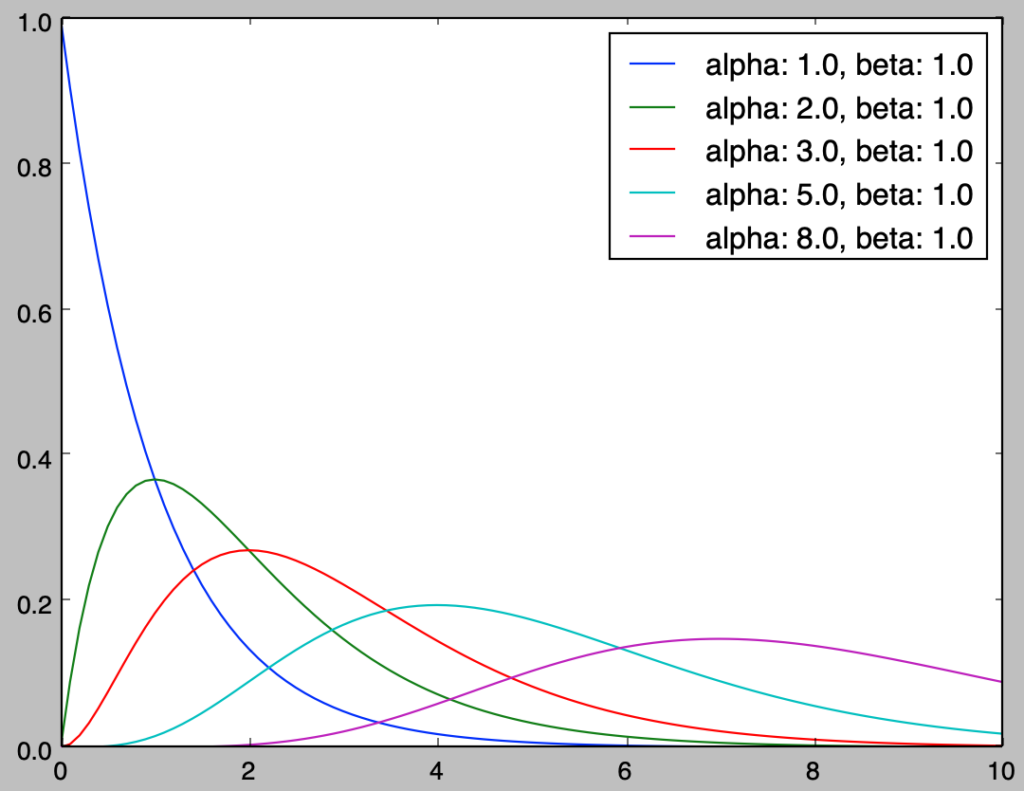
上図の青の確率密度関数に基づいて生成される乱数の和によってその他のガンマ分布の乱数が生成されると直感的に解釈することができる。ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の平均は$\alpha \beta$であることに基づいても同様の解釈ができる。

・解説
下記などに基づいて問題の作成を行いました。

ガンマ分布の形状パラメータ$\alpha$が$($整数$+1/2)$の場合のサンプリング

・問題
前問の「ガンマ分布の形状パラメータ$\alpha$が整数の場合のサンプリング」より、ガンマ分布の形状パラメータ$\alpha$が整数の場合は一様乱数$U_1, U_2, \cdots U_n \sim \mathrm{Uniform}(0,1), \, \mathrm{i.i.d.,}$を用いることで、$\mathrm{Ga}(n,\beta)$に従う乱数$\displaystyle \sum_{i=1}^{n} X_i$を下記のように生成できる。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i &= -\sum_{i=1}^{n} \beta\log{U_i} \\
&= -\beta \log{ \left[ \prod_{i=1}^{n} U_i \right] }
\end{align}
$$

この問題では以下、形状パラメータ$\alpha$が整数でない場合への拡張にあたって$($整数$+1/2)$の取り扱いに関して演習形式で確認を行う。以下の問いにそれぞれ答えよ。
i) ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の確率密度関数を$f(x)$とおくと$f(x)$は下記のように表すことができる。
$$
\begin{align}
f(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} \right)}
\end{align}
$$

上記を元に$\mathrm{Ga}(1/2,2)$の確率密度関数$f_1(x)$と$\mathrm{Ga}(1/2,\beta)$の確率密度関数$f_2(y)$をそれぞれ答えよ。

ⅱ) i)で確認した$f_1(x), f_2(y)$の$\exp$の項に着目し、$x$から$y$の変数変換の式を作成せよ。
ⅲ) ⅱ)の式を元に$f_1(x)$の変数変換を行い、$f_2(y)$を導出せよ。
iv) $f_1(x)$は自由度$1$の$\chi^2$分布$\chi^2(1)$の確率密度関数であるので、$Z \sim \mathcal{N}(0,1)$のとき$Z^2 \sim \mathrm{Ga}(1/2,2)$が成立すると考えることができる。$\mathrm{Ga}(1/2,\beta)$に従う確率変数を$\beta, Z^2$などを用いて表せ。
v) ガンマ分布の再生性に基づいて乱数$U_1, U_2, \cdots U_n \sim \mathrm{Uniform}(0,1), \, \mathrm{i.i.d.,}$と$Z \sim \mathcal{N}(0,1)$を用いて$\displaystyle \mathrm{Ga} \left( n+\frac{1}{2},\beta \right)$に従う乱数を生成する式を答えよ。

・解答
i)
確率密度関数$f_1(x), f_2(y)$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
f_1(x) &= \frac{1}{\displaystyle 2^{\frac{1}{2}} \Gamma \left( \frac{1}{2} \right)} x^{\frac{1}{2}-1} \exp{\left( -\frac{x}{2} \right)} \\
f_2(y) &= \frac{1}{\displaystyle \beta^{\frac{1}{2}} \Gamma \left( \frac{1}{2} \right)} y^{\frac{1}{2}-1} \exp{\left( -\frac{y}{\beta} \right)}
\end{align}
$$

ⅱ)
変数変換によって$x$を$y$の式で置き換えるので、$\displaystyle \frac{x}{2} = \frac{y}{\beta}$が成立する必要がある。よって下記の変数変換の式が得られる。
$$
\large
\begin{align}
\frac{x}{2} &= \frac{y}{\beta} \\
x &= \frac{2y}{\beta}
\end{align}
$$

ⅲ)
$\displaystyle x = \frac{2y}{\beta}$より、$\displaystyle \frac{dx}{dy} = \frac{2}{\beta}$が成立する。よって、$f_2(y)$は$f_1(x)$の変数変換に基づいて下記のように導出できる。
$$
\large
\begin{align}
f_2(y) &= f_1(x) \left| \frac{dx}{dy} \right| \\
&= f_1 \left( \frac{2y}{\beta} \right) \cdot \frac{2}{\beta} \\
&= \frac{1}{\displaystyle 2^{\frac{1}{2}} \Gamma \left( \frac{1}{2} \right)} \left( \frac{2y}{\beta} \right)^{\frac{1}{2}-1} \exp{\left( -\frac{1}{\cancel{2}} \cdot \frac{\cancel{2}y}{\beta} \right)} \cdot \frac{2}{\beta} \\
&= \frac{\beta^{\frac{1}{2}}}{\displaystyle \cancel{2} \Gamma \left( \frac{1}{2} \right)} y^{\frac{1}{2}-1} \exp{\left( -\frac{y}{\beta} \right)} \cdot \frac{\cancel{2}}{\beta} \\
&= \frac{1}{\displaystyle \beta^{\frac{1}{2}} \Gamma \left( \frac{1}{2} \right)} y^{\frac{1}{2}-1} \exp{\left( -\frac{y}{\beta} \right)}
\end{align}
$$

上記はi)で確認した$f_2(x)$に一致する。

iv)
ⅱ)の式に基づいて$\displaystyle y = \frac{\beta}{2} x$より、下記のように考えることができる。
$$
\large
\begin{align}
\frac{\beta}{2} Z^2 \sim \mathrm{Ga}(1/2,\beta)
\end{align}
$$

v)
$\displaystyle \mathrm{Ga} \left( n+\frac{1}{2},\beta \right)$に従う乱数を生成する式は下記のように得られる。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i + \frac{\beta}{2} Z^2 = -\beta \log{ \left[ \prod_{i=1}^{n} U_i \right] } + \frac{\beta}{2} Z^2
\end{align}
$$

・解説
下記などを元に作成を行いました。

モンテカルロ法による推定と必要なサンプル数

・問題
モンテカルロ法は乱数を用いて数値計算を行う手法である。この問題では以下、モンテカルロ法を用いた円周率$\pi$の推定法に関して確認し、推定結果の標準偏差に対応する必要なサンプル数に関して考察を行う。下記の問いにそれぞれ答えよ。

i) 原点$(0,0)$を中心とする半径$1$の単位円を考えるとき、第$1$象限の面積を円周率$\pi$を用いて表せ。
ⅱ) $X \sim \mathrm{Uniform}(0,1), \, Y \sim \mathrm{Uniform}(0,1)$のように一様分布$\mathrm{Uniform}(0,1)$に基づく乱数$(X,Y)$を発生させる。このとき$X^2+Y^2 \leq 1$である確率がi)の結果に等しいことを確認せよ。
ⅲ) $X_i \sim \mathrm{Uniform}(0,1), \, Y_i \sim \mathrm{Uniform}(0,1)$を元に乱数$(X_i,Y_i), \, i=1,2,\cdots,N$を発生させるとき、$X_i^2+Y_i^2 \leq 1$である乱数が$M$個観測されたと仮定する。このとき、$M, N$を用いて円周率$\pi$の推定量$\hat{\pi}$を表せ。
iv) $\displaystyle M \sim \mathrm{Bin} \left( N,\frac{\pi}{4} \right)$のように確率変数$M$が二項分布に従うことに基づいて$V[M]$を計算せよ。
v) $\hat{\pi}$の分散$\displaystyle V[\hat{\pi}] = V \left[ \frac{4M}{N} \right]$を$\pi,N$を用いて表し、$SD[\hat{\pi}]=\sqrt{V[\hat{\pi}]} \leq 0.01$が成立する際の$N$の最小値を計算せよ。ただし$\pi \simeq 3.14$を用いて良い。

・解答
i)
半径$1$の円の面積が$\pi$であることから、単位円の第$1$象限の面積は$\displaystyle \frac{\pi}{4}$である。

ⅱ)

上図の緑の正方形の$1$辺の長さは$1$であるので、正方形の面積は$1$である。i)より円の面積は$\displaystyle \frac{\pi}{4}$であることから$X^2+Y^2 \leq 1$である確率は$\displaystyle \frac{\pi}{4}$に一致する。

ⅲ)
$\displaystyle \frac{M}{N} = \frac{\hat{\pi}}{4}$であるので、推定量$\hat{\pi}$は下記のように表せる。
$$
\large
\begin{align}
\frac{M}{N} &= \frac{\hat{\pi}}{4} \\
\hat{\pi} &= \frac{4M}{N}
\end{align}
$$

iv)
確率変数$X$が$X \sim \mathrm{Bin}(n,p)$のように二項分布$\mathrm{Bin}(n,p)$に従うとき、$V[X]=np(1-p)$である。よって$V[M]$は下記のように表せる。
$$
\large
\begin{align}
V[M] = N \cdot \frac{\pi}{4} \cdot \left( 1 – \frac{\pi}{4} \right)
\end{align}
$$

v)
$\displaystyle V[\hat{\pi}] = V \left[ \frac{4M}{N} \right]$より、$V[\hat{pi}]$は下記のように計算できる。
$$
\large
\begin{align}
V[\hat{\pi}] &= V \left[ \frac{4M}{N} \right] = \frac{4^2}{N^2} V[M] \\
&= \frac{4^2}{N^2} \times N \cdot \frac{\pi}{4} \cdot \left( 1 – \frac{\pi}{4} \right) \\
&= \frac{\pi(4-\pi)}{N}
\end{align}
$$

よって、$SD[\hat{\pi}]=\sqrt{V[\hat{\pi}]} \leq 0.01$は下記のように表せる。
$$
\large
\begin{align}
SD[\hat{\pi}] & \leq 0.01 \\
\sqrt{V[\hat{\pi}]} & \leq 0.01 \\
\frac{\pi(4-\pi)}{N} & \leq 0.01^2 \\
N & \geq 10000 \times 3.14 \times (4-3.14) \\
N & \geq 27004
\end{align}
$$

上記より$N$の最小値は$27004$であると考えられる。

・解説
$\pi$が推定対象であることからv)では$\pi \simeq 3.14$のように小数点$2$桁までを計算に用いました。

下記などに基づいて問題の作成を行いました。

参考書籍

・自然科学の統計学(東京大学出版)

自然科学の統計学 (基礎統計学)

3,190円(11/10 17:47時点)

Amazon

基本問題

母平均の検定① 母分散既知の場合

・問題
同一の確率分布から独立に標本$x_1, x_2, …, x_n$が得られたとする。このとき下記の問題に答えよ。
i) 標本平均$\bar{x}$を標本$x_1, x_2, …, x_n$の式で表せ。
ⅱ) 標本$x_i$の母分散$\sigma^2$を既知とするとき、中心極限定理より$\bar{x}$の母平均を$\mu$とすると$N(\mu, \sigma^2/n)$に従うと考えることができる。
このとき$\bar{x}$の標準化を行い、標準正規分布$N(0,1)$に従う指標を求めよ。
ⅲ) $\bar{x}=20, \mu=19.5, \sigma=1, n=9$のとき、有意水準95％で帰無仮説$H_0: \mu=19.5$の検定を行え。
iv) $\bar{x}=20, \sigma=1, n=9$のとき、$\mu$の95％区間を求めよ。
v) iv)で求めた区間を0.2以下にする最小のサンプル数$n$の値を求めよ。

・解答
i)
標本平均$\bar{x}$は下記のように表すことができる。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{n} (x_1 + x_2 + … + x_n) \\
&= \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align}
$$

ⅱ)
$\bar{x}$の標準化は下記のように行うことができる。
$$
\large
\begin{align}
z = \frac{\bar{x}-\mu}{\sigma/\sqrt{n}}
\end{align}
$$

ⅲ)
ⅱ)で求めた式に$\bar{x}=20, \mu=19.5, \sigma=1, n=9$を代入すると下記のようになる。
$$
\large
\begin{align}
z &= \frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \\
&= \frac{20-19.5}{1/\sqrt{9}} \\
&= 0.5 \times 3 \\
&= 1.5
\end{align}
$$
$z=1.5<1.96=z_{\alpha=0.025}$より、帰無仮説$H_0: \mu=19.5$は棄却できない。

iv)
母平均$\mu$の95％区間は下記のように計算できる。
$$
\large
\begin{align}
z_{\alpha=0.975} \leq &\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \leq z_{\alpha=0.025} \\
-1.96 \leq &\frac{20-\mu}{1/\sqrt{9}} \leq 1.96 \\
-\frac{1.96}{3} \leq &20-\mu \leq \frac{1.96}{3} \\
-\frac{1.96}{3} \leq &\mu-20 \leq \frac{1.96}{3} \\
20 – \frac{1.96}{3} \leq &\mu \leq 20 + \frac{1.96}{3} \\
19.3… \leq &\mu \leq 20.6…
\end{align}
$$

v)
$\displaystyle z_{\alpha=0.025} \frac{\sigma^2}{\sqrt{n}} = \frac{1.96}{\sqrt{n}} \leq 0.1$となる$n$を求めれば良い。
$$
\large
\begin{align}
\frac{1.96}{\sqrt{n}} &\leq 0.1 \\
1.96 &\leq 0.1\sqrt{n} \\
19.6 &\leq \sqrt{n} \\
19.6^2 &\leq n \\
384.1… &\leq n
\end{align}
$$
上記より、95％区間を0.2以下にする最小のサンプル数$n$は385である。

母平均の検定② 母分散未知の場合

・問題
同一の確率分布から独立に標本$x_1, x_2, …, x_n$が得られたとする。このとき下記の問題に答えよ。
i) 不偏標本分散$s^2$を標本$x_1, x_2, …, x_n$の式で表せ。
ⅱ) 標本$x_i$の母分散が未知のとき、$\displaystyle t = \frac{\bar{x}-\mu}{s/\sqrt{n}}$はどのような分布に従うか。また、ここで取り扱う分布と標準正規分布の違いを述べよ。
ⅲ) $\bar{x}=20, s=1, n=9$のとき、有意水準95％で帰無仮説$H_0: \mu=19$の検定を行え。
iv) $\bar{x}=20, s=1, n=9$のとき、$\mu$の95％区間を求めよ。
v) 概ね同じような値に基づいて区間推定や検定を行う場合、母分散既知の場合と母分散未知の場合の結果はどのように異なるか簡単に説明せよ。

・解答
i)
不偏標本分散$s^2$は下記のように表すことができる。
$$
\large
\begin{align}
s^2 &= \frac{1}{n-1} ((x_1-\bar{x})^2 + (x_2-\bar{x})^2 + … + (x_n-\bar{x})^2) \\
&= \frac{1}{n-1} \sum_{i=1}^{n} (x_i-\bar{x})^2
\end{align}
$$

ⅱ)
$\displaystyle t = \frac{\bar{x}-\mu}{s/\sqrt{n}}$は自由度$n-1$の$t$分布$t(n-1)$に従う。

ⅲ)
ⅱ)で求めた式に$\bar{x}=20, \mu=19, s=1, n=9$を代入すると下記のようになる。
$$
\large
\begin{align}
t &= \frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \\
&= \frac{20-19}{1/\sqrt{9}} \\
&= 1 \times 3 \\
&= 3
\end{align}
$$
$t=3<2.306=t_{\alpha=0.025}(8)=t_{\alpha=0.025}(9-1)$より、帰無仮説$H_0: \mu=19$は棄却できる。

iv)
母平均$\mu$の95％区間は下記のように計算できる。
$$
\large
\begin{align}
t_{\alpha=0.975}(8) \leq &\frac{\bar{x}-\mu}{s/\sqrt{n}} \leq t_{\alpha=0.025}(8) \\
-2.306 \leq &\frac{20-\mu}{1/\sqrt{9}} \leq 2.306 \\
-\frac{2.306}{3} \leq &20-\mu \leq \frac{2.306}{3} \\
-\frac{2.306}{3} \leq &\mu-20 \leq \frac{2.306}{3} \\
20 – \frac{2.306}{3} \leq &\mu \leq 20 + \frac{2.306}{3} \\
19.23… \leq &\mu \leq 20.76…
\end{align}
$$

v)
不偏標本分散$s^2$が母分散$\sigma^2$と概ね等しいと考えられる場合、$t$分布の方が標準正規分布よりばらつきの大きい分布となる。よって、iv)の結果は標準正規分布を用いた際よりもやや範囲が広い結果となった。
一方で、サンプル数が増えるに伴い自由度が増えるにつれて、$t$分布は正規分布に近づく。ⅲ)、iv)で用いた自由度8の場合は$t_{\alpha=0.025}(8)=2.306$であるのに対して、自由度120の場合は$t_{\alpha=0.025}(120)=1.98$であり、標準正規分布の$z_{\alpha=0.025}=1.96$に近い値となる。

・解説
$t$分布の式は複雑ですが、v)で取り扱ったように、$t$分布は標準正規分布との対応で抑えておくと理解しやすいと思います。

両側検定と片側検定

・問題
標準正規分布の上側確率を$p$とする点を$z_{\alpha=p}$のように表すと考える。以下の問題に答えよ。
i) $z_{\alpha=0.005}, z_{\alpha=0.01}, z_{\alpha=0.025}, z_{\alpha=0.05}, z_{\alpha=0.1}, z_{\alpha=0.2}$の値を標準正規分布の確率分布表からそれぞれ読み取れ。
ⅱ) $z_{\alpha=0.995}, z_{\alpha=0.99}, z_{\alpha=0.975}, z_{\alpha=0.95}, z_{\alpha=0.9}, z_{\alpha=0.8}$はi)で求めた値とどのような関係があるか答えよ。
ⅲ) 95％の両側検定を行う場合に用いる$z_{\alpha=p}$を2つ答えよ。
iv) 定数$c$を用いて対立仮説を$H_1:\mu<c$と表せるかを考える場合に用いる$z_{\alpha=p}$を答えよ。有意水準はⅲ)と同じく95％で考えるものとする。
v) $\bar{x}=14, c=15, \sigma^2=1, n=9$のとき、iv)の検定の結果を述べよ。

・解答
i)
標準正規分布の表から、下記のように読み取ることができる。
$$
\large
\begin{align}
z_{\alpha=0.005} &= 2.58 \\
z_{\alpha=0.01} &= 2.33 \\
z_{\alpha=0.025} &= 1.96 \\
z_{\alpha=0.05} &= 1.64 \\
z_{\alpha=0.1} &= 1.28 \\
z_{\alpha=0.2} &= 0.84
\end{align}
$$

ⅱ)
下記のように考えればよい。
$$
\large
\begin{align}
z_{\alpha=0.995} &= -z_{\alpha=0.005} = -2.58 \\
z_{\alpha=0.99} &= -z_{\alpha=0.01} = -2.33 \\
z_{\alpha=0.975} &= -z_{\alpha=0.025} = -1.96 \\
z_{\alpha=0.95} &= -z_{\alpha=0.05} = -1.64 \\
z_{\alpha=0.9} &= -z_{\alpha=0.1} = -1.28 \\
z_{\alpha=0.8} &= -z_{\alpha=0.2} = -0.84
\end{align}
$$

ⅲ)
95％の両側検定では、$z_{\alpha=0.975}$と$z_{\alpha=0.025}$の間に標準化した値の$z$が含まれるかどうかで検定を行う。含まれない場合は帰無仮説$H_0:\mu=c$を棄却し、対立仮説$H_1:\mu \neq c$を採択する。

iv)
95％の片側検定かつ、対立仮説$H_1$が$\mu<c$のため、$z_{\alpha=0.95}$よりも$z$が大きいか小さいかを考える。$z<z_{\alpha=0.95}=-1.64$の場合は帰無仮説$H_0:\mu=c$を棄却し、対立仮説の$H_1:\mu<c$を採択する。

v)
標準化を考えるにあたって、下記のように$z$を計算する。
$$
\large
\begin{align}
z &= \frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \\
&= \frac{14-15}{1/\sqrt{9}} \\
&= -3 < -1.64 = z_{\alpha=0.95}
\end{align}
$$
上記より、帰無仮説$H_0:\mu=15$は棄却され、対立仮説の$H_1:\mu<15$が採択される。

・解説
両側検定と片側検定については基本的な事項であるため流されやすいが、特に片側検定はわからなくなりやすいので注意しておくと良いです。基本事項を抑えつついくつか演習問題を解くことで、なるべく慣れておくのが良いと思います。

発展問題

$\chi^2$検定

適合度の検定

$F検定$

参考書籍

・基礎統計学Ⅰ 統計学入門(東京大学出版会)

・第12章解答
https://www.hello-statisticians.com/explain-books-cat/toukeigakunyuumon-akahon/ch12_practice.html

基本問題

確率の加法定理

・問題
i) $P(A \cup B)$を$P(A), P(B), P(A \cap B)$を用いて表せ。
ⅱ) $P(A \cup B)$を$P(A)+P(B)$で表せるのはどのような場合か。
ⅲ) $P(A)=0.4, P(B)=0.3, P(A \cap B)=0.2$の時の、$P(A \cup B)$の値を求めよ。

・解答
i)
$P(A \cup B)$は下記のように計算することができる。
$$
\large
\begin{align}
P(A \cup B) = P(A) + P(B) – P(A \cap B)
\end{align}
$$

ⅱ)
AとBがそれぞれが同時に起こらない排反事象である時に$P(A \cup B)=P(A)+P(B)$が成立する。

ⅲ)
i)の式に基づいて下記のように計算できる。
$$
\large
\begin{align}
P(A \cup B) &= P(A) + P(B) – P(A \cap B) \\
&= 0.4 + 0.3 – 0.2 \\
&= 0.5
\end{align}
$$

・解説
基本事項ではありますが、表記に慣れていないうちは難しく見えると思いますので、難しく見える場合はなるべく演習を多めに取り組むと良いと思います。

条件付き確率と独立

・問題
事象Bが起こった上で事象Aが起こる確率を条件付き確率と呼び、$P(A|B)$のように表す。以下、条件付き確率に関する下記の問題に答えよ。
i) 条件付き確率$P(A|B)$を$P(B), P(A \cap B)$を用いて表せ。
ⅱ) i)で求めた$P(A|B)$の式はAとBが独立である時と独立でない時にどのように変化するかを述べよ。
ⅲ) $P(B)=0.5, P(A \cap B)=0.25$の時の条件付き確率$P(A|B)$の値を求めよ。

・解答
i)
条件付き確率$P(A|B)$は下記のように表すことができる。
$$
\large
\begin{align}
P(A|B) = \frac{P(A \cap B)}{P(B)}
\end{align}
$$

ⅱ)
事象Aと事象Bが独立である場合、$P(A \cap B) = P(A)P(B)$となるので、これを下記のようにi)の式に代入する。
$$
\large
\begin{align}
P(A|B) &= \frac{P(A \cap B)}{P(B)} \\
&= \frac{P(A)P(B)}{P(B)} \\
&= P(A)
\end{align}
$$
よって条件付き確率$P(A|B)$はAとBが独立な場合は、$P(A)$に一致する。

ⅲ)
i)の式に基づいて下記のように計算できる。
$$
\large
\begin{align}
P(A|B) &= \frac{P(A \cap B)}{P(B)} \\
&= \frac{0.25}{0.5} \\
&= 0.5
\end{align}
$$

・解説
基本事項ではありますが、表記に慣れていないうちは難しく見えると思いますので、難しく見える場合はなるべく演習を多めに取り組むと良いと思います。

発展問題

チェビシェフの不等式の導出とその理解

・問題
$$
\large
\begin{align}
P(|X-\mu| \geq c) \leq \frac{\sigma^2}{c^2} \quad (1)
\end{align}
$$
$(1)$式で表したチェビシェフの不等式は大数の法則などに用いられるが、唐突に式だけ出てきてもわからないので以下ではチェビシェフの不等式の導出とその理解に関して取り扱う。
$$
\large
\begin{align}
P(X \geq c) \leq \frac{E[X]}{c} \quad (2)
\end{align}
$$
$(1)$式のチェビシェフの不等式を導出するにあたっては$(2)$式で表したマルコフの不等式の導出を行なったのちに、マルコフの不等式を用いてチェビシェフの不等式を導出するとわかりやすい。

ここまでの内容を元に以下の問いに答えよ。
i) 確率変数$Y$を下記のように定義する。
$$
\large
\begin{align}
Y &= 0, \quad if \quad X < c \\
&= c, \quad if \quad X \geq c
\end{align}
$$
このとき全ての$Y$に関して$Y \leq X$であるかつ、$E[Y] \leq E[X]$が成立することを確認せよ。
ⅱ) $Y$が$0$か$c$の値のみを取ることを元に、$E[Y]=cP(Y=c)$が成立することを確認せよ。
ⅲ) i)とⅱ)よりマルコフの不等式を表す$(2)$式が成立することを確認せよ。
iv) マルコフの不等式を直感的に解釈せよ。
v) 有限な確率変数$X$に関して$E[X]=\mu, V[X]=\sigma^2$が成立するとき、非負の確率変数$Y=(X-\mu)^2$と閾値$c^2$に関してマルコフの不等式が成立することを利用することで$(1)$式を導出せよ。
vi) チェビシェフの不等式を直感的に解釈せよ。

・解答
i)
$X \geq 0$における$Y=X$の直線を考えた際に、$X=0,c$は直線上の点で$Y=X$となり、その他の点では$Y$が$X$を下回ることが確認できる。これにより任意の点で$Y \leq X$で、同時に期待値に関して$E[Y] \leq E[X]$も成立する。

ⅱ)
$E[Y]=cP(Y=c)$は下記のように示すことができる。
$$
\large
\begin{align}
E[Y] &= 0 \times P(Y=0) + c \times P(Y=c) \\
&= c P(Y=c) \\
&= c P(X \geq c)
\end{align}
$$

ⅲ)
$E[Y]=cP(Y=c), E[Y] \leq E[X]$より下記が成立する。
$$
\large
\begin{align}
cP(Y=c) &= E[Y] \leq E[X] \\
cP(Y=c) & \leq E[X]
\end{align}
$$
$P(Y=c)=P(X \geq c)$より下記が成立する。
$$
\large
\begin{align}
cP(Y=c) & \leq E[X] \\
cP(X \geq c) & \leq E[X] \\
P(X \geq c) & \leq \frac{E[X]}{c}
\end{align}
$$

iv)
$\displaystyle P(X \geq c) \leq \frac{E[X]}{c}$で表されるマルコフの不等式は、期待値$E[X]$が大きい場合、上側確率$P(X \geq c)$の上限も大きくなる一方で、閾値$c$が大きくなると上側確率$P(X \geq c)$の上限が小さくなると解釈することができる。

v)
$c^2P(Y \geq c^2) \leq E[Y]$を変形することでチェビシェフの不等式の導出を行う。
$$
\large
\begin{align}
c^2P(Y \geq c^2) & \leq E[Y] \\
P(Y \geq c^2) & \leq \frac{E[Y]}{c^2} \\
P((X-\mu)^2 \geq c^2) & \leq \frac{E[(X-\mu)^2]}{c^2} \\
P(|X-\mu| \geq c) & \leq \frac{V[X]}{c^2} \\
P(|X-\mu| \geq c) & \leq \frac{\sigma^2}{c^2}
\end{align}
$$

vi)
有限な確率変数$X$に関して$c$を閾値に設定する場合の期待値$E[X]$を中心と考えた際の両端の確率$P(|X-E[X]| \geq c)$は、$\displaystyle \frac{V[X]}{c^2}$よりも小さくなる。
これは、確率変数の分散$V[X]$が大きい場合、$E[X]$を中心に考えた際の両端の確率$P(|X-E[X]| \geq c)$の上限も大きくなる一方で、閾値$c$が大きくなると両端の確率$P(|X-E[X]| \geq c)$の上限が小さくなると解釈できる。

・解説
https://www.hello-statisticians.com/explain-terms-cat/law_of_large_numbers1.html
上記を元に作成を行いました。統計学を考えるにあたっては、大数の法則の導出や確率収束・一致性の定義にも関わるトピックであるので、なるべく抑えておくと良いと思います。

確率変数、統計量と推定量・推定値

・問題
確率変数$X$は統計学の参考書で当たり前のように出てくるが、確率関数$p(x)$や確率密度関数$f(x)$の際には$x$が用いられる一方で、確率変数は$X$が用いられるなど使い分けが大変わかりにくく、「現代数理統計学」の$2.1$節に同様の指摘がある。そこで以下では演習形式で使い分けがわかるように確認を行う。

確率変数$X$を考える上で注意が必要なのは、確率変数$X$は単に変数の表記であり、具体的な値を示す場合は$1$のような数を用いて$X=1$のように示すことである。例えばサイコロの目が$1$である確率は$P(X=1)$のように表すことができる。

ここまではまだ理解できるが、確率変数の実現値を変数のように取り扱いたい場合は$X$が実現値に用いられないことでさらにわかりにくくなる。たとえばサイコロの場合は$X=x, \, x \in \{1,2,3,4,5,6\}$のように表すことができるが、これだけでも難しく見えると思われる。

以下では具体的な事例を元に確率変数$X$の使用事例の確認を行う。また、集合論の基本的な表記も合わせて抑えておく方が望ましいので、同時に取り扱う。

これまでの内容を元に、以下の問いに答えよ。
i) $x$を$1$以上$10$以下の偶数とするとき、$x \in \{1,2,3,4,5,6\}$のような表記を用いて$x$を表せ。ただし、要素をそのまま書き下すだけで十分である。
ⅱ) $X$をコイン投げに関する確率変数と考え、表に$1$、裏に$0$が対応するとき、サイコロに関する$X=x, \, x \in \{1,2,3,4,5,6\}$と同様な記法を用いて、コイン投げに関する$X$について表記せよ。
ⅲ) サイコロに関するそれぞれの目が出る確率は下記のように表記できる。
$$
\begin{align}
P(X=x) = \frac{1}{6}, \quad x \in \{1,2,3,4,5,6\}
\end{align}
$$
上記と同様にⅱ)のコイン投げの場合を表せ。
iv) 確率関数$p(x)$と確率密度関数$f(x)$は下記のように定義できる。
$$
\begin{align}
p(x) &= P(X=x) \\
f(x) &= \lim_{\epsilon \to 0} \frac{P(x \leq X \leq x + \epsilon)}{\epsilon}
\end{align}
$$
上記を参考に、確率関数$p(x)$と確率密度関数$f(x)$の違いは何かを答えよ。
v) 累積分布関数を$F(x)$とおく際に、iv)を元に下記が導出できることを確認せよ。
$$
\begin{align}
f(x) = F'(x)
\end{align}
$$
vi) 確率変数列$X_1,X_2,…,X_n$に対して、下記のように統計量$T$を定義すると考える。
$$
\begin{align}
T = T(X_1,X_2,…,X_n)
\end{align}
$$
このとき$\bar{X}, S^2$を下記のように定義する。
$$
\begin{align}
\bar{X} &= \frac{1}{n} \sum_{i=1}^{n} X_i \\
S^2 &= \frac{1}{n} \sum_{i=1}^{n} (X_i-\bar{X})^2
\end{align}
$$
$T=\bar{X}$であるとき、観測値$X_1=x_1, X_2=x_2, …, X_n=x_n$に関する$T$の実現値$t$を求めよ。
vⅱ) vi)に関連して推定量(estimator)と推定値(estimate)の慣用的な区別について答えよ。

・解答
i)
$x$は下記のように表すことができる。
$$
\large
\begin{align}
x \in \{2,4,6,8,10\}
\end{align}
$$

ⅱ)
コイン投げに関する$X$は下記のように表すことができる。
$$
\large
\begin{align}
X=x, \quad x \in \{0,1\}
\end{align}
$$

ⅲ)
確率$P(X=x)$は下記のように表すことができる。
$$
\large
\begin{align}
P(X=x) = \frac{1}{2}, \quad x \in \{0,1\}
\end{align}
$$

iv)
確率関数$p(x)$は確率変数$X$が離散である場合、確率密度関数$f(x)$は確率変数$X$が連続である際にそれぞれ用いられる。

v)
累積分布関数の定義式や微分の定義式に基づいて、下記のように導出を行うことができる。
$$
\large
\begin{align}
f(x) &= \lim_{\epsilon \to 0} \frac{P(x \leq X \leq x + \epsilon)}{\epsilon} \\
&= \lim_{\epsilon \to 0} \frac{F(x + \epsilon)-F(x)}{\epsilon} \\
&= F'(x)
\end{align}
$$

vi)
$T$の実現値$t$は下記のように導出することができる。
$$
\begin{align}
t &= T(X_1=x_1,X_2=x_2,…,X_n=x_n) \\
&= \frac{1}{n} \sum_{i=1}^{n} x_i \\
&= \bar{x}
\end{align}
$$

vⅱ)
推定量$T=T(X_1,X_2,…,X_n)$と推定値$t=T(X_1=x_1,X_2=x_2,…,X_n=x_n)$は確率変数$X_i$とその実現値$x_i$の対応と同様に考えることができる。よって、推定量は確率変数である一方で、推定値は観測値に基づく具体的な値を示すことも合わせて抑えておくと良い。

・解説
vⅱ)で取り扱ったように、確率変数$X$とその実現値$x$に関連して、推定量$T=T(X_1,X_2,…,X_n)$と推定値$t=T(X_1=x_1,X_2=x_2,…,X_n=x_n)$に関して抑えておくことで、用法に関して理解がしやすいのではないかと思います。

ベイズの定理

・問題
i) 事象Aと事象Bに関して、$P(A \cap B)=P(A|B)P(B)$であることを解釈せよ。
ⅱ) $P(A|B)P(B)=P(B|A)P(A)$が成立することを導出し、下記のベイズの定理の式を導出せよ。
$$
\begin{align}
P(A|B) = \frac{P(B|A)P(A)}{P(B)} \quad (1)
\end{align}
$$
ⅲ) $P(A)=0.5, P(B)=0.3, P(A \cap B)=0.1$のとき、$P(A|B), P(B|A)$を求め、$(1)$式が成立することを確認せよ。

・解答
i)
「$A$と$B$の両方が起こる確率」は$「B$が起こる確率」と「$B$が起こった上で$A$が起こる確率」を掛け合わせることで計算できると解釈できる。

ⅱ)
i)に基づいて考えることで、$P(A \cap B)=P(A|B)P(B)$かつ$P(A \cap B)=P(B|A)P(A)$が成立する。よって、$P(A|B)P(B)=P(B|A)P(A)$が成立する。また、両辺を$P(B)$で割ることにより、ベイズの定理を表す$(1)$式の導出を行うことができる。

ⅲ)
$P(A|B), P(B|A)$は下記のように計算することができる。
$$
\large
\begin{align}
P(A|B) &= \frac{P(A \cap B)}{P(B)} \\
&= \frac{0.1}{0.3} \\
&= \frac{1}{3} \\
P(B|A) &= \frac{P(A \cap B)}{P(A)} \\
&= \frac{0.1}{0.5} \\
&= \frac{1}{5}
\end{align}
$$

ここで$\displaystyle \frac{P(B|A)P(A)}{P(B)}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{P(B|A)P(A)}{P(B)} &= \frac{\frac{1}{5} \times 0.5}{0.3} \\
&= \frac{0.1}{0.3} \\
&= \frac{1}{3} = P(A|B)
\end{align}
$$
上記より、$(1)$式で表されたベイズの定理が成立していることが確認できる。

・解説
ベイズの定理はベイズ推定などにも出てくるなど統計学の主要なトピックなので、抑えておくと良いと思います。

スターリングの公式の理解

・問題
$n$が大きい際に$n!$の近似を行う手法の一つに下記で表したスターリングの公式がある。
$$
\large
\begin{align}
\log_{e} n! \simeq \left( n + \frac{1}{2} \right) \log_{e} n – n + \frac{1}{2} \log_{e} 2 \pi
\end{align}
$$
上記を元に以下の問いに答えよ。
i) $3!$、$5!$、$7!$をそれぞれ計算せよ。
ⅱ) $10!$を計算せよ。
ⅲ) スターリングの公式を用いて$\log_{e} 10!$の近似値を計算せよ。
iv)とⅲ)の結果について解釈を述べよ。
v) スターリングの公式を用いて$\log_{e} 20!$の近似値を計算せよ。

・解答
i)
それぞれ下記のように計算できる。
$$
\large
\begin{align}
3! &= 3 \cdot 2 \cdot 1 \\
&= 6 \\
5! &= 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \\
&= 120 \\
7! &= 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \\
&= 5040
\end{align}
$$

ⅱ)
計算結果は下記のようになる。
$$
\large
\begin{align}
10! &= 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \\
&= 3628800
\end{align}
$$

確率変数の理解

参考

・基礎統計学Ⅰ 統計学入門(東京大学出版会)

統計学入門 (基礎統計学Ⅰ)

3,080円(11/11 04:09時点)

Amazon

・第4章解答
https://www.hello-statisticians.com/explain-books-cat/toukeigakunyuumon-akahon/ch4_practice-html.html

下記などで取り扱った、回帰の重要な式に関する問題演習を通した理解ができるように問題・解答・解説をそれぞれ作成しました。
https://www.hello-statisticians.com/explain-terms-cat/regression1.html

基本問題

回帰分析の問題設定と最小二乗法

・問題
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} 1 \\ 1 \end{array}\right), \left(\begin{array}{c} 2 \\ 2 \end{array}\right)
\end{align}
$$
上記のサンプルが観測されたとき、以下の問いに答えよ。

i) 二点を通る直線の式を求めよ。
ⅱ) さらに観測を続けた際に$\displaystyle \left(\begin{array}{c} 3 \\ 3 \end{array}\right)$が得られたとする。i)で求めた直線はこの点を通るかどうかについて判定せよ。
ⅲ) 下記のようなサンプルが得られた際に、$y=ax+b$で近似することを考える。
$$
\begin{align}
\left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} 1 \\ 1 \end{array}\right), \left(\begin{array}{c} 2 \\ 2 \end{array}\right), \left(\begin{array}{c} 3 \\ 2 \end{array}\right), \left(\begin{array}{c} 2 \\ 3 \end{array}\right), \left(\begin{array}{c} 3 \\ 5 \end{array}\right)
\end{align}
$$
最小二乗法で近似するすると考えた際の二乗和$S(a,b)$を求めよ。ただし、サンプル$\displaystyle \left(\begin{array}{c} x_1 \\ y_1 \end{array}\right), …, \left(\begin{array}{c} x_n \\ y_n \end{array}\right)$に対して、二乗和$S(a,b)$は下記のように計算できるものとし、二乗それぞれの展開は行わなくて良いものとする。
$$
\large
\begin{align}
S(a, b) = \sum_{i=1}^{n} (y_i-ax_i-b)^2
\end{align}
$$
iv) ⅲ)の式に$S(a,b)=S(1,0), S(1,1), S(2,0)$を代入し、それぞれ値を計算せよ。
v) $S(a,b)$のaとbに関する偏微分を計算し、$S(a,b)$を最小にする$a$と$b$の値を求めよ。

・解答
i)
$y=ax+b$に$\displaystyle \left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} 1 \\ 1 \end{array}\right), \left(\begin{array}{c} 2 \\ 2 \end{array}\right)$を代入し、$a$と$b$の連立方程式を作成すると下記のようになる。
$$
\large
\begin{align}
1 = a + b \\
2 = 2a + b
\end{align}
$$
上記を解くことで、$a=1$、$b=0$を得ることができる。よって求める直線の式は$y=x$となる。

ⅱ)
$y=x$に$x=3$、$y=3$を代入しても成立するので、$y=x$は$\displaystyle \left(\begin{array}{c} 3 \\ 3 \end{array}\right)$を通る。

ⅲ)
二乗和$S(a,b)$は下記のように求めることができる。
$$
\begin{align}
S(a, b) &= \sum_{i=1}^{n} (y_i-ax_i-b)^2 \\
&= (1-a-b)^2 + (2-2a-b)^2 + (2-3a-b)^2 + (3-2a-b)^2 + (5-3a-b)^2
\end{align}
$$

iv)
$S(a,b)=S(1,0), S(1,1), S(2,0)$の値はそれぞれ下記のようになる。
$$
\begin{align}
S(1, 0) &= (1-1-0)^2 + (2-2-0)^2 + (2-3-0)^2 + (3-2-0)^2 + (5-3-0)^2 \\
&= 0^2 + 0^2 + (-1)^2 + 1^2 + 2^2 \\
&= 6
\end{align}
$$
$$
\begin{align}
S(1, 1) &= (1-1-1)^2 + (2-2-1)^2 + (2-3-1)^2 + (3-2-1)^2 + (5-3-1)^2 \\
&= (-1)^2 + (-1)^2 + (-2)^2 + 0^2 + 1^2 \\
&= 7
\end{align}
$$
$$
\begin{align}
S(2, 0) &= (1-2-0)^2 + (2 – 2 \cdot 2 – 0)^2 + (2 – 3 \cdot 2 – 0)^2 + (3 – 2 \cdot 2 – 0)^2 + (5 – 3 \cdot 2 – 0)^2 \\
&= (-1)^2 + (-2)^2 + (-4)^2 + (-1)^2 + (-1)^2 \\
&= 23
\end{align}
$$

v)
$$
\begin{align}
S(a, b) &= \sum_{i=1}^{n} (y_i-ax_i-b)^2 \\
&= (1-a-b)^2 + (2-2a-b)^2 + (2-3a-b)^2 + (3-2a-b)^2 + (5-3a-b)^2
\end{align}
$$
上記の二乗和$S(a,b)$を$a$と$b$に関して偏微分を行う。
$$
\begin{align}
\frac{\partial S(a, b)}{\partial a} &= -2(1-a-b) – 2(2-2a-b) \cdot 2 – 2(2-3a-b) \cdot 3 – (3-2a-b) \cdot 2 + -2(5-3a-b) \cdot 3 \\
&= 32-27a-11b
\end{align}
$$
$$
\begin{align}
\frac{\partial S(a, b)}{\partial b} &= -2(1-a-b) – 2(2-2a-b) – 2(2-3a-b) – (3-2a-b) + -2(5-3a-b) \\
&= 13-11a-5b
\end{align}
$$
ここで$32-27a-11b=0$と$13-11a-5b=0$が同時に成り立つ$a$と$b$はそれぞれ、$\displaystyle a = \frac{17}{14}, b = -\frac{1}{14}$となる。

・解説
v)で求めた最適解がiv)で求めた中で$S(a,b)$が一番小さかった$a=1, b=0$に近い値であることは着目しておくと良いと思います。

回帰式の公式の導出とその理解

・問題
$$
\begin{align}
S(a, b) = \sum_{i=1}^{n} (y_i-ax_i-b)^2
\end{align}
$$
$y=ax+b$のように回帰式を求めるにあたっては上記のような二乗誤差を最小にする$a, b$を選ぶというのが一般的な手法であり、最小二乗法と呼ばれる。この際に$S(a,b)$を最小にする$a, b$を求めるにあたって、先に各サンプルの代入を行ったのちに計算する方法もあるが、計算が多くなることから先に$a,b$をサンプルの式で求めたのちにそれぞれ値を代入するという方法の方が用いられることが多い。
以下、$a,b$の導出に関する下記の問題に答えよ。
i) $S(a,b)$を$a, b$についてそれぞれ偏微分せよ。
ⅱ) $S(a,b)$の最小点ではi)で求めた$2$式が$0$に一致すると考え、作成する方程式を正規方程式(normal equation)という。aとbの連立方程式の形式でこの正規方程式を表せ。ただし、$x_i$と$y_i$の平均をそれぞれ$\bar{x}$、$\bar{y}$とし、それらを表記になるべく用いるものとする。
ⅲ) ⅱ)で作成した連立方程式を$a$と$b$について解け。
iv) ⅲ)で導出した式を元に、$y=x$で近似される時のサンプルを作成せよ。ただし、全てのサンプルが$y=x$上の点ではあってはならないとする。
v) iv)で求めた点を元に$S(a,b)$の関数を計算し、$S(a,b)$が最小となる際に$a=1, b=0$に一致することを確かめよ。

・解答
i)
合成関数の微分の考え方を用いて、偏微分はそれぞれ下記のようになる。
$$
\large
\begin{align}
\frac{\partial S(a, b)}{\partial a} &= -2 \sum_{i=1}^{n} (y_i-ax_i-b)x_i \\
\frac{\partial S(a, b)}{\partial b} &= -2 \sum_{i=1}^{n} (y_i-ax_i-b)
\end{align}
$$

ⅱ)
i)で求めた$\displaystyle \frac{\partial S(a, b)}{\partial a}, \frac{\partial S(a, b)}{\partial b}$をそれぞれ$\displaystyle \sum_{i=1}^{n}$に着目して整理する。$\displaystyle \frac{\partial S(a, b)}{\partial a}$より確認する。
$$
\large
\begin{align}
\frac{\partial S(a, b)}{\partial a} &= -2 \sum_{i=1}^{n} (y_i-ax_i-b)x_i \\
&= -2 \sum_{i=1}^{n} (x_iy_i-ax_i^2-bx_i) \\
&= -2 \left( \sum_{i=1}^{n} x_iy_i – a \sum_{i=1}^{n} x_i^2 – b \sum_{i=1}^{n} x_i \right) \\
&= -2 \left( \sum_{i=1}^{n} x_iy_i – a \sum_{i=1}^{n} x_i^2 – b(n \bar{x}) \right) \\
&= -2 \left( \sum_{i=1}^{n} x_iy_i – a \sum_{i=1}^{n} x_i^2 – nb \bar{x} \right)
\end{align}
$$
上記が$0$となることから、さらに式を整理する。
$$
\large
\begin{align}
-2 \left( \sum_{i=1}^{n} x_iy_i – a \sum_{i=1}^{n} x_i^2 – nb \bar{x} \right) &= 0 \\
\sum_{i=1}^{n} x_iy_i – a \sum_{i=1}^{n} x_i^2 – nb \bar{x} &= 0 \\
\left( \sum_{i=1}^{n} x_i^2 \right) a + n \bar{x} b &= \sum_{i=1}^{n} x_iy_i
\end{align}
$$

次に$\displaystyle \frac{\partial S(a, b)}{\partial b}$について確認する。
$$
\large
\begin{align}
\frac{\partial S(a, b)}{\partial b} &= -2 \sum_{i=1}^{n} (y_i-ax_i-b) \\
&= -2 \left( \sum_{i=1}^{n} y_i – a \sum_{i=1}^{n} x_i – nb \right) \\
&= -2 (n \bar{y} – na \bar{x} – nb)
\end{align}
$$
上記が$0$となることから、さらに式を整理する。
$$
\large
\begin{align}
-2 (n \bar{y} – na \bar{x} – nb) &= 0 \\
n \bar{y} – na \bar{x} – nb &= 0 \\
(n \bar{x}) a + nb &= n \bar{y}
\end{align}
$$

ここまでの導出により、正規方程式は下記の連立方程式で表すことができる。
$$
\large
\begin{align}
& \left( \sum_{i=1}^{n} x_i^2 \right) a + (n \bar{x}) b = \sum_{i=1}^{n} x_iy_i \\
& (n \bar{x}) a + nb = n \bar{y}
\end{align}
$$

ⅲ)
ⅱ)の結果の$2$つ目の式に$\bar{x}$をかけると下記のようになる。
$$
\large
\begin{align}
\left( \sum_{i=1}^{n} x_i^2 \right) a + (n \bar{x}) b &= \sum_{i=1}^{n} x_iy_i \\
(n \bar{x}^2) a + (n \bar{x}) b &= n \bar{x} \bar{y}
\end{align}
$$
上記の$2$式の差を取ると、$b$に関する項を消去することができ、下記のように$a$の値を求めることができる。
$$
\begin{align}
\left( \sum_{i=1}^{n} x_i^2 – n \bar{x}^2 \right) a &= \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y} \\
a &= \frac{\displaystyle \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y}}{\displaystyle \sum_{i=1}^{n} x_i^2 – n \bar{x}^2}
\end{align}
$$

また、aがわかれば、$n \bar{x} a + nb = n \bar{y}$より、下記のようにbを求めることができる。
$$
\large
\begin{align}
n \bar{x} a + nb &= n \bar{y} \\
\bar{x} a + b &= \bar{y} \\
b &= \bar{y} – \bar{x} a
\end{align}
$$

iv)
$$
\large
\begin{align}
a &= \frac{\displaystyle \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y}}{\displaystyle \sum_{i=1}^{n} x_i^2 – n \bar{x}^2} = 1 \\
b &= \bar{y} – \bar{x} a = 0
\end{align}
$$
上記を整理すると下記のような式が導出できる。
$$
\large
\begin{align}
\sum_{i=1}^{n}x_i(y_i-x_i) &= 0 \\
\bar{y} &= \bar{x}
\end{align}
$$
上記が成立するように$x_i, y_i$を考えると、下記がサンプル群の一例となる。
$$
\large
\begin{align}
\left(\begin{array}{c} 1 \\ 1 \end{array}\right), \left(\begin{array}{c} 2 \\ 2 \end{array}\right), \left(\begin{array}{c} 0 \\ 1 \end{array}\right), \left(\begin{array}{c} 0 \\ -1 \end{array}\right), \left(\begin{array}{c} 0 \\ 0 \end{array}\right)
\end{align}
$$

v)
$S(a,b)$を計算すると下記のようになる。
$$
\large
\begin{align}
S(a, b) &= \sum_{i=1}^{n} (y_i-ax_i-b)^2 \\
&= (1-a-b)^2 + (2-2a-b)^2 + (1-b)^2 + (-1-b)^2 + b^2 \\
&= 5a^2 + 6ab + 3b^2 – 10a – 6b + 7
\end{align}
$$
上記の$a, b$に関する偏微分は下記のようになる。
$$
\large
\begin{align}
\frac{\partial S(a, b)}{\partial a} &= 10a + 6b – 10 = 0 \\
\frac{\partial S(a, b)}{\partial b} &= 6a + 6b – 6 = 0
\end{align}
$$
上記を解くことで$a=1, b=0$となり、回帰式は$y=x$となる。

・解説
ⅲ)の導出結果が公式となるので、これは抑えておくと良いです。係数の$a$の値は$x$と$y$の共分散を$x$の分散で割った値と見ることもできることも知っておくと良いと思います。

発展問題

最小二乗法の導出結果と相関係数

・問題
サンプル$(x_1,y_1), …, (x_n,y_n)$が観測された時、これを$y_i=ax_i+b$で近似することを考える。この時、最小二乗法を用いることで、$a, b$は下記のように計算することができる。
$$
\large
\begin{align}
a &= \frac{\displaystyle \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y}}{\displaystyle \sum_{i=1}^{n} x_i^2 – n \bar{x}^2} \\
b &= \bar{y} – \bar{x} a
\end{align}
$$
上記において、$\bar{x},\bar{y}$はそれぞれ$x_i, y_i$の平均であるとする。このように表した$a, b$について下記の問いに答えよ。
i) $x_i$の不偏標本分散を$s_x^2$と表記するとした時、$s_x^2$について下記が成立することを示せ。
$$
\large
\begin{align}
s_x^2 = \frac{1}{n-1} \left( \sum_{i=1}^{n} x_i^2 – n \bar{x}^2 \right)
\end{align}
$$
ⅱ) $(x_i,y_i)$の不偏標本共分散を$s_{xy}$と表記するとした時、$s_{xy}$について下記が成立することを示せ。
$$
\large
\begin{align}
s_{xy} = \frac{1}{n-1} \left( \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y} \right)
\end{align}
$$
ⅲ) 回帰式の係数$a$は下記のように表すことができることを示せ。
$$
\large
\begin{align}
a &= \frac{s_{xy}}{s_x^2}
\end{align}
$$
iv) 相関係数の式は下記のように表すことができる。
$$
\large
\begin{align}
r &= \frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})^2}}
\end{align}
$$
$x_i$の不偏標本分散を$s_x^2$、$y_i$の不偏標本分散を$s_y^2$、$(x_i,y_i)$の不偏標本共分散を$s_{xy}$とするとき、相関係数$r$を$s_x^2$、$s_y^2$、$s_{xy}$を用いて表せ。
v) 相関係数$r$と回帰式の係数$a$の関係式を書け。ただし、$r$、$a$、$s_x^2$、$s_y^2$、$s_{xy}$以外の文字は用いてはいけないものとする。

・解答
i)
確率変数$X$の期待値を$E[X]$、分散を$V[X]$とする。このとき、$s_x^2$は下記のように導出できる。
$$
\large
\begin{align}
s_x^2 &= \frac{n}{n-1} V[X] \\
&= \frac{n}{n-1} (E[X^2]-E[X]^2) \\
&= \frac{1}{n-1} (nE[X^2] – nE[X]^2) \\
&= \frac{1}{n-1} \left( \sum_{i=1}^{n}x_i^2 – n \bar{x}^2 \right)
\end{align}
$$
途中式で$V[X]=E[X^2]-E[X]^2$が成立することを利用した。

ⅱ)
確率変数$X$の期待値を$E[X]$、$Y$の期待値を$E[Y]$、$X$と$Y$の共分散を$Cov(X,Y)$とする。このとき、$s_{xy}$は下記のように導出できる。
$$
\large
\begin{align}
s_{xy} &= \frac{n}{n-1} Cov(X,Y) \\
&= \frac{n}{n-1} (E[XY] – E[X]E[Y]) \\
&= \frac{1}{n-1} (nE[XY] – nE[X]E[Y]) \\
&= \frac{1}{n-1} \left( \sum_{i=1}^{n}x_iy_i – n \bar{x}\bar{y} \right)
\end{align}
$$
途中式で$Cov(X,Y) = E[XY] – E[X]E[Y]$が成立することを利用した。

ⅲ)
i)の導出結果をⅱ)で割ることで、係数$a$の式を導出することができる。
$$
\large
\begin{align}
\frac{s_{xy}}{s_x^2} &= \frac{\displaystyle \sum_{i=1}^{n} x_iy_i – n \bar{x} \bar{y}}{\displaystyle \sum_{i=1}^{n} x_i^2 – n \bar{x}^2} \\
&= a
\end{align}
$$

iv)
i)〜ⅲ)と同様に考えて、下記が導出できる。
$$
\large
\begin{align}
r &= \frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})^2}} \\
&= \frac{s_{xy}}{\sqrt{s_x^2}\sqrt{s_y^2}}
\end{align}
$$

v)
ⅲ)の式より$s_{xy} = s_{x}^2 a$となるので、これをiv)の式に代入する。
$$
\large
\begin{align}
r &= \frac{s_{xy}}{\sqrt{s_x^2}\sqrt{s_y^2}} \\
&= \frac{s_{x}^2}{\sqrt{s_x^2}\sqrt{s_y^2}} a \\
&= \sqrt{\frac{s_{x}^2}{s_{y}^2}} a
\end{align}
$$

回帰の効果と決定係数

・問題
サンプル$(x_i,y_i)$に関して$\hat{y}_i=ax_i+b$で近似を行った際に、最小二乗法を用いてaを求めると下記のようになる。
$$
\large
\begin{align}
a &= \frac{s_{xy}}{s_x^2} \\
&= \frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2} \qquad (1)
\end{align}
$$
このとき、以下にそれぞれ答えよ。
i) $(1)$式より下記の式を導出せよ。
$$
\large
\begin{align}
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – \bar{y} – a(x_i-\bar{x}) ) = 0
\end{align}
$$
ⅱ) i)で導出した式において、$\bar{y}=a\bar{x}+b$が成立することを利用して、下記の式を導出せよ。
$$
\large
\begin{align}
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – (ax_i+b) ) = 0
\end{align}
$$
ⅲ) ⅱ)で導出した式において、$\hat{y}_i-\bar{y} = a(x_i-\bar{x})$や$\hat{y}_i=ax_i+b$が成立することを利用して、下記の式を導出せよ。
$$
\large
\begin{align}
\sum_{i=1}^{n} (\hat{y}_i-\bar{y})(y_i-\hat{y_i}) = 0
\end{align}
$$
iv) ⅲ)で導出した式などを用いて下記が成立することを示せ。
$$
\large
\begin{align}
\sum_{i=1}^{n} (y_i-\bar{y})^2 = \sum_{i=1}^{n} (y_i-\hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2
\end{align}
$$
v) iv)の式の解釈について述べよ。

・解答
i)
下記のように導出することができる。
$$
\large
\begin{align}
\frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2} &= a \\
\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) &= a \sum_{i=1}^{n}(x_i-\bar{x})^2 \\
\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) &= \sum_{i=1}^{n} a(x_i-\bar{x})^2 \\
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – \bar{y} – a(x_i-\bar{x}) ) &= 0
\end{align}
$$

ⅱ)
$\bar{y}=a\bar{x}+b$を用いることで下記のように導出することができる。
$$
\large
\begin{align}
\large
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – \bar{y} – a(x_i-\bar{x}) ) &= 0 \\
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – (a\bar{x}+b) – a(x_i-\bar{x}) ) &= 0 \\
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – (ax_i+b) ) &= 0
\end{align}
$$

ⅲ)
$\hat{y}_i-\bar{y} = a(x_i-\bar{x})$と$\hat{y}_i=ax_i+b$が成立することを用いることで、下記のように導出することができる。
$$
\large
\begin{align}
\sum_{i=1}^{n}(x_i-\bar{x})( y_i – (ax_i+b) ) &= 0 \\
\sum_{i=1}^{n} \frac{(y_i-\bar{y})}{a}( y_i – \hat{y_i} ) &= 0 \\
\sum_{i=1}^{n} (\hat{y}_i-\bar{y})(y_i-\hat{y}_i) &= 0
\end{align}
$$

iv)
ⅲ)で導出した$\displaystyle \sum_{i=1}^{n} (\hat{y}_i-\bar{y})(y_i-\hat{y}_i) = 0$を元に下記のように導出することができる。
$$
\large
\begin{align}
\sum_{i=1}^{n} (y_i-\bar{y})^2 &= \sum_{i=1}^{n} (y_i-\hat{y}_i+\hat{y}_i-\bar{y})^2 \\
&= \sum_{i=1}^{n} ((y_i-\hat{y}_i)+(\hat{y}_i-\bar{y}))^2 \\
&= \sum_{i=1}^{n} ((y_i-\hat{y}_i)^2+(\hat{y}_i-\bar{y})^2+2(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})) \\
&= \sum_{i=1}^{n} (y_i-\hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2 + 2\sum_{i=1}^{n} (y_i-\hat{y}_i)(\hat{y}_i-\bar{y})) \\
&= \sum_{i=1}^{n} (y_i-\hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2
\end{align}
$$

v)
iv)で導出した$\displaystyle \sum_{i=1}^{n} (y_i-\bar{y})^2 = \sum_{i=1}^{n} (y_i-\hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2$は回帰の効果を表していると考えることができる。左辺は「各サンプル$y_i$の平均$\bar{y}$からの散らばりの度合い」を表しており、右辺は「予測値$\hat{y}_i$と実測$y_i$の差」と「予測値$\hat{y}_i$と平均$\bar{y}$の差」の二つに式を分解している。
このうち「予測値$\hat{y}_i$と平均$\bar{y}$の差」が回帰の効果を表しており、この値を左辺の「各サンプル$y_i$の平均$\bar{y}$からの散らばりの度合い」で割ることで、下記のように決定係数$\eta^2$を定義し、決定係数について考えることも多い。
$$
\large
\begin{align}
\eta^2 = \frac{\displaystyle \sum_{i=1}^{n} (y_i-\hat{y}_i)^2}{\displaystyle \sum_{i=1}^{n} (y_i-\bar{y})^2}
\end{align}
$$

決定係数と相関係数

・問題
サンプル$(x_i,y_i)$に関して$\hat{y}_i=ax_i+b$で近似を行った際の回帰の効果を考えると下記のようになる。
$$
\begin{align}
\sum_{i=1}^{n} (y_i-\bar{y})^2 = \sum_{i=1}^{n} (y_i-\hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2
\end{align}
$$
また、独立変数$x$が従属変数$y$を決定する度合いを表す決定係数$\eta^2$を下記のように定義する。
$$
\large
\begin{align}
\eta^2 = \frac{\displaystyle \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2}{\displaystyle \sum_{i=1}^{n} (y_i-\bar{y})^2}
\end{align}
$$
上記の式を元に以下の問題に答えよ。
i) $\hat{y}_i-\bar{y}=a(x_i-\bar{x})$、$\displaystyle a=r \sqrt{\frac{s_y^2}{s_x^2}}$を活用し、下記を導出せよ。
$$
\begin{align}
\sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2 = r^2 \sum_{i=1}^{n} (y_i-\bar{y})^2
\end{align}
$$
ⅱ) $\eta^2=r^2$を導出せよ。
ⅲ) ⅱ)で導出した$\eta^2=r^2$の解釈を述べよ。
iv) $r=1$となるサンプルの例を挙げよ。ただしサンプル数は$n=5$とする。
v) iv)で作成したサンプルの決定係数$\eta^2$を計算し、$\eta^2=1$が成り立つことを確認せよ。

・解答
i)
$$
\large
\begin{align}
\sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2 &= \sum_{i=1}^{n} a^2(x_i-\bar{x})^2 \\
&= r^2 \frac{s_y^2}{s_x^2} \cdot \sum_{i=1}^{n} (x_i-\bar{x})^2 \\
&= r^2 \frac{s_y^2}{s_x^2} \cdot s_x^2 \\
&= r^2 s_y^2 \\
&= r^2 \sum_{i=1}^{n} (y_i-\bar{y})^2
\end{align}
$$

ⅱ)
i)で導出した式を$\eta^2$の定義式に代入すればよい。
$$
\large
\begin{align}
\eta^2 &= \frac{\displaystyle \sum_{i=1}^{n} (\hat{y}_i-\bar{y})^2}{\displaystyle \sum_{i=1}^{n} (y_i-\bar{y})^2} \\
&= \frac{\displaystyle r^2 \sum_{i=1}^{n} (y_i-\bar{y})^2}{\displaystyle \sum_{i=1}^{n} (y_i-\bar{y})^2} \\
&= r^2
\end{align}
$$

ⅲ)
決定係数$\eta^2$は回帰を用いた予測の効果についての度合いを取り扱っている一方で、相関係数の$r^2$は$y$と$x$の連動の度合いを表している。ⅱ)で$\eta^2=r^2$を示したことにより、最小二乗法によって予測した場合の予測の効果は$x$と$y$の連動の度合いに一致することがわかったと考えると良い。

iv)
下記のようにサンプルを考えると、相関係数$r=1$となる。
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} 1 \\ 1 \end{array}\right), \left(\begin{array}{c} 2 \\ 2 \end{array}\right), \left(\begin{array}{c} 3 \\ 3 \end{array}\right), \left(\begin{array}{c} 4 \\ 4 \end{array}\right), \left(\begin{array}{c} 5 \\ 5 \end{array}\right)
\end{align}
$$

v)
iv)で作成したサンプルは全て$y=x$の点となるため、$\hat{y}_i = y_i$となるため、$\eta^2$の定義式より、$\eta^2=1$となる。

最良線型不偏推定量に関して

・問題
「基礎統計学Ⅰ 統計学入門(東京大学出版会)」の章末問題の11.2を主に参考にする。
標本$X_1, X_2$に基づく$\mu$の推定量を$aX_1+bX_2$のように考えるとする。
このとき以下の問題に答えよ。
i) 推定量$aX_1+bX_2$が不偏性を持つには$a+b=1$となる必要があることを導出せよ。

・解答
i)
推定量$aX_1+bX_2$が不偏性を持つには$E[aX_1+bX_2]=E[X_1]=E[X_2]$が成立する必要がある。これより$a+b=1$が導出できる。

参考書籍

・基礎統計学Ⅰ 統計学入門(東京大学出版会)
第$3$章と第$13$章を主に参考にしました。

統計学入門 (基礎統計学Ⅰ)

3,080円(11/11 04:09時点)

Amazon

下記などで取り扱った、多次元正規分布に関する問題演習を通した理解ができるように問題・解答・解説をそれぞれ作成しました。

・標準演習$100$選
https://www.hello-statisticians.com/practice_100

基本問題

直交行列

・問題
$$
\large
\begin{align}
\mathbf{U}\mathbf{U}^{\mathrm{T}} = \mathbf{U}^{\mathrm{T}}\mathbf{U} = \mathbf{I}
\end{align}
$$
上記が成立する行列$\mathbf{U}$を直交行列という。直交行列について下記の問題に答えよ。
i) 直交する2つの大きさ1の2次元のベクトルの例を一つあげよ。
ⅱ) i)で作成した2つの2次元ベクトルを用いて直交行列$\mathbf{U}$を作成せよ。
ⅲ) ⅱ)で作成した直交行列に対して、$\mathbf{U}\mathbf{U}^{\mathrm{T}}$、$\mathbf{U}^{\mathrm{T}}\mathbf{U}$、$\mathbf{U}^{-1}$を計算せよ。

・解答
i)
いくつか例がある方が良いので、以下に3例あげる。
$$
\large
\begin{align}
& \left(\begin{array}{c} 1 \\ 0 \end{array}\right), \left(\begin{array}{c} 0 \\ 1 \end{array}\right) \\
& \frac{1}{\sqrt{2}}\left(\begin{array}{c} 1 \\ 1 \end{array}\right), \frac{1}{\sqrt{2}}\left(\begin{array}{c} -1 \\ 1 \end{array}\right) \\
& \frac{1}{\sqrt{5}}\left(\begin{array}{c} 2 \\ 1 \end{array}\right), \frac{1}{\sqrt{5}}\left(\begin{array}{c} -1 \\ 2 \end{array}\right)
\end{align}
$$

ⅱ)
$$
\large
\begin{align}
\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1 \\ 1 \end{array}\right), \frac{1}{\sqrt{2}}\left(\begin{array}{c} -1 \\ 1 \end{array}\right)
\end{align}
$$
上記を用いて、下記のような直交行列$\mathbf{U}$を作成することができる。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right)
\end{align}
$$

ⅲ)
$$
\large
\begin{align}
\mathbf{U}\mathbf{U}^{\mathrm{T}} &= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right)\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \cdot (-\frac{1}{\sqrt{2}}) + \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + (-\frac{1}{\sqrt{2}}) \cdot \frac{1}{\sqrt{2}} & (-\frac{1}{\sqrt{2}}) \cdot (-\frac{1}{\sqrt{2}}) + \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align}
$$

$$
\large
\begin{align}
\mathbf{U}^{\mathrm{T}}\mathbf{U} &= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right)\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + (-\frac{1}{\sqrt{2}}) \cdot (-\frac{1}{\sqrt{2}}) & \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + (-\frac{1}{\sqrt{2}}) \cdot \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \cdot (-\frac{1}{\sqrt{2}}) & \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align}
$$

$$
\large
\begin{align}
\mathbf{U}^{-1} &= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right)^{-1} \\
&= \frac{1}{(1/\sqrt{2} \cdot 1/\sqrt{2}) – (1/\sqrt{2} \cdot (-1/\sqrt{2}))} \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \left(\begin{array}{cc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right) \\
&= \mathbf{U}^{\mathrm{T}}
\end{align}
$$

・解説
$D$次元の行列の大きさ1の固有ベクトルを$\mathbf{u}_1, \mathbf{u}_2, …, \mathbf{u}_D$としたとき、下記のように並べることで直交行列を作ることができます。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{c} \mathbf{u}_1 \\ \mathbf{u}_2 \\ … \\ \mathbf{u}_D \end{array} \right)
\end{align}
$$
このことは分散共分散行列を元にした議論を行う際に色々と出てくるので、必ず抑えておくと良いと思います。

基底の変換

・問題
下記のように$\mathbf{e}_1, \mathbf{e}_2, \mathbf{a}_1, \mathbf{a}_2$を定義する。
$$
\large
\begin{align}
\mathbf{e}_1 = \left(\begin{array}{c} 1 \\ 0 \end{array} \right), \quad \mathbf{e}_2 = \left(\begin{array}{c} 0 \\ 1 \end{array} \right), \quad \mathbf{a}_1 = \left(\begin{array}{c} 2 \\ 1 \end{array} \right), \quad \mathbf{a}_2 = \left(\begin{array}{c} 1 \\ 2 \end{array} \right)
\end{align}
$$
このとき下記の問いに答えよ。このとき下記の問いに答えよ。
i) $\mathbf{a}_1, \mathbf{a}_2$が線型独立であることを示せ。
ⅱ) $\mathbf{a}_1, \mathbf{a}_2$をそれぞれ$\mathbf{e}_1, \mathbf{e}_2$を用いて表せ。
ⅲ) $\mathbf{t} = x\mathbf{e}_1 + y\mathbf{e}_2 = X\mathbf{a}_1 + Y\mathbf{a}_2$のように表せるとき、$\displaystyle \left(\begin{array}{c} x \\ y \end{array} \right) = \mathbf{A}\left(\begin{array}{c} X \\ Y \end{array} \right)$が成立する行列$\mathbf{A}$を求めよ。

・解答
i)
$$
\large
\begin{align}
s\mathbf{a}_1 + t\mathbf{a}_2 = \left(\begin{array}{c} 0 \\ 0 \end{array} \right)
\end{align}
$$
$\mathbf{a}_1, \mathbf{a}_2$が線型独立であることを示すには、上記が成立するとき$s=t=0$になることを示せば良い。
$$
\large
\begin{align}
s\mathbf{a}_1 + t\mathbf{a}_2 &= s\left(\begin{array}{c} 2 \\ 1 \end{array} \right) + t\left(\begin{array}{c} 1 \\ 2 \end{array} \right) \\
&= \left(\begin{array}{c} 2s + t \\ s + 2t \end{array} \right)
\end{align}
$$
$2s+t=0$と$s+2t=0$より$s=t=0$が導出できるため、$\mathbf{a}_1, \mathbf{a}_2$は線型独立である。

ⅱ)
$$
\large
\begin{align}
\mathbf{a}_1 &= \left(\begin{array}{c} 2 \\ 1 \end{array} \right) \\
&= \left(\begin{array}{c} 2 \\ 0 \end{array} \right) + \left(\begin{array}{c} 0 \\ 1 \end{array} \right) \\
&= 2\left(\begin{array}{c} 1 \\ 0 \end{array} \right) + \left(\begin{array}{c} 0 \\ 1 \end{array} \right) \\
&= 2\mathbf{e}_1 + \mathbf{e}_2 \\
\mathbf{a}_2 &= \left(\begin{array}{c} 1 \\ 2 \end{array} \right) \\
&= \left(\begin{array}{c} 1 \\ 0 \end{array} \right) + \left(\begin{array}{c} 0 \\ 2 \end{array} \right) \\
&= \left(\begin{array}{c} 1 \\ 0 \end{array} \right) + 2\left(\begin{array}{c} 0 \\ 1 \end{array} \right) \\
&= \mathbf{e}_1 + 2\mathbf{e}_2
\end{align}
$$

ⅲ)
$X\mathbf{a}_1 + Y\mathbf{a}_2$を$\mathbf{e}_1, \mathbf{e}_2$を用いて表すと下記のようになる。
$$
\large
\begin{align}
X\mathbf{a}_1 + Y\mathbf{a}_2 &= X\left(\begin{array}{c} 2 \\ 1 \end{array} \right) + Y\left(\begin{array}{c} 1 \\ 2 \end{array} \right) \\
&= \left(\begin{array}{c} 2X+Y \\ X+2Y \end{array} \right) \\
&= (2X+Y)\mathbf{e}_1 + (X+2Y)\mathbf{e}_2 \\
\end{align}
$$
ここで$x\mathbf{e}_1 + y\mathbf{e}_2 = X\mathbf{a}_1 + Y\mathbf{a}_2$であることから、下記のように表すことができる。
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array} \right) &= \left(\begin{array}{c} 2X+Y \\ X+2Y \end{array} \right) \\
&= \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right)\left(\begin{array}{c} X \\ Y \end{array} \right)
\end{align}
$$

・解説
基底の変換は多次元正規分布の理解にあたって、分散共分散行列の固有値・固有ベクトルの変換を用いる際に出てくるので必ず抑えておく必要があります。ここで取り扱ったような基底の変換については線形代数の教科書でも出てくるのですが、あまりメインで取り扱われずに導出だけ書かれていることが多いので、より注目して取り組みやすいように演習問題を作成しました。ⅲ)で取り扱った計算については慣れていないと間違えがちなので、何度も繰り返し演習を行うことで慣れておくと良いと思います。

発展問題

分散共分散行列と固有値・固有ベクトル

・問題
$\mathbf{\Sigma}$を$2$次元の分散共分散行列とし、その固有値を$\lambda_i$、大きさ1の固有ベクトルを$\mathbf{u}_i$と考えるとする。このとき下記の問いに答えよ。
i) $\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_1$、$\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_2$をそれぞれ求めよ。
ⅱ) $\displaystyle \mathbf{u}_1 = \left(\begin{array}{c} u_{11} \\ u_{12} \end{array} \right)$、$\displaystyle \mathbf{u}_2 = \left(\begin{array}{c} u_{21} \\ u_{22} \end{array} \right)$とするとき、$\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}$、$\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$をそれぞれ求めよ。
ⅲ) $\displaystyle \mathbf{U} = \left(\begin{array}{c} \mathbf{u}_1^{\mathrm{T}} \\ \mathbf{u}_2^{\mathrm{T}} \end{array} \right) = \left(\begin{array}{cc} u_{11} & u_{12} \\ u_{21} & u_{22} \end{array} \right)$のように直交行列$\mathbf{U}$を考えるとき、$\mathbf{U}^{\mathrm{T}}\mathbf{U}$を求め、$\displaystyle \mathbf{U}^{\mathrm{T}}\mathbf{U}=\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$であることを示せ。
iⅴ) $\mathbf{\Sigma}\mathbf{u}_i = \lambda_i\mathbf{u}_i$の式より、$\mathbf{\Sigma}=\lambda_1\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\lambda_2\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$であることを示せ。
ⅴ) $\displaystyle \mathbf{\Sigma}^{-1}=\frac{1}{\lambda_1}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\frac{1}{\lambda_2}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$であることを示せ。

・解答
i)
$\mathbf{u}_1$、$\mathbf{u}_2$は大きさ1の固有ベクトルであるから、$\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_1$、$\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_2$はそれぞれ下記のようになる。
$$
\large
\begin{align}
\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_1 &= 1 \\
\mathbf{u}_1^{\mathrm{T}}\mathbf{u}_2 &= 0
\end{align}
$$

ⅱ)
それぞれ下記のように計算できる。
$$
\large
\begin{align}
\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}} &= \left(\begin{array}{c} u_{11} \\ u_{12} \end{array} \right)\left(\begin{array}{cc} u_{11} & u_{12} \end{array} \right) \\
&= \left(\begin{array}{cc} u_{11}^2 & u_{11}u_{12} \\ u_{12}u_{11} & u_{12}^2 \end{array} \right) \\
\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}} &= \left(\begin{array}{c} u_{21} \\ u_{22} \end{array} \right)\left(\begin{array}{cc} u_{21} & u_{22} \end{array} \right) \\
&= \left(\begin{array}{cc} u_{21}^2 & u_{21}u_{22} \\ u_{22}u_{21} & u_{22}^2 \end{array} \right)
\end{align}
$$

ⅲ)
下記のように計算できる。
$$
\large
\begin{align}
\mathbf{U}^{\mathrm{T}}\mathbf{U} &= \left(\begin{array}{cc} u_{11} & u_{21} \\ u_{12} & u_{22} \end{array} \right)\left(\begin{array}{cc} u_{11} & u_{12} \\ u_{21} & u_{22} \end{array} \right) \\
&= \left(\begin{array}{cc} u_{11}^2+u_{21}^2 & u_{11}u_{12}+u_{21}u_{22} \\ u_{12}u_{11}+u_{22}u_{21} & u_{12}^2+u_{22}^2 \end{array} \right)
\end{align}
$$
また、上記とⅱ)の結果を比較することによって、$\displaystyle \mathbf{U}^{\mathrm{T}}\mathbf{U}=\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$を示すことができる。

iv)
$$
\large
\begin{align}
\mathbf{\Sigma}\mathbf{u}_i = \lambda_i\mathbf{u}_i
\end{align}
$$
上記の式に対し、右から$\mathbf{u}_i^{\mathrm{T}}$をかけることを考える。
$$
\large
\begin{align}
\mathbf{\Sigma}\mathbf{u}_i &= \lambda_i\mathbf{u}_i \\
\mathbf{\Sigma}\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}} &= \lambda_i\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}}
\end{align}
$$
ここで、ⅲ)で示した$\displaystyle \mathbf{U}^{\mathrm{T}}\mathbf{U}=\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}=\mathbf{I}$に基づいて、左辺に単位行列$\mathbf{I}$を作ることを考える。

$$
\large
\begin{align}
\mathbf{\Sigma}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}} + \mathbf{\Sigma}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}} &= \lambda_1\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}} + \lambda_2\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}} \\
\mathbf{\Sigma}(\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}} + \mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}) &= \sum_{i=1}^{2} \lambda_i\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}} \\
\mathbf{\Sigma}\mathbf{U}^{\mathrm{T}}\mathbf{U} &= \sum_{i=1}^{2} \lambda_i\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}} \\
\mathbf{\Sigma}\mathbf{I} &= \sum_{i=1}^{2} \lambda_i\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}} \\
\mathbf{\Sigma} &= \sum_{i=1}^{2} \lambda_i\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}}
\end{align}
$$
上記より、$\mathbf{\Sigma}=\lambda_1\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\lambda_2\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$を示すことができた。

v)
$$
\large
\begin{align}
\mathbf{\Sigma}\mathbf{u}_i = \lambda_i\mathbf{u}_i
\end{align}
$$
上記の式に対し、左から$\mathbf{\Sigma}^{-1}$をかけると下記のようになる。
$$
\large
\begin{align}
\mathbf{\Sigma}^{-1}\mathbf{\Sigma}\mathbf{u}_i &= \mathbf{\Sigma}^{-1}\lambda_i\mathbf{u}_i \\
\mathbf{u}_i &= \lambda_i\mathbf{\Sigma}^{-1}\mathbf{u}_i \\
\frac{1}{\lambda_i}\mathbf{u}_i &= \mathbf{\Sigma}^{-1}\mathbf{u}_i
\end{align}
$$
上記において$\lambda_i$のみスカラーであるため、計算順序の入れ替えや両辺に逆数をかけることができた。以下、左辺と右辺を入れ替えて、$\mathbf{\Sigma}^{-1}$について解くことを考える。
$$
\large
\begin{align}
\frac{1}{\lambda_i}\mathbf{u}_i &= \mathbf{\Sigma}^{-1}\mathbf{u}_i \\
\mathbf{\Sigma}^{-1}\mathbf{u}_i &= \frac{1}{\lambda_i}\mathbf{u}_i \\
\mathbf{\Sigma}^{-1}\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}} &= \frac{1}{\lambda_i}\mathbf{u}_i\mathbf{u}_i^{\mathrm{T}}
\end{align}
$$
以降はiv)と同様に導出することができる。

分散共分散行列と多次元正規分布の確率密度関数

・問題
平均ベクトル$\displaystyle \mathbf{\mu}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$、分散共分散行列$\displaystyle \mathbf{\Sigma}=\left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)$の2次元正規分布を考えると確率密度関数は下記のようになる。
$$
\begin{align}
N(x|\mathbf{\mu}, \mathbf{\Sigma}) = \frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} \exp \left( -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu}) \right)
\end{align}
$$
また、上記において$\Delta^2 = (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu})$と考えるものとする。
このとき、下記の問いに答えよ。
i) 分散共分散行列$\mathbf{\Sigma}$の固有値を求めよ。
ⅱ) i)で求めたそれぞれの固有値に関して、それぞれ固有ベクトルを求めよ。
ⅲ) $\displaystyle \mathbf{\Sigma}^{-1}=\frac{1}{\lambda_1}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\frac{1}{\lambda_2}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$であることを用いて、下記を導出せよ。
$$
\begin{align}
\Delta^2 = \sum_{i=1}^{2} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i}
\end{align}
$$
iv) $\displaystyle \mathbf{x}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$、$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$、$\displaystyle \mathbf{x}=\left(\begin{array}{c} 0 \\ 2 \end{array} \right)$に関してそれぞれ$\Delta^2$の値を計算せよ。ただし簡易化のために下記のように定義した$y_i$を用いても良いとする。
$$
\begin{align}
y_i = (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i = \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})
\end{align}
$$
v) $\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$と同じ$\Delta^2$の値を持つ点$\mathbf{x}$をさらに2つあげよ。

・解答
i)
$\det(\mathbf{\Sigma}-\lambda\mathbf{I})=0$を$\lambda$について解けばよい。
$$
\large
\begin{align}
\det(\mathbf{\Sigma}-\lambda\mathbf{I}) &= (1-\lambda)^2-0.7^2 \\
&= (1-\lambda+0.7)(1-\lambda-0.7) \\
&= (1.7-\lambda)(0.3-\lambda) = 0
\end{align}
$$
上記より、分散共分散行列$\mathbf{\Sigma}$の固有値は$\lambda=1.7, 0.3$となる。

ⅱ)
$\lambda=1.7$に対応する固有ベクトルを$\mathbf{u}_1$、$\lambda=0.3$に対応する固有ベクトルを$\mathbf{u}_2$とする。$\mathbf{u}_1$は下記のようになる。
$$
\begin{align}
\mathbf{\Sigma}\mathbf{u}_1 &= 1.7\mathbf{u}_1 \\
\left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)\left(\begin{array}{c} u_{11} \\ u_{12} \end{array} \right) &= 1.7\left(\begin{array}{c} u_{11} \\ u_{12} \end{array} \right) \\
\left(\begin{array}{c} u_{11}+0.7u_{12} \\ 0.7u_{11}+u_{12} \end{array} \right) &= \left(\begin{array}{c} 1.7u_{11} \\ 1.7u_{12} \end{array} \right) \\
\left(\begin{array}{c} 0.7u_{12} \\ 0.7u_{11} \end{array} \right) &= \left(\begin{array}{c} 0.7u_{11} \\ 0.7u_{12} \end{array} \right)
\end{align}
$$
上記より、$\mathbf{u}_1$の$x$成分と$y$成分が一致する。また、$\mathbf{u}_1$の大きさが$1$であることから、$\displaystyle \mathbf{u}_1 = \left(\begin{array}{c} 1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right)$となる。

次に$\mathbf{u}_2$について計算を行う。
$$
\begin{align}
\mathbf{\Sigma}\mathbf{u}_2 &= 0.3\mathbf{u}_2 \\
\left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)\left(\begin{array}{c} u{21} \\ u_{22} \end{array} \right) &= 1.7\left(\begin{array}{c} u_{21} \\ u_{22} \end{array} \right) \\
\left(\begin{array}{c} u_{21}+0.7u_{22} \\ 0.7u_{21}+u_{22} \end{array} \right) &= \left(\begin{array}{c} 0.3u_{21} \\ 0.3u_{22} \end{array} \right) \\
\left(\begin{array}{c} 0.7u_{22} \\ 0.7u_{21} \end{array} \right) &= \left(\begin{array}{c} -0.7u_{21} \\ -0.7u_{22} \end{array} \right)
\end{align}
$$
上記と$|\mathbf{u}_2|=1$より、$\displaystyle \mathbf{u}_2 = \left(\begin{array}{c} -1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right)$が導出できる。

ⅲ)
$\displaystyle \Delta^2 = (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu})$に$\displaystyle \mathbf{\Sigma}^{-1}=\frac{1}{\lambda_1}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\frac{1}{\lambda_2}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}$を代入することで、下記のように導出できる。
$$
\begin{align}
\Delta^2 &= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu}) \\
&= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \left(\frac{1}{\lambda_1}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}+\frac{1}{\lambda_2}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}} \right) (\mathbf{x}-\mathbf{\mu}) \\
&= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \left(\frac{1}{\lambda_1}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}} \right) (\mathbf{x}-\mathbf{\mu})+(\mathbf{x}-\mathbf{\mu})^{T} \left(\frac{1}{\lambda_2}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}} \right) (\mathbf{x}-\mathbf{\mu}) \\
&= \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_1\mathbf{u}_1^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu})}{\lambda_1}+\frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_2\mathbf{u}_2^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu})}{\lambda_2} \\
&= \sum_{i=1}^{2} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i}
\end{align}
$$

iv)
$\displaystyle \mathbf{x}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$は平均ベクトル$\displaystyle \mathbf{\mu}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$と一致する。よって、$y_i$は下記のように計算できる。
$$
\begin{align}
y_i &= \mathbf{u}_i^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{i1} & u_{i2} \end{array} \right)\left(\begin{array}{c} 1-1 \\ 1-1 \end{array} \right) \\
&= \left(\begin{array}{cc} u_{i1} & u_{i2} \end{array} \right)\left(\begin{array}{c} 0 \\ 0 \end{array} \right) = 0
\end{align}
$$
よって$\Delta^2$は下記のように計算できる。
$$
\begin{align}
\Delta^2 &= \sum_{i=1}^{2} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i} \\
&= \sum_{i=1}^{2} \frac{y_i^2}{\lambda_i} \\
&= \sum_{i=1}^{2} \frac{0 \cdot 0}{\lambda_i} = 0
\end{align}
$$

$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$については$y_1$と$y_2$をそれぞれ求め、$\Delta^2$を計算する。
$$
\begin{align}
y_1 &= \mathbf{u}_1^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{11} & u_{12} \end{array} \right)\left(\begin{array}{c} 2-1 \\ 2-1 \end{array} \right) \\
&= \left(\begin{array}{cc} 1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} 1 \\ 1 \end{array} \right) \\
&= 1/\sqrt{2} \cdot 1 + 1/\sqrt{2} \cdot 1 \\
&= 2/\sqrt{2} = \sqrt{2}
\end{align}
$$
$$
\begin{align}
y_2 &= \mathbf{u}_2^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{21} & u_{22} \end{array} \right)\left(\begin{array}{c} 2-1 \\ 2-1 \end{array} \right) \\
&= \left(\begin{array}{cc} -1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} 1 \\ 1 \end{array} \right) \\
&= -1/\sqrt{2} \cdot 1 + 1/\sqrt{2} \cdot 1 \\
&= 0
\end{align}
$$
よって、$\Delta^2$は下記のように計算できる。
$$
\begin{align}
\Delta^2 &= \sum_{i=1}^{2} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i} \\
&= \sum_{i=1}^{2} \frac{y_i^2}{\lambda_i} \\
&= \frac{y_1^2}{\lambda_1} \\
&= \frac{(\sqrt{2})^2}{1.7} \\
&= \frac{2}{1.7} = 1.176…
\end{align}
$$

$\displaystyle \mathbf{x}=\left(\begin{array}{c} 0 \\ 2 \end{array} \right)$については$y_1$と$y_2$をそれぞれ求め、$\Delta^2$を計算する。
$$
\begin{align}
y_1 &= \mathbf{u}_1^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{11} & u_{12} \end{array} \right)\left(\begin{array}{c} 0-1 \\ 2-1 \end{array} \right) \\
&= \left(\begin{array}{cc} 1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} -1 \\ 1 \end{array} \right) \\
&= 1/\sqrt{2} \cdot (-1) + 1/\sqrt{2} \cdot 1 \\
&= 0
\end{align}
$$
$$
\begin{align}
y_2 &= \mathbf{u}_2^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{21} & u_{22} \end{array} \right)\left(\begin{array}{c} 0-1 \\ 2-1 \end{array} \right) \\
&= \left(\begin{array}{cc} -1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} -1 \\ 1 \end{array} \right) \\
&= -1/\sqrt{2} \cdot (-1) + 1/\sqrt{2} \cdot 1 \\
&= 2/\sqrt{2} = \sqrt{2}
\end{align}
$$
よって、$\Delta^2$は下記のように計算できる。
$$
\begin{align}
\Delta^2 &= \sum_{i=1}^{2} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i} \\
&= \sum_{i=1}^{2} \frac{y_i^2}{\lambda_i} \\
&= \frac{y_2^2}{\lambda_2} \\
&= \frac{(\sqrt{2})^2}{0.3} \\
&= \frac{2}{0.3} = 6.666…
\end{align}
$$

v)
固有ベクトルの方向にある点だと考えやすいので、$\mathbf{u}_1$と$\mathbf{u}_2$の方向でそれぞれ1つずつ考えることとする。 $\mathbf{u}_1$について考えるにあたっては、$y_1$の値だけを考えればよい。求める点を$\displaystyle \left(\begin{array}{c} a+1 \\ a+1 \end{array} \right)$とおく。
$$
\begin{align} y_1 &= \mathbf{u}_1^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{11} & u_{12} \end{array} \right)\left(\begin{array}{c} a+1-1 \\ a+1-1 \end{array} \right) \\
&= \left(\begin{array}{cc} 1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} a+1-1 \\ a+1-1 \end{array} \right) \\
&= 1/\sqrt{2} \cdot a + 1/\sqrt{2} \cdot a \\
&= 2a/\sqrt{2} = \sqrt{2}a
\end{align}
$$
$y_1^2$の値が$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$と一致することより、$y_1^2=2a^2=2$を解いて$a=1, -1$が得られる。$a=1$に対応する$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$は既出のため、$a=-1$に対応する$\displaystyle \mathbf{x}=\left(\begin{array}{c} 0 \\ 0 \end{array} \right)$が求める点の一つであると考えることができる。

次に$\mathbf{u}_2$の方向について考える。$y_1=0$のため、$y_2$の値だけを考えればよい。求める点を$\displaystyle \left(\begin{array}{c} -a+1 \\ a+1 \end{array} \right)$とおき、$y_2$について計算すると下記のようになる。
$$
\begin{align}
y_2 &= \mathbf{u}_2^{\mathrm{T}}(\mathbf{x}-\mathbf{\mu}) \\
&= \left(\begin{array}{cc} u_{21} & u_{22} \end{array} \right)\left(\begin{array}{c} -a+1-1 \\ a+1-1 \end{array} \right) \\
&= \left(\begin{array}{cc} -1/\sqrt{2} & 1/\sqrt{2} \end{array} \right)\left(\begin{array}{c} -a \\ a \end{array} \right) \\
&= -1/\sqrt{2} \cdot (-a) + 1/\sqrt{2} \cdot a \\
&= 2a/\sqrt{2} = \sqrt{2}a
\end{align}
$$
この結果を元に、$\Delta^2$の値を$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$と比較すると下記のようになる。
$$
\begin{align}
\frac{(\sqrt{2}a)^2}{0.3} &= \frac{(\sqrt{2})^2}{1.7} \\
\frac{2a^2}{0.3} &= \frac{2}{1.7} \\
a^2 &= \frac{0.3}{1.7}
\end{align}
$$
上記より、$a = \pm 0.42…$が得られる。$a=0.42$について考えると、$\displaystyle \left(\begin{array}{c} -a+1 \\ a+1 \end{array} \right) = \left(\begin{array}{c} 0.58 \\ 1.42 \end{array} \right)$が得られる。

・解説
iv)で$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$と$\displaystyle \mathbf{x}=\left(\begin{array}{c} 0 \\ 2 \end{array} \right)$はどちらも$\displaystyle \mathbf{x}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$から同じだけ離れている一方で$\Delta^2$を計算すると、大きく異なった値になったことは注意しておくと良いです。これにより2次元正規分布において相関も考慮した上で中心からのズレを定義することができると理解しておくとよいです。
また、v)の結果も同様に、$\displaystyle \mathbf{x}=\left(\begin{array}{c} 2 \\ 2 \end{array} \right)$と同じ$\Delta^2$となる点を探すにあたっては、$\mathbf{u}_1$方向よりも$\mathbf{u}_2$方向の方が$\displaystyle \mathbf{x}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$の近隣の点となることを考えると、2次元正規分布の確率密度関数について理解できて良いと思います。

多次元正規分布のサンプリング

・問題
$$
\begin{align}
03, 47, 43, 73, 86, 36, 96, 47, 36, 61, 46, 98, 63, 71, 62, 33, 26, 16, 80, 45, 60, 11, 14, 10, 95 \\
97, 74, 24, 67, 62, 42, 81, 14, 57, 20, 42, 53, 32, 37, 32, 27, 07, 36, 07, 51, 24, 51, 79, 83, 73 \\
16, 76, 62, 27, 66, 56, 50, 26, 71, 07, 32, 90, 79, 78, 53, 13, 55, 38, 58, 59, 88, 97, 54, 14, 10
\end{align}
$$
上記のような乱数表がある際に、平均ベクトル$\displaystyle \mathbf{\mu}=\left(\begin{array}{c} 1 \\ 1 \end{array} \right)$、分散共分散行列$\displaystyle \mathbf{\Sigma}=\left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)$の$2$次元正規分布に従うサンプリングを行うことを考える。乱数表はR.A.フィッシャー作成の$6$表に基づいて作成された、「基礎統計学Ⅰ 統計学入門(東京大学出版会)」の$292$ページのものを用いた。
このとき以下の問いに答えよ。
i) 最上段の乱数の$10$の位ごとに区切って度数分布表を作成せよ。
ⅱ)

それぞれの列ごとに乱数を$3$つずつ平均を計算し、i)と同様に度数分布表を作成せよ。平均の計算を行うのは大変なため、下記を用いて良いものとする。
$$
\begin{align}
&38.6, 65.6, 43.0, 55.6, 71.3, 44.6, 75.6, 29.0, 54.6, 29.3, 40.0, 80.3, 58.0, 62.0, 49.0, 24.3, 29.3, \\
&30.0, 48.3, 51.6, 57.3, 53.0, 49.0, 35.6, 59.3
\end{align}
$$
ⅲ) ⅱ)の結果はi)の結果よりも正規分布に近い分布となる。この理由を述べよ。
iv) 分散共分散行列が与えられているとき、$2$つの独立した$1$次元の正規分布に基づくサンプリングに基づいて$2$次元正規分布のサンプリングを行うにはどうすれば良いか。
v) 複数のサンプルのサンプリングを同時に行う際はどのように行列計算を行えば良いか。

・解答
ⅲ)
中心極限定理より、サンプルが多くなるにつれて標本平均は正規分布で近似できるようになるため。

https://www.hello-statisticians.com/explain-terms-cat/flow_chart_stat1.html
上記などで取り扱った、区間推定(Interval estimation)の問題演習ができるように問題・解答・解説をそれぞれ作成しました。

基本問題

母平均の推定①（母分散既知）

・問題
i) $x_1, x_2, …, x_n$が得られた際の標本平均$\bar{x}$を求めよ。
ⅱ) 中心極限定理より、標本平均$\bar{x}$は正規分布$N(\mu, \sigma^2)$に従うと考えることができるとする。この時、$\displaystyle \frac{\bar{x}-\mu}{\sigma/\sqrt{n}}$はどのような分布に従うか。
ⅲ) $\displaystyle \frac{\bar{x}-\mu}{\sigma/\sqrt{n}}$の95％両側区間を求めよ。もし具体的な値がわからなければ、ⅱ)の答えの分布の上側確率を$p$とする点を$z_{\alpha=p}$のように表して区間推定を行って良いものとする。また、$p$に対して$0 \leq p \leq 1$が成立していることとする。

・解答
i)
$\bar{x}$は下記のように計算できる。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{n}(x_1+x_2+…+x_n) \\
&= \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align}
$$

ⅱ)
平均との差を標準偏差で割っていることから、標準化を行ったと考えることができる。よって、標準正規分布$N(0, 1)$に従うと考えられる。

ⅲ)
95％両側区間は下記のように求めることができる。
$$
\large
\begin{align}
z_{\alpha=0.975} \leq &\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \leq z_{\alpha=0.025} \\
z_{\alpha=0.975}\frac{\sigma}{\sqrt{n}} \leq &\bar{x}-\mu \leq z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}} \\
-z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}} \leq &\mu-\bar{x} \leq -z_{\alpha=0.975}\frac{\sigma}{\sqrt{n}} \\
-z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}} \leq &\mu-\bar{x} \leq z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}} \\
\bar{x} – z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}} \leq &\mu \leq \bar{x} + z_{\alpha=0.025}\frac{\sigma}{\sqrt{n}}
\end{align}
$$
また、上記において、標準正規分布$N(0, 1)$の表から、$z_{\alpha=0.025}=1.96$、$z_{\alpha=0.975}=-z_{\alpha=0.025}=-1.96$であることが読み取れることも抑えておくと良い。

・解説
「母分散既知の際の母平均の推定」は区間推定における最も基本的なトピックです。そのため、区間推定についてイメージがなかなかつかめない場合はとにかく「母分散既知の際の母平均の推定」の類題を確認すると良いと思います。

母平均の推定②（母分散未知）

・問題
i) $x_1, x_2, …, x_n$が得られた際の不偏標本分散$s^2$を求めよ。
ⅱ) $\displaystyle \frac{\bar{x}-\mu}{s/\sqrt{n}}$はどのような分布に従うか。
ⅲ) $\displaystyle \frac{\bar{x}-\mu}{s/\sqrt{n}}$の95％両側区間を求めよ。

・解答
i)
$s^2$は下記のように計算できる。
$$
\large
\begin{align}
s^2 &= \frac{1}{n-1}((x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2) \\
&= \frac{1}{n-1} \sum_{i=1}^{n} (x_i-\bar{x})^2
\end{align}
$$

ⅱ)
自由度$n-1$の$t$分布$t(n-1)$に従う。

ⅲ)
自由度$n-1$の$t$分布$t(n-1)$の上側確率を$p$とする点を$t_{\alpha=p}(n-1)$のように表すとする。この時、95％両側区間は下記のように求めることができる。
$$
\large
\begin{align}
t_{\alpha=0.975}(n-1) \leq &\frac{\bar{x}-\mu}{s/\sqrt{n}} \leq t_{\alpha=0.025}(n-1) \\
t_{\alpha=0.975}(n-1)\frac{s}{\sqrt{n}} \leq &\bar{x}-\mu \leq t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}} \\
-t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}} \leq &\mu-\bar{x} \leq -t_{\alpha=0.975}(n-1)\frac{s}{\sqrt{n}} \\
-t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}} \leq &\mu-\bar{x} \leq t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}} \\
\bar{x} – t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}} \leq &\mu \leq \bar{x} + t_{\alpha=0.025}(n-1)\frac{s}{\sqrt{n}}
\end{align}
$$

標準正規分布の分布表

・問題
標準正規分布$N(0,1)$の上側確率を$p$とする点を$z_{\alpha=p}$のように表すとする。この時、下記の値を分布表から読み取れ。
i) $z_{\alpha=0.5}$
ⅱ) $z_{\alpha=0.1}, z_{\alpha=0.9}$
ⅲ) $z_{\alpha=0.025}, z_{\alpha=0.975}$
ⅳ) $z_{\alpha=0.01}, z_{\alpha=0.99}$
ⅴ) $z_{\alpha=0.005}, z_{\alpha=0.995}$

・解答
i)
$$
\large
\begin{align}
z_{\alpha=0.5} = 0
\end{align}
$$

ⅱ)
$$
\large
\begin{align}
z_{\alpha=0.1} &= 1.28 \\
z_{\alpha=0.9} &= -1.28
\end{align}
$$

ⅲ)
$$
\large
\begin{align}
z_{\alpha=0.025} &= 1.96 \\
z_{\alpha=0.975} &= -1.96
\end{align}
$$

ⅳ)
$$
\large
\begin{align}
z_{\alpha=0.01} &= 2.32 \\
z_{\alpha=0.99} &= -2.32
\end{align}
$$

ⅴ)
$$
\large
\begin{align}
z_{\alpha=0.005} &= 2.58 \\
z_{\alpha=0.995} &= -2.58
\end{align}
$$

・解説
区間推定や検定などを行うにあたって、確率分布表を使い慣れているかどうかで難易度が大きく変わると思います。一見数字の羅列で難しそうではありますが、使い慣れることで問題を解きやすくなるのでとにかく慣れるのが良いと思います。

発展問題

参考書籍

・基礎統計学Ⅰ 統計学入門(東京大学出版会)