ブログ

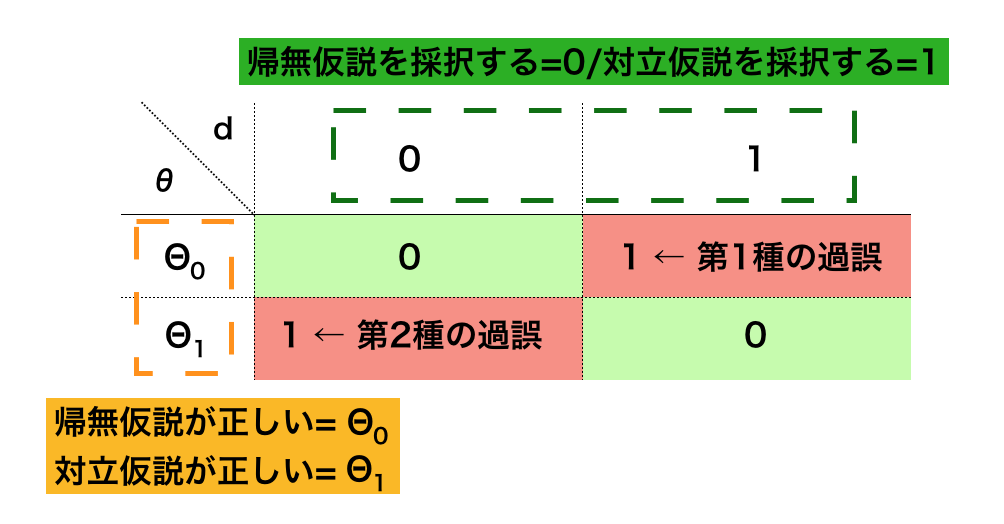
最尤法は観測値のみを元に推定を行うが、トピックによっては事前知識がわかっている場合や、サンプル数が少ない場合に最尤法が極端な結果を示す場合の補正にあたって、事前分布に基づくベイズ法は役に立つ。事前分布やMAP推定、予測分布が理解できるように演習を取り扱った。
・現代数理統計学　Ch.$14$ 「ベイズ法」の章末演習の解答例
https://www.hello-statisticians.com/explain-books-cat/math_stat_practice_ch14.html

・標準演習$100$選
https://www.hello-statisticians.com/practice_100

基本問題

ベイズの定理と事前分布・事後分布

・問題
パラメータ推定におけるベイズの定理の導入は「ベイズ統計」や「ベイズ推定」など様々な表現があるが、数式に基づく基本的な流れを抑えておけば基本的に十分である。この問題では以下、最尤推定に対し事前分布を元にベイズの定理を考える一連の流れについて取り扱う。下記の問いにそれぞれ答えよ。

i) 事象$A,B$がある際に、$A \cap B$は条件付き確率を元に下記のように表せる。
$$
\begin{align}
P(A \cap B) = P(A|B)P(B) = P(B|A)P(A) \quad (1)
\end{align}
$$

上記の式が妥当であることを直感的に解釈せよ。

ⅱ) $(1)$式より、$P(A|B)$を$P(B), P(B|A), P(A)$を用いて表せ。

ⅲ) ⅱ)の式がベイズの定理の式に一致する。以下ではベイズの定理を最尤法に適用する流れに関して二項分布を例に確認を行う。$X \sim \mathrm{Bin}(n,p)$の確率関数$p(x)=P(x|p)$は下記のように表せる。
$$
\begin{align}
p(x) = {}_{n} C_{x} p^{x} (1-p)^{n-x} \quad (2)
\end{align}
$$

ここで$n$回のベルヌーイ試行に基づいて観測値$X=x$が得られた際に$p$の推定を行うことを考える。最尤推定は尤度を$L(p)=P(x|p)$とおき、$L(p)$が最大になる$p$を導出する手法である。
$(2)$式を元に対数を考えることで、$L(p)$が最大値を取る$p$を$x, n$を用いて表せ。

iv) $n=2$のとき、ⅲ)の式を用いて$x=0,1,2$に関して$p$の推定を行え。

v) $n=2$のようにサンプルが少ない場合、iv)の推定結果は$x$の値次第で大きく変動する。この変動の緩和にあたって下記のように事前分布$P(p)$を導入することを考える。
$$
\begin{align}
P(p) = 6p(1-p), \quad 0 \leq p \leq 1
\end{align}
$$

ここで$P(x)=c(x)$のように表すとき、ベイズの定理に基づいて事後分布$P(p|x)$を表せ。

vi) v)で得られた事後分布$P(p|x)$が最大になる$p$を$n, x$を用いて表せ。
vⅱ) $n=2$のときvi)の式を用いて$x=0,1,2$に関しての$p$の推定を行い、事前分布や事後分布を導入した意義に関して論じよ。

・解答
i)
$(1)$式は「$2$つの事象が同時に発生する確率」と「どちらか一方が発生し、その後にもう一方が発生する確率」のどちらで考えても式が同様であると直感的に解釈できる。

ⅱ)
下記のように表せる。
$$
\large
\begin{align}
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
\end{align}
$$

ⅲ)
対数尤度$\log{L(p)}=\log{P(x|p)}$は下記のように考えることができる。
$$
\large
\begin{align}
\log{L(p)} &= \log{P(x|p)} \\
&= \log{({}_{n} C_{x} p^{x} (1-p)^{n-x})} \\
&= x \log{p} + (n-x) \log{(1-p)} + \log{{}_{n} C_{x}}
\end{align}
$$

iv)
ⅲ)の結果に$n=2$と$x=0,1,2$を代入することで$\hat{p}=0, \hat{p}=0.5, \hat{p}=1$がそれぞれ得られる。

v)
ベイズの定理に基づいて事後分布$P(p|x)$は下記のように表せる。
$$
\large
\begin{align}
P(p|x) &= \frac{P(x|p)P(p)}{P(x)} \\
&= \frac{6 {}_{n} C_{x}}{c(x)} p^{x+1} (1-p)^{n-x+1}
\end{align}
$$

vi)
事後分布の対数$\log{P(p|x)}$は下記のように表せる。
$$
\large
\begin{align}
\log{P(p|x)} &= \log{ \left[ \frac{6 {}_{n} C_{x}}{c(x)} p^{x+1} (1-p)^{n-x+1} \right] } \\
&= (x+1) \log{p} + (n-x+1) \log{(1-p)} + \log{ \left[ \frac{6 {}_{n} C_{x}}{c(x)} \right] }
\end{align}
$$

上記を$p$に関して微分すると下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{P(p|x)}}{\partial p} &= \frac{x+1}{p} – \frac{n-x+1}{1-p} \\
&= \frac{(x+1)(1-p) – (n-x+1)p}{p(1-p)} \\
&= \frac{x+1-(n+2)p}{p(1-p)}
\end{align}
$$

上記は$p$に関して単調増加であるので、$\log{L(p)}$や$L(p)$は$\displaystyle p = \frac{x+1}{n+2}$のとき最大値を取る。

vⅱ)
vi)の結果に$n=2$と$x=0,1,2$を代入することで$\hat{p}=0.25, \hat{p}=0.5, \hat{p}=0.75$がそれぞれ得られる。ここでiv)では$\hat{p}=0, \hat{p}=0.5, \hat{p}=1$が得られたことを鑑みると、事前分布を導入することで$0.5$に近い推定結果が得られたことが確認できる。
このように事前分布を導入することでサンプル数が少ない場合のサンプルのばらつきに対して頑健である結果が得られることが多い。

・解説
この問題では「二項分布の共役事前分布」を題材にベイズの定理と事前分布・事後分布に関して確認を行いました。詳しい内容は「二項分布の共役事前分布と事後分布の解釈」で取り扱いました。
vⅱ)では事前分布を導入した意義に関して論じましたが、$p=0.5$に近い値の場合は妥当である一方で$p=0.01$や$p=0.99$の場合には妥当でない結果になり得ることに注意が必要です。手法選択の際には一見ベイズ手法が万能であるように見えがちですが、「ベイズ推定は最尤推定よりも必ず良い」ではなく、「妥当な事前分布が設定できる場合はサンプルが少ない際に有用である」のように理解しておくのが良いように思います。

二項分布の共役事前分布と事後分布の解釈

・問題
共役事前分布(conjugate prior distribution)を用いることで、事後分布の導出をシンプルに行うことができる。共役事前分布はフォーマルな表記だと難しい印象があると思われるので、以下では二項分布を例に共役事前分布について確認し、事後分布の解釈を行う。

ベイズ法ではパラメータの推定にあたって、下記のように事後分布の$P(\theta|x)$が事前分布の$P(\theta)$と尤度の$p(x|\theta)$の積に比例することを利用する。
$$
\large
\begin{align}
P(\theta|x) \propto P(\theta)p(x|\theta) \quad (1)
\end{align}
$$

上記の式は多くの書籍などで出てくるが、抽象的な表記より具体的な確率分布を例に考える方がわかりやすい。以下では二項分布に関して$(1)$式を表すことを考える。

ここまでの内容を元に下記の問いに答えよ。
i) 二項分布におけるパラメータは事象が起こる確率であるので、以下では$\theta=p$のように、パラメータを$\theta$ではなく$p$を用いて表す。確率$p$の試行を$n$回繰り返すとき、事象が起こる回数を$x$、この確率関数を$p(x|p,n)$のように表すとき、確率関数$p(x|p,n)$の式を表せ。
ⅱ) ベータ分布$Be(a,b)$の確率密度関数を答えよ。
ⅲ) i)で取り扱った確率関数$p(x|p,n)$は尤度と考えることができる。ここで$p(x|p,n)$を$x$ではなく$p$の関数と見るときベータ分布と同様の形を持つことをⅱ)の結果と見比べることで示せ。
iv) $p$の事前分布の$P(p)$がベータ分布$Be(a,b)$であるとき、事前分布$P(p)$の関数を記載せよ。
v) $p(x|p,n)P(p)$を計算せよ。
vi) 事後分布$P(p|x)$が$P(p|x) \propto p(x|p,n)P(p)$のように表されることを元に、事後分布$P(p|x)$がどのような分布になるか答えよ。
vⅱ) v)、vi)の結果を確認することでベータ分布$Be(a,b)$の$a,b$のこの事例での意味を考察せよ。

・解答
i)
確率関数$p(x|p,n)$は下記のように表すことができる。
$$
\large
\begin{align}
p(x|p,n) = {}_{n} C_{x} p^{x} (1-p)^{n-x}
\end{align}
$$

ⅱ)
ベータ分布$Be(a,b)$の確率密度関数を$f(x|a,b)$とおくとき、$f(x|a,b)$は下記のように表される。
$$
\large
\begin{align}
f(x|a,b) = \frac{1}{B(a,b)} x^{a-1} (1-x)^{b-1}
\end{align}
$$
ここで上記における$B(a,b)$はベータ関数を表す。

ⅲ)
i)とⅱ)の結果を見比べることで、どちらも変数を$x$と見た際に、$x^{a-1} (1-x)^{b-1}$の形状の関数であることを読み取ることができる。

iv)
事前分布$P(p)$はⅱ)の結果の$x$を$p$で置き換えることで得られるので、下記のように表すことができる。
$$
\large
\begin{align}
P(p) = \frac{1}{B(a,b)} p^{a-1} (1-p)^{b-1}
\end{align}
$$

v)
$p(x|p,n)P(p)$は下記のように計算できる。
$$
\large
\begin{align}
p(x|p,n)P(p) &= {}_{n} C_{x} p^{x} (1-p)^{n-x} \times \frac{1}{B(a,b)} p^{a-1} (1-p)^{b-1} \\
&= \frac{{}_{n} C_{x}}{B(a,b)} p^{a+x-1} (1-p)^{b+n-x-1}
\end{align}
$$

vi)
v)の結果より、下記が成立する。
$$
\large
\begin{align}
P(p|x) & \propto p(x|p,n)P(p) \\
&= {}_{n} C_{x} p^{x} (1-p)^{n-x} \times \frac{1}{B(a,b)} p^{a-1} (1-p)^{b-1} \\
& \propto p^{a+x-1} (1-p)^{b+n-x-1}
\end{align}
$$
よって事後分布$P(p|x)$はベータ分布$Be(a+x,b+n-x)$に一致する。

vⅱ)
二項分布における$x, n-x$はコイン投げにおける表と裏の回数に一致する。事前分布における$(a,b)$が事後分布において$(a+x,b+n-x)$になることは、実際の実験を行う前に事前に表が$a$回、裏が$b$回出たと考えることに一致する。

・解説
vⅱ)より、事前分布のベータ分布におけるパラメータの$a, b$に事前知識を組み込むことが可能になります。このようにすることで、試行回数が$5$回や$10$回などの少ない際に事前知識による補正ができると抑えておくと良いと思います。

ポアソン分布の共役事前分布と事後分布の解釈

・問題
ポアソン分布の共役事前分布にはガンマ分布を考えることができるので、ガンマ分布の解釈と合わせて理解すれば良い。以下、導出の流れとガンマ分布の解釈に関して確認を行う。

ポアソン分布の確率関数を$f(x|\lambda)$とおくと、$f(x|\lambda)$は下記のように表される。
$$
\begin{align}
f(x|\lambda) = \frac{\lambda^{x} e^{-\lambda}}{x!} \\
\end{align}
$$

ここで観測値$x_1, x_2, …, x_n$が観測される同時確率を$P(x_1,…,x_n|\lambda)$とおくと、$P(x_1,…,x_n|\lambda)$は下記のように表すことができる。
$$
\begin{align}
P(x_1,…,x_n|\lambda) &= \prod_{i=1}^{n} \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \\
&= \lambda^{\sum_{i=1}^{n} x_i} e^{-n \lambda} \prod_{i=1}^{n} (x_i!)^{-1} \\
&= \lambda^{n \bar{x}} e^{-n \lambda} \prod_{i=1}^{n} (x_i!)^{-1}
\end{align}
$$

上記を$\lambda$の関数と見ると、ガンマ分布の形状と一致するので、$\lambda$の事前分布$P(\lambda)$に$Ga(a,1)$を考える。このとき$P(\lambda)$は下記のように表すことができる。
$$
\begin{align}
P(\lambda) = \frac{1}{\Gamma(a)} \lambda^{a-1} e^{-\lambda}
\end{align}
$$

ここまでの内容を元に以下の問題に答えよ。
i) 事後分布$P(\lambda|x_1,x_2,…,x_n) \propto P(x_1,…,x_n|\lambda)P(\lambda)$を計算せよ。ただし、$\propto$を用いて$\lambda$に関連しない項は省略して良い。
ⅱ)
$$
\begin{align}
f(x|a,b) = \frac{b^a}{\Gamma(a)} \lambda^{a-1} e^{-b \lambda}
\end{align}
$$
$Ga(a,b)$の確率密度関数$f(x|a,b)$が上記のように表されるとき、i)の結果より、$\lambda$の事後分布$P(\lambda|x_1,x_2,…,x_n)$がどのようなパラメータのガンマ分布に従うか答えよ。
ⅲ) ガンマ分布$Ga(a,b)$のモーメント母関数を$m(t)$のようにおくと、$\lambda > t$のとき$m(t)$は下記のように表すことができる。
$$
\begin{align}
m(t) = \left( \frac{b}{b-t} \right)^{a}
\end{align}
$$
上記に対し、$\displaystyle \frac{d}{dt}m(t), \frac{d^2}{dt^2}m(t)$を導出せよ。
iv) ⅲ)の結果を元にガンマ分布$Ga(a,b)$の期待値$E[\lambda]$と分散$V[\lambda]$を計算せよ。
v) ⅱ)とiv)の結果を元に、観測値が観測されるにつれて事後分布は事前分布に比べてどのように変化するかを考察せよ。

・解答
i)
下記のように事後分布$P(\lambda|x_1,x_2,…,x_n)$に関して計算を行うことができる。
$$
\large
\begin{align}
P(\lambda|x_1,x_2,…,x_n) & \propto P(x_1,…,x_n|\lambda)P(\lambda) \\
&= \lambda^{n \bar{x}} e^{-n \lambda} \prod_{i=1}^{n} (x_i!)^{-1} \times \frac{1}{\Gamma(a)} \lambda^{a-1} e^{-\lambda} \\
& \propto \lambda^{a + n \bar{x} – 1} e^{-(n+1) \lambda}
\end{align}
$$

ⅱ)
事後分布$P(\lambda|x_1,x_2,…,x_n)$はガンマ分布$Ga(a + n \bar{x}, n+1)$のガンマ分布に従う。

ⅲ)
$\displaystyle \frac{d}{dt}m(t), \frac{d^2}{dt^2}m(t)$は下記のように計算できる。
$$
\large
\begin{align}
\frac{d}{dt}m(t) &= \frac{d}{dt} \left( \frac{b}{b-t} \right)^{a} \\
&= b^a \frac{d}{dt} (b-t)^{-a} \\
&= b^a \times -a(b-t)^{-a-1} \times (-1) = \frac{ab^{a}}{(b-t)^{a+1}} \\
\frac{d^2}{dt^2}m(t) &= \frac{d}{dt} \left( \frac{ab^{a}}{(b-t)^{a+1}} \right) \\
&= ab^{a} \frac{d}{dt} (b-t)^{-(a+1)} \\
&= ab^{a} \times -(a+1) (b-t)^{-(a+2)} \times (-1) = \frac{a(a+1)b^{a}}{(b-t)^{a+2}}
\end{align}
$$

iv)
期待値$E[\lambda]$と分散$V[\lambda]$は下記のように計算することができる。
$$
\large
\begin{align}
E[\lambda] &= \frac{d}{dt}m(t) \Bigr|_{t=0} \\
&= \frac{ab^{a}}{(b-0)^{a+1}} \\
&= \frac{a}{b} \\
V[\lambda] &= \frac{d^2}{dt^2}m(t) \Bigr|_{t=0} – \left( \frac{d}{dt}m(t) \Bigr|_{t=0} \right)^{2} \\
&= \frac{a(a+1)b^{a}}{(b-0)^{a+2}} – \left( \frac{a}{b} \right)^{2} \\
&= \frac{a(a+1)}{b^2} – \frac{a^2}{b^2} \\
&= \frac{a^2+a-a^2}{b^2} \\
&= \frac{a}{b^2}
\end{align}
$$

v)
iv)の結果を元にⅱ)で確認を行なった事前分布$Ga(a, 1)$と事後分布$Ga(a + n \bar{x}, n+1)$を確認する。事前分布の期待値・分散をそれぞれ$E[\lambda], V[\lambda]$、事後分布の期待値・分散をそれぞれ$E[\lambda|x_1,x_2,…,x_n], V[\lambda|x_1,x_2,…,x_n]$とおく。$E[\lambda], E[\lambda|x_1,x_2,…,x_n], V[\lambda], V[\lambda|x_1,x_2,…,x_n]$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
E[\lambda] &= \frac{a}{1} = a \\
E[\lambda|x_1,x_2,…,x_n] &= \frac{a + n \bar{x}}{n+1} \\
V[\lambda] &= \frac{a}{1^2} = a \\
V[\lambda|x_1,x_2,…,x_n] &= \frac{a + n \bar{x}}{(n+1)^2}
\end{align}
$$

上記より、$n$が大きくなるにつれて$E[\lambda], E[\lambda|x_1,x_2,…,x_n]$が標本平均の$\bar{x}$に近づき、$V[\lambda], E[\lambda|x_1,x_2,…,x_n]$が$0$に近づくことがわかる。

これは$n$が大きくなるにつれて最尤推定の結果に近づくことを意味し、ベイズの定理を用いた推定が最尤法の拡張であると考えることができることを表している。

・解説
主に下記の内容に基づいて作成を行いました。
https://www.hello-statisticians.com/explain-terms-cat/conjugate_dist1.html

ⅲ)で取り扱ったガンマ分布のモーメント母関数に関しては下記で詳しい導出を行いましたので、こちらも参考になると思います。
https://www.hello-statisticians.com/explain-books-cat/toukeigaku-aohon/ch1_blue_practice.html#19

v)の結果の解釈は最尤法とベイズを比較する際によく出てくるので、事後分布を用いた推定結果の解釈に関してはなるべく行うようにすると良いと思います。

正規分布の共役事前分布の設定と事後分布

・問題
観測値が正規分布に従うと仮定した際の尤度のパラメータに対して正規分布の共役事前分布を考えることで、ベイズの定理を用いて事後分布を計算することができる。

この計算は重要なトピックである一方で平方完成に関連する計算が複雑になり、計算ミスなどが起こりやすい。この問題では以下、関連の計算について可能な限りシンプルに計算ができるように導出の流れの確認を行う。

以下の問題に答えよ。
i) 正規分布$\mathcal{N}(\mu, \sigma^2)$の確率密度関数を$f(x|\mu,\sigma^2)$のようにおくとき、$f(x|\mu,\sigma^2)$を$x, \mu, \sigma^2$の式で表せ。
ⅱ) 確率変数列${X_1,…,X_n}$に対して$X_1,…,X_n \sim \mathcal{N}(\mu, \sigma^2) \quad i.i.d.,$が成立するとき、確率変数列$\{X_1,…,X_n\}$に対応する観測値の列$\{x_1,…,x_n\}$が観測されたときの$\mu$に関する尤度$L(\mu|x_1,…,x_n)$を表せ。
ⅲ) $\displaystyle \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$のようにおくとき、Fisher-Neymanの分解定理を用いて$\bar{x}$が$\mu$の十分統計量であることを示せ。
iv) $\mu$の事前分布が正規分布$\mathcal{N}(\lambda,\tau^2)$に従うとき、確率密度関数$P(\mu)$を$\lambda,\tau^2$を用いて表せ。
v) $a>0$のとき$g(x) = ax^2 + bx + c$の平方完成を行え。また、$g(x)$が最小となる$x$の値を答えよ。
vi) $x_1,x_2,…,x_n$が観測された際の$\mu$の事後分布の確率密度関数$P(\mu|x_1,…,x_n)$をベイズの定理に基づいて計算し、事後分布が$\displaystyle \mathcal{N} \left( \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} , \frac{\sigma^2 \tau^2}{n \tau^2 + \sigma^2} \right)$に一致することを確認せよ。
vⅱ) vi)の結果を事後分布の平均に着目して解釈せよ。

・解答
i)
確率密度関数$f(x|\mu,\sigma^2)$は下記のように表すことができる。
$$
\large
\begin{align}
f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left[ -\frac{(x-\mu)^2}{2 \sigma^2} \right]
\end{align}
$$

ⅱ)
尤度$L(\mu|x_1,…,x_n)$は同時確率に一致するので、$i.i.d.,$であることから下記のように導出することができる。
$$
\large
\begin{align}
L(\mu|x_1,…,x_n) &= f(x_1,…,x_n|\mu,\sigma^2) = \prod_{i=1}^{n} f(x_i|\mu,\sigma^2) \\
&= \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left[ -\frac{(x_i-\mu)^2}{2 \sigma^2} \right] \\
&= \left( \frac{1}{\sqrt{2 \pi} \sigma} \right)^{n} \exp \left[ -\sum_{i=1}^{n} \frac{(x_i-\mu)^2}{2 \sigma^2} \right]
\end{align}
$$

ⅲ)
$(x_i-\mu) = (x_i-\bar{x}) + (\bar{x}-\mu)$より、 $\displaystyle \sum_{i=1}^{n} (x_i-\mu)^2$は下記のように変形できる。
$$
\large
\begin{align}
\sum_{i=1}^{n} (x_i-\mu)^2 &= \sum_{i=1}^{n} ((x_i-\bar{x}) + (\bar{x}-\mu))^2 \\
&= \sum_{i=1}^{n} ((x_i-\bar{x})^2 + 2(\bar{x}-\mu)^2 + (x_i-\bar{x})(\bar{x}-\mu)) \\
&= \sum_{i=1}^{n} (x_i-\bar{x})^2 + \sum_{i=1}^{n} (\bar{x}-\mu)^2 + 2(\bar{x}-\mu) \sum_{i=1}^{n}(x_i-\bar{x}) \\
&= \sum_{i=1}^{n} (x_i-\bar{x})^2 + \sum_{i=1}^{n} (\bar{x}-\mu)^2 \\
&= n(x_i-\bar{x})^2 + \sum_{i=1}^{n} (\bar{x}-\mu)^2
\end{align}
$$

よって同時確率密度関数$f(x_1,…,x_n|\mu,\sigma^2)$は下記のように変形できる。
$$
\large
\begin{align}
f(x_1,…,x_n|\mu,\sigma^2) &= \prod_{i=1}^{n} f(x_i|\mu,\sigma^2) \\
&= \left( \frac{1}{\sqrt{2 \pi} \sigma} \right)^{n} \exp \left[ -\sum_{i=1}^{n} \frac{(x_i-\mu)^2}{2 \sigma^2} \right] \\
&= \exp \left[ -\frac{n(\bar{x}-\mu)^2}{2 \sigma^2} \right] \times \left( \frac{1}{\sqrt{2 \pi} \sigma} \right)^{n} \exp \left[ -\sum_{i=1}^{n} \frac{(x_i-\bar{x})^2}{2 \sigma^2} \right]
\end{align}
$$

上記のように同時確率密度関数を$\mu, \bar{x}$の関数と$x_i,\bar{x}$の関数に分解することができたのでFisher-Neymanの定理より$\bar{x}$が$\mu$の十分統計量であることが示せる。

iv)
確率密度関数$P(\mu)$は下記のように表せる。
$$
\large
\begin{align}
f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2 \pi} \tau} \exp \left[ -\frac{(\mu-\lambda)^2}{2 \tau^2} \right]
\end{align}
$$

v)
下記のように$g(x)$の平方完成を行うことができる。
$$
\large
\begin{align}
g(x) &= ax^2+bx+c \\
&= a \left( x^2 + \frac{b}{a}x \right) + c \\
&= a \left( x + \frac{b}{2a} \right)^2 + c – a \left( \frac{b}{2a} \right)^2 \\
&= a \left( x + \frac{b}{2a} \right)^2 + c – \frac{ab^2}{4a^2} \\
&= a \left( x + \frac{b}{2a} \right)^2 + c – \frac{b^2}{4a}
\end{align}
$$

$g(x)$は$a>0$から下に凸の関数であるので、上記より、$\displaystyle x = -\frac{b}{2a}$のとき$g(x)$は最小値を取ることがわかる。

vi)
事後分布の確率密度関数$P(\mu|x_1,…,x_n)$に関しては下記のように考えることができる。
$$
\large
\begin{align}
P(\mu|x_1,…,x_n) & \propto L(\mu|x_1,…,x_n) P(\mu) \\
&= \exp \left[ -\frac{n(\bar{x}-\mu)^2}{2 \sigma^2} \right] \times \left( \frac{1}{\sqrt{2 \pi} \sigma} \right)^{n} \exp \left[ -\sum_{i=1}^{n} \frac{(x_i-\bar{x})^2}{2 \sigma^2} \right] \times \frac{1}{\sqrt{2 \pi} \tau} \exp \left[ -\frac{(\mu-\lambda)^2}{2 \tau^2} \right] \\
& \propto \exp \left[ -\frac{n(\bar{x}-\mu)^2}{2 \sigma^2} \right] \times \exp \left[ -\frac{(\mu-\lambda)^2}{2 \tau^2} \right] \\
&= \exp \left[ -\frac{\sigma^2(\mu-\lambda)^2 + n \tau^2(\mu-\bar{x})^2}{2 \sigma^2 \tau^2} \right] \\
&= \exp \left[ -\frac{(n \tau^2 + \sigma^2)\mu^2 – 2(n \tau^2 \bar{x} + \sigma^2 \lambda)\mu + …}{2 \sigma^2 \tau^2} \right] \\
& \propto \exp \left[ -\frac{n \tau^2 + \sigma^2}{2 \sigma^2 \tau^2} \left(\mu – \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} \right)^2 \right]
\end{align}
$$

vⅱ)
$\displaystyle \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2}$を解釈するにあたっては、標本平均$\bar{x}$と事前分布の平均の$\lambda$がそれぞれどのような配分で事後分布の平均に作用するかを確認すればよい。

ここで事後分布の平均は$\bar{x}$と$\lambda$を$n \tau^2:\sigma^2$に内分する点であることが確認でき、$n$が大きい時は$\bar{x}$に限りなく近づくことも同時にわかる。

・解説
下記の内容に基づいて作成を行いました。
https://www.hello-statisticians.com/explain-terms-cat/conjugate_dist1.html#i-6

ⅲ)のようにFisher-Neymanの定理の式の形で同時確率密度関数、尤度を表すことで$\mu$に関連する部分の表記をシンプルに行えます。このような表記を用いることで、vi)での計算で$\displaystyle \sum$を考えなくてよく、これにより式が見やすくなります。

vi)の計算にあたってはv)のように全ての項を考えるのではなく、v)の結果を活用しさらに$\propto$を用いて定数項は考えないことで計算をシンプルに行うことができます。

EAP推定量とMAP推定量

・問題
ベイズの定理を用いてパラメータの事後分布を得た場合、予測分布のように事後分布をそのまま用いる場合もあるが、事後分布を$1$つの値に要約して用いる場合も多い。この要約にあたっては事後分布の期待値を考えるEAP推定量と事後分布が最大となる点に着目するMAP推定量がよく用いられる。EAP推定量は期待事後推定量(Expected a Posterior Estimator)の略で、MAP推定量は最大事後確率推定量(Maximum a Posterior Estimator)の略であることも合わせて抑えておくと良い。

この問題では以下、EAP推定量とMAP推定量に関して具体的な事後分布に基づいて確認するにあたって、「ベータ分布」、「ガンマ分布」、「正規分布」に対してそれぞれEAP推定量とMAP推定量の導出を行う。「ベータ分布$\mathrm{Be}(\alpha,\beta)$」、「ガンマ分布$\mathrm{Ga}(\alpha,\beta)$」、「正規分布$\mathcal{N}(\mu,\sigma^2)$」の確率密度関数を$f_1(x),f_2(x),f_3(x)$とおくとそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
f_1(x) &= \frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1} = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} \\
f_2(x) &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} \exp{\left( -\frac{x}{\beta} \right)} \\
f_3(x) &= \frac{1}{\sqrt{2 \pi \sigma^2}} \exp{\left( -\frac{(x-\mu)^2}{2 \sigma^2} \right)}
\end{align}
$$

ここまでの内容に基づいて下記の問いにそれぞれ答えよ。
i) EAP推定量とMAP推定量は記述統計における「代表値」と対応して理解することができるが、EAP推定量とMAP推定量はそれぞれどのような代表値に対応するか答えよ。
ⅱ) 「二項分布の共役事前分布と事後分布の解釈」では、二項分布$\mathrm{Bin}(n,p)$の確率パラメータ$p$の事後分布にベータ分布$\mathrm{Be}(\alpha+x,\beta+n-x)$が得られた。このとき$p$のEAP推定量$\hat{p}_{EAP}$とMAP推定量$\hat{p}_{EAP}$を$n,x,\alpha,\beta$を用いて表せ。
ⅲ) ⅱ)と同様に事後分布にベータ分布$\mathrm{Be}(\alpha+x,\beta+n-x)$が得られたとき、$p$のMAP推定量$\hat{p}_{MAP}$を$n,x,\alpha,\beta$を用いて表せ。
iv) ⅱ)、ⅲ)で得られた$\hat{p}_{EAP}$と$\hat{p}_{MAP}$を最尤推定量$\displaystyle \hat{p}_{MLE}=\frac{x}{n}$に基づいて解釈せよ。
v) $\lambda \sim \mathrm{Ga}(\alpha,\beta)$のとき、$\hat{\lambda}_{EAP}$と$\hat{\lambda}_{MAP}$をそれぞれ計算せよ。
vi) $\mu \sim \mathcal{N}(\mu_N,\sigma_N^2)$のとき、$\hat{\mu}_{EAP}$と$\hat{\mu}_{MAP}$をそれぞれ答えよ。

・解答
i)
EAP推定量は平均に対応し、MAP推定量はモードに対応すると考えることができる。

ⅱ)
$p$のEAP推定量$\hat{p}_{EAP}$は下記のように得られる。
$$
\large
\begin{align}
\hat{p}_{EAP} &= \int_{0}^{1} p \times f_1(p) dp \\
&= \frac{1}{B(a+x,\beta+n-x)} \int_{0}^{1} p \times p^{\alpha+x-1} (1-p)^{\alpha+n-x-1} dp \\
&= \frac{1}{B(a+x,\beta+n-x)} \int_{0}^{1} p^{\alpha+x+1-1} (1-p)^{\alpha+n-x-1} dp \\
&= \frac{B(a+x+1,\beta+n-x)}{B(a+x,\beta+n-x)} \\
&= \frac{\Gamma(\alpha+x+1)\Gamma(\beta+n-x)}{\Gamma(n+\alpha+\beta+1)} \times \frac{\Gamma(n+\alpha+\beta)}{\Gamma(\alpha+x)\Gamma(\beta+n-x)} \\
&= \frac{(\alpha+x)!(\beta+n-x-1)!}{(n+\alpha+\beta)!} \times \frac{(n+\alpha+\beta-1)!}{(\alpha+x-1)!(\beta+n-x-1)!} \\
&= \frac{\alpha+x}{n+\alpha+\beta}
\end{align}
$$

ⅲ)
$p$のMAP推定量$\hat{p}_{MAP}$は下記のように得られる。
$$
\large
\begin{align}
\frac{\partial \log{(P(p|x))}}{\partial p} &= \frac{\partial}{\partial p} \log{\left[ \frac{1}{B(\alpha+x-1,\beta+n-x)} p^{\alpha+x-1}(1-p)^{\beta+n-x-1} \right]} \\
&= \frac{\partial}{\partial p} \left[ (\alpha+x-1)\log{p} + (\beta+n-x-1)\log{(1-p)} – \log{B(\alpha+x-1,\beta+n-x)} \right] \\
&= \frac{\alpha+x-1}{p} – \frac{\beta+n-x-1}{1-p} \\
&= \frac{(\alpha+x-1)(1-p) – (\beta+n-x-1)p}{p(1-p)} \\
&= \frac{\alpha+x-1 – (n+\alpha+\beta-2)p}{p(1-p)} \\
\hat{p}_{MAP} &= \frac{\alpha+x-1}{n+\alpha+\beta-2}
\end{align}
$$

iv)
最尤推定量$\displaystyle \hat{p}_{MLE}=\frac{x}{n}$は$n$回の試行の中で事象が$x$回観測されたのでパラメータを$\displaystyle \hat{p}_{MLE}=\frac{x}{n}$のように推定したと考えられる。
事後分布に基づく推定は予めサンプルがある上で観測された割合を計算したと見ることもでき、EAP推定量は「事前に$\alpha+\beta$回中$\alpha$回計測された場合」、MAP推定量は「事前に$\alpha+\beta-2$回中$\alpha-1$回計測された場合」とそれぞれ解釈できる。

v)
$\hat{\lambda}_{EAP}$は下記のように計算できる。
$$
\large
\begin{align}
\hat{\lambda}_{EAP} &= \int_{0}^{\infty} \lambda \times f_2(\lambda) d \lambda \\
&= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_{0}^{\infty} \lambda \times \lambda^{\alpha-1} \exp{\left( -\frac{\lambda}{\beta} \right)}d \lambda \\
&= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_{0}^{\infty} \lambda^{(\alpha+1)-1} \exp{\left( -\frac{\lambda}{\beta} \right)}d \lambda \\
&= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \times \beta{\alpha+1} \Gamma(\alpha+1) \\
&= \alpha \beta
\end{align}
$$

$\hat{\lambda}_{MAP}$の計算にあたっては$\log{f_2(\lambda)}$を考え、$\lambda$で微分を行えばよい。$\log{f_2(\lambda)}$は下記のように表すことができる。
$$
\large
\begin{align}
\log{f_2(\lambda)} &= \log{ \left[ \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \lambda^{\alpha-1} \exp{\left( -\frac{\lambda}{\beta} \right)} \right] } \\
&= (\alpha-1) \log{\lambda} – \frac{\lambda}{\beta} – \log{\left[ \beta^{\alpha} \Gamma(\alpha) \right]}
\end{align}
$$

上記を$\lambda$で偏微分を行うことで下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{f_2(\lambda)}}{\partial \lambda} &= \frac{\alpha-1}{\lambda} – \frac{1}{\beta} \\
&= \frac{\alpha \beta – \beta – \lambda}{\lambda \beta} \\
\hat{\lambda}_{MAP} &= (\alpha-1) \beta
\end{align}
$$

vi)
正規分布の確率密度関数の形状より、$\hat{\mu}_{EAP}=\mu_N, \hat{\mu}_{MAP}=\mu_N$である。

・解説
ⅱ)〜iv)では二項分布の確率パラメータ$p$の事後分布に基づいてEAP推定量、MAP推定量の計算を行いました。v)、vi)の事後分布のパラメータはそれぞれ「ポアソン分布の共役事前分布と事後分布の解釈」と「正規分布の共役事前分布の設定と事後分布」で取り扱いました。ⅱ)〜iv)では事後分布のパラメータを元に推定量の計算を行いましたが、このように計算すると式が複雑になるので、v)、vi)のように「①それぞれの確率分布に関する推定量の計算」と「②事後分布のパラメータの計算」を分けて考えるとシンプルに取り扱えて良いのではないかと思います。v)、vi)では簡略化にあたって②は省略し、①のみ取り扱いました。
また、EAP推定量は積分、MAP推定量は微分を用いることでそれぞれ計算できることは抑えておくと良いと思います。
「統計検定準$1$級のワークブック」ではEAP推定量を「ベイズ推定量」のように表現されますが、ベイズ推定が何を指すのかがわかりにくくなるので、この問題では「数理統計学 統計的推論の基礎」に基づいて「EAP推定量」と表記しました。

発展問題

共役事前分布と指数型分布族

予測分布

・問題
パラメータ$\theta$に関する事後分布は観測された標本$x_1,\cdots,x_n$を元に$P(\theta|x_1,\cdots,x_n)$を考える。ここで得られた事後分布を元に新規の標本に関して予測を行うことを考える。

予測を行うにあたっては、「EAP推定量とMAP推定量」で考えたように事後分布を元にパラメータの推定量を計算し、推定量を元に予測を行うのがシンプルである。が、新規のサンプル$x_{n+1}$に関して下記を考えることで予測を行うことも可能である。
$$
\large
\begin{align}
P(x_{n+1}|x_1,\cdots,x_n) = \int P(x_{n+1}|\theta) P(\theta|x_1,\cdots,x_n) d \theta
\end{align}
$$

上記に基づいて定められる$P(x_{n+1}|x_1,\cdots,x_n)$を予測分布(Predictive distribution)という。以下、標本がポアソン分布に基づいて観測された際の予測分布の導出に関して演習形式で確認を行う。下記の問いにそれぞれ答えよ。
i) ポアソン分布$\mathrm{Po}(\lambda)$の確率関数を$p(x)$とおくとき、$p(x)$を$x, \lambda$の式で表せ。
ⅱ) $x_1=2, x_2=3, x_3=5, x_4=2, x_5=3$が観測されたとき、i)の式を元に尤度$L(\lambda)$を表せ。
ⅲ) パラメータ$\lambda$の事前分布にガンマ分布$\displaystyle \mathrm{Ga} \left( 3,\frac{1}{2} \right)$を考える。この確率密度関数を$P(\lambda)$とおくとき$P(\lambda)$を表せ。
iv) ⅱ)の尤度$L(\lambda)=P(x_1,\cdots,x_5|\lambda)$とⅲ)の事前確率$P(\lambda)$を用いて$\lambda$の事後分布を求めよ。
v) iv)で求めた事後分布の確率密度関数$P(\lambda|x_1,\cdots,x_5)$を表せ。
vi) v)の結果などを用いて$(1)$式を元に$P(x_{n+1}|x_1,\cdots,x_5)$を計算せよ。
vⅱ) 負の二項分布$\mathrm{NB}(r,p)$の確率関数を$p(x)$とおくと、$p(x)$は下記のように表せる。
$$
\begin{align}
p(x) &= {}_r H_{x} p^{r} (1-p)^{x} \\
&= {}_{r+x-1} C_{x} p^{r} (1-p)^{x} \\
&= \frac{(r+x-1)!}{x! (r-1)!} p^{r} (1-p)^{x} \quad (2)
\end{align}
$$
$(2)$式を元にvi)の導出結果の$x_6$に対応する確率変数が従う負の二項分布のパラメータを答えよ。

・解答
i)
確率関数$p(x)$は下記のように表すことができる。
$$
\large
\begin{align}
p(x) = \frac{\lambda^{x} e^{-\lambda}}{x!}
\end{align}
$$

ⅱ)
尤度$L(\lambda)$は標本が観測される同時確率に一致するので下記のように考えることができる。
$$
\large
\begin{align}
L(\lambda) &= \prod_{i=1}^{5} p(x_i) = \prod_{i=1}^{5} \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \\
&= \lambda^{\sum_{i=1}^{5} x_i} e^{-5 \lambda} \left( \prod_{i=1}^{5} x_i! \right)^{-1} \\
&= \lambda^{15} e^{-5 \lambda} \left( \prod_{i=1}^{5} x_i! \right)^{-1}
\end{align}
$$

ⅲ)
パラメータ$\lambda$の事前分布$\displaystyle \mathrm{Ga} \left( 3,\frac{1}{2} \right)$の確率密度関数$P(\lambda)$は下記のように表すことができる。
$$
\large
\begin{align}
P(\lambda) = \frac{2^{3}}{\Gamma(3)} \lambda^{3-1} e^{-2 \lambda}
\end{align}
$$

iv)
事後分布の確率密度関数を$P(\lambda|x_1,\cdots,x_5)$とおくと、$P(\lambda|x_1,\cdots,x_5)$は下記のように考えることができる。
$$
\large
\begin{align}
P(\lambda|x_1,\cdots,x_n) & \propto P(x_1,\cdots,x_5|\lambda)P(\lambda) \\
& \propto \lambda^{15} e^{-5 \lambda} \times \lambda^{3-1} e^{-2 \lambda} \\
&= \lambda^{18-1} e^{-7 \lambda}
\end{align}
$$

上記より、$\lambda$の事後分布はガンマ分布$\displaystyle \mathrm{Ga} \left( 18,\frac{1}{7} \right)$であると考えることができる。

v)
$P(\lambda|x_1,\cdots,x_n)$はガンマ分布$\displaystyle \mathrm{Ga} \left( 18,\frac{1}{7} \right)$の確率密度関数であるので下記のように表せる。
$$
\large
\begin{align}
P(\lambda|x_1,\cdots,x_n) = \frac{7^{18}}{\Gamma(18)} \lambda^{18-1} e^{-7 \lambda}
\end{align}
$$

vi)
$(1)$式を元に$P(x_{6}|x_1,\cdots,x_5)$は下記のように計算できる。
$$
\large
\begin{align}
P(x_{6}|x_1,\cdots,x_5) &= \int_{0}^{\infty} P(x_{6}|\lambda) P(\lambda|x_1,\cdots,x_5) d \lambda \quad (1) \\
&= \int_{0}^{\infty} \frac{\lambda^{x_6} e^{-\lambda}}{x_6!} \times \frac{7^{18}}{\Gamma(18)} \lambda^{18-1} e^{-7 \lambda} d \lambda \\
&= \frac{7^{18}}{x_6! \Gamma(18)} \int_{0}^{\infty} \lambda^{18+x_6-1} e^{-8 \lambda} d \lambda \\
&= \frac{7^{18}}{x_6! \Gamma(18)} \times \frac{\Gamma(18+x_6)}{8^{18+x_6}} \\
&= \frac{(18+x_6-1)!}{x_6! (18-1)!} \cdot \left( \frac{7}{8} \right)^{18} \cdot \left( \frac{1}{8} \right)^{x_6}
\end{align}
$$

vⅱ)
$(2)$式に対し、$\displaystyle r=18, x=x_6, p=\frac{7}{8}$で置き換えることでvi)の$P(x_{6}|x_1,\cdots,x_5)$の式が得られる。よって、$x_6$に対応する確率変数は負の二項分布$\displaystyle \mathrm{NB} \left( 18,\frac{7}{8} \right)$に従うと考えられる。

・解説
問題の作成にあたっては下記の問題の設定を主に用いました。

「統計学実践ワークブック」 演習問題etc Ch.31 「ベイズ法」

参考

• カテゴリ分布のパラメータを推論する（前半）（YouTube）
• カテゴリ分布のパラメータを推論する（後半）（YouTube）
  • カテゴリ分布（多項分布の特殊形）のパラメータのベイズ推論について解説