当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$2.9.3$節「$2$変量正規分布」の内容を元に$2$変量正規分布の数式とその解釈関して取りまとめました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
Contents
$2$変量正規分布の概要
概要
当記事では$2$つの確率変数$X \sim \mathcal{N}(\mu_x, \sigma_x^2), \, Y \sim \mathcal{N}(\mu_y, \sigma_y^2)$の相関係数を$\rho$とする場合の確率分布について取り扱います。
基本的に$2$級範囲では概要を抑えておくだけで良いと思われますが、必要な場合に詳しい式変形が確認できるように別途行った導出を参照しました。
必要な数学
式を確認するにあたって、展開・因数分解(factorization)の基本公式は抑えておくと良いと思います。
また、等高線を理解するにあたっては、固有値・固有ベクトルの理解が必須です。$2$級範囲では基本的に出題されませんので、理解は必須ではありません。
$2$変量正規分布
$2$変量正規分布の数式
$2$つの連続型確率変数$X \sim \mathcal{N}(\mu_x, \sigma_x^2), \, Y \sim \mathcal{N}(\mu_y, \sigma_y^2)$の相関係数を$\rho$、同時確率密度関数を$f(x,y)$とおくとき、$f(x,y)$は下記のように表すことができます。
$$
\large
\begin{align}
f(x,y) &= \frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}} \exp{ \left[ -\frac{q(x,y)}{2} \right] } \\
q(x,y) &= \frac{1}{1-\rho^2} \left[ \left( \frac{x-\mu_x}{\sigma_x} \right)^2 – 2 \rho \left( \frac{x-\mu_x}{\sigma_x} \right)\left( \frac{y-\mu_y}{\sigma_y} \right) + \left( \frac{y-\mu_y}{\sigma_y} \right)^2 \right]
\end{align}
$$
上記の式で表される$2$次元の確率分布を$2$変量正規分布($2$-variate normal distribution)といいます。ここで変量(variate)は確率変数を意味し、多変量解析は複数の確率変数を含む統計解析を表すことも合わせて抑えておくと良いです。
具体的なパラメータと$2$変量正規分布
$\mu_1=1, \mu_2=1, \sigma_x=1, \sigma_y=1, \rho=0.7$のとき、前項で確認を行なった確率密度関数$f(x,y)$は下記のように表すことができます。
$$
\large
\begin{align}
q(x,y) &= \frac{1}{1-\rho^2} \left[ \left( \frac{x-\mu_x}{\sigma_x} \right)^2 – 2 \rho \left( \frac{x-\mu_x}{\sigma_x} \right)\left( \frac{y-\mu_y}{\sigma_y} \right) + \left( \frac{y-\mu_y}{\sigma_y} \right)^2 \right] \\
&= \frac{1}{1-0.7^2} \left[ \left( \frac{x-1}{1} \right)^2 – 2 \cdot 0.7 \left( \frac{x-1}{1} \right)\left( \frac{y-1}{1} \right) + \left( \frac{y-1}{1} \right)^2 \right] \\
&= \frac{1}{0.51} \left[ (x-1)^2 – 1.4 (x-1)(y-1) + (y-1)^2 \right] \\
f(x,y) &= \frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}} \exp{ \left[ -\frac{q(x,y)}{2} \right] } \\
&= \frac{1}{2 \pi \cdot 1 \cdot 1 \sqrt{1-0.7^2}} \exp{ \left[ -\frac{(x-1)^2 – 1.4 (x-1)(y-1) + (y-1)^2}{2 \cdot 0.51} \right] } \\
&= \frac{1}{2 \sqrt{0.51} \pi} \exp{ \left[ -\frac{(x-1)^2 – 1.4 (x-1)(y-1) + (y-1)^2}{1.02} \right] }
\end{align}
$$
上記の$f(x,y)$等高線の$1$つは下記のように表すことができます。
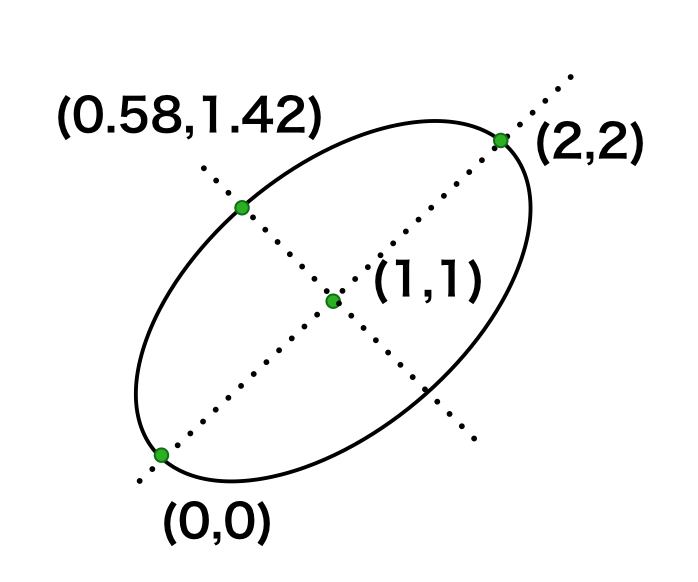
導出は$2$級範囲では必要ないので省略しましたが、詳しくは下記で取り扱いました。
$2$変量正規分布の条件付き分布・周辺分布
下記で詳しく取り扱いました。
