多次元正規分布の指数関数の内部の平方完成に着目することで、条件付き分布・周辺分布・予測分布などの様々な分布の導出が可能になる。一方で、周辺分布の計算などのように計算が複雑になる場合も多いので、当記事では多次元正規分布の平方完成に関連する分布について演習の作成を行った。
・多次元正規分布の確率密度関数の直感的な理解
https://www.hello-statisticians.com/explain-terms-cat/multi_norm_dist1.html
・$2$次元正規分布における条件付き確率分布・周辺分布の数式の導出
https://www.hello-statisticians.com/explain-terms-cat/multi_norm_dist3.html
・標準演習$100$選
https://www.hello-statisticians.com/practice_100
Contents
基本問題
$2$次元正規分布の条件付き確率
・問題
$$
\begin{align}
\mathbf{x} &= \left(\begin{array}{c} x_{1} \\ x_{2} \end{array} \right) \quad (1) \\
\mathbf{\mu} &= \left(\begin{array}{c} \mu_{1} \\ \mu_{2} \end{array} \right) \quad (2) \\
\mathbf{\Sigma} &= \left(\begin{array}{cc} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{array} \right) \quad (3)
\end{align}
$$
上記で定義した$\mathbf{x}, \mathbf{\mu}, \mathbf{\Sigma}$を元に、$2$次元正規分布$N(\mathbf{\mu}, \mathbf{\Sigma})$を仮定する。このとき、$2$変数$x_1, x_2$に関する$2$次元正規分布の条件付き確率分布を$1$次元の正規分布$N(\mu_{x_1|x_2}, \Sigma_{x_1|x_2})$で表すと考える。
ここで、$\mu_{x_1|x_2}, \Sigma_{x_1|x_2}$は下記のようになる。
$$
\begin{align}
\mu_{x_1|x_2} &= \mu_{1}+\frac{\sigma_{12}}{\sigma_{22}}(x_{2}-\mu_{2}) \quad (4) \\
\Sigma_{x_1|x_2} &= \sigma_{11} – \frac{\sigma_{12}^2}{\sigma_{22}} \quad (5)
\end{align}
$$
$\mu_{x_1|x_2}, \Sigma_{x_1|x_2}$の詳しい導出については下記で取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/multi_norm_dist3.html#i-2
ここまでの内容に基づいて、下記の問いに答えよ。
i) 下記のように分散共分散行列の$\mathbf{\Sigma}$が得られるとき、$\mu_{x_1|x_2}, \Sigma_{x_1|x_2}$に代入し、結果を計算せよ。
$$
\begin{align}
\mathbf{\Sigma} = \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align}
$$
ⅱ) 下記のように分散共分散行列の$\mathbf{\Sigma}$が得られるとき、i)と同様に代入を行い、$\Sigma_{x_1|x_2}$の値をi)と比較せよ。
$$
\begin{align}
\mathbf{\Sigma} = \left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)
\end{align}
$$
ⅲ) 下記のv)の結果を元に、ⅱ)の分散共分散行列を持つ$2$次元正規分布の確率密度関数に関して、確率密度に関する等高線を$1$つ用いて図示せよ。
https://www.hello-statisticians.com/practice/stat_practice3.html#i-6
iv) ⅲ)で行った描画を元にⅱ)で導出を行った$\mu_{x_1|x_2}$に関する考察を行え。
v) ⅲ)で行った描画を元に$(5)$式で表した$\Sigma_{x_1|x_2}$に関する考察を行え。
・解答
i) $\sigma_{11}=1, \sigma_{12}=0, \sigma_{21}=0, \sigma_{22}=1$を$(2)$式、$(3)$式に代入することで、下記のように$\mu_{x_1|x_2}, \Sigma_{x_1|x_2}$が得られる。
$$
\large
\begin{align}
\mu_{x_1|x_2} &= \mu_{1}+\frac{\sigma_{12}}{\sigma_{22}}(x_{2}-\mu_{2}) \\
&= \mu_{1} + \frac{0}{1}(x_{2}-\mu_{2}) \\
&= \mu_{1} \\
\Sigma_{x_1|x_2} &= \sigma_{11} – \frac{\sigma_{12}^2}{\sigma_{22}} \\
&= 1 – \frac{0^2}{1} \\
&= 1
\end{align}
$$
上記より、$x_1,x_2$の共分散が$0$の場合は条件付き分布$P(x_1|x_2)$は$N(\mu_{1}, \sigma_{11})$に従うことが確認できる。
ⅱ) $\sigma_{11}=1, \sigma_{12}=0.7, \sigma_{21}=0.7, \sigma_{22}=1$を$(2)$式、$(3)$式に代入することで、下記のように$\mu_{x_1|x_2}, \Sigma_{x_1|x_2}$が得られる。
$$
\large
\begin{align}
\mu_{x_1|x_2} &= \mu_{1}+\frac{\sigma_{12}}{\sigma_{22}}(x_{2}-\mu_{2}) \\
&= \mu_{1} + \frac{0.7}{1}(x_{2}-\mu_{2}) \\
&= \mu_{1} + 0.7(x_{2}-\mu_{2}) \\
\Sigma_{x_1|x_2} &= 1 – \frac{0.7^2}{1} \\
&= 1 – 0.49 \\
&= 0.51
\end{align}
$$
上記をi)の結果と比較するとき、分散が小さくなったことが確認できる。また、共分散の値が大きくなるにつれて、$\Sigma_{x_1|x_2}$が小さくなることも同時に確認できる。
ⅲ)
下記のように図示を行うことができる。
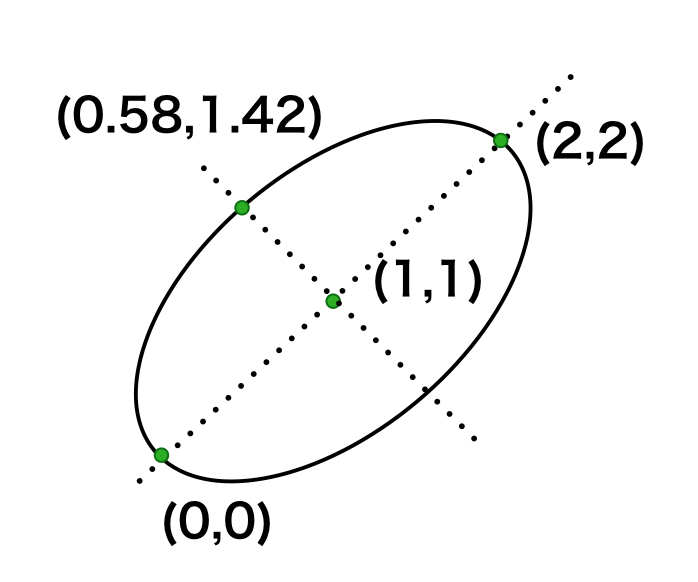
参照先のv)が$\mu_{1}=1, \mu_{2}=1$が前提だったので上記のように図示したが、$\mu_{1}, \mu_{2}$の値が変わっても単に平行移動を行うことで求めることができる。
iv)
$$
\large
\begin{align}
\mu_{x_1|x_2} = \mu_{1}+0.7(x_{2}-\mu_{2})
\end{align}
$$
ⅱ)で導出を行った上記を$x_{2}$に関して考えると、点$(\mu_{1},\mu_{2})$を通る傾き0.7の直線であることがわかる。同時に$x_{2} > \mu_{2}$の際に$\mu_{x_1|x_2}$が$\mu_{1}$より大きくなり、$x_{2} < \mu_{2}$の際に$\mu_{x_1|x_2}$が$\mu_{1}$よりも小さくなることも考えることができる。これをⅲ)で行った描画と見比べると、確率密度関数の等高線が右上と左下に向けて広がっていくことに対応することがわかる。
v)
$$
\large
\begin{align}
\Sigma_{x_1|x_2} &= \sigma_{11} – \frac{\sigma_{12}^2}{\sigma_{22}}
\end{align}
$$
$(5)$式は上記のように表されるが、共分散の絶対値が大きくなるにつれて条件付き分布の分散が小さくなることが確認できる。
このことをⅲ)の描画を元に考えると、共分散が大きくなるにつれて確率密度関数に基づく等高線が丸から楕円、直線に移行することに対応する。このように等高線が変化することで、共分散の絶対値が大きくなるにつれて条件付き分布の分散が小さくなることに対応すると考えることができる。
・解説
ここではそれぞれの変数の分散が$1$、共分散が$0.7$の$2$次元正規分布に関する取り扱いについて考えました。ⅱ)で導出した結果とⅲ)で行った描画を見比べることで、$2$次元正規分布に関する数式の理解がしやすいのではないかと思います。
