数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現を行います。当記事では統計的推測(statistical inference)の理解にあたって、区間推定や仮説検定のPythonでの実装を取り扱いました。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
Contents
基本事項の確認
区間推定
下記で詳しく取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/flow_chart_stat1.html
仮説検定
推測統計でよく用いるSciPyのメソッド
SciPyの使用にあたっては、scipy.stats.xxx.oooのように使用するメソッドの指定を行うが、xxxに確率分布、oooに行う処理を指定する。
推測統計ではxxxに対して主に下記などの確率分布の指定を行う。
norm: 正規分布t: $t$分布chi2: $\chi^2$分布
同様に推測統計ではoooに対して、主に下記の処理の指定を行う。
cdf: 統計量から有意水準・$P$値の計算ppf: 有意水準・$P$値から統計量の計算pdf: 統計量から確率密度関数の計算
特にcdfとppfは区間推定や検定で統計数値表の代わりに用いることができる。
以下、標準正規分布を例にcdf、ppf、pdfの概要の確認を行う。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
x = np.arange(-3.,3.01,0.01)
f_pdf = stats.norm.pdf(x)
F_cdf = stats.norm.cdf(x)
plt.plot(x,f_pdf,label="pdf")
plt.plot(x,F_cdf,label="cdf")
plt.legend()
plt.show()・実行結果
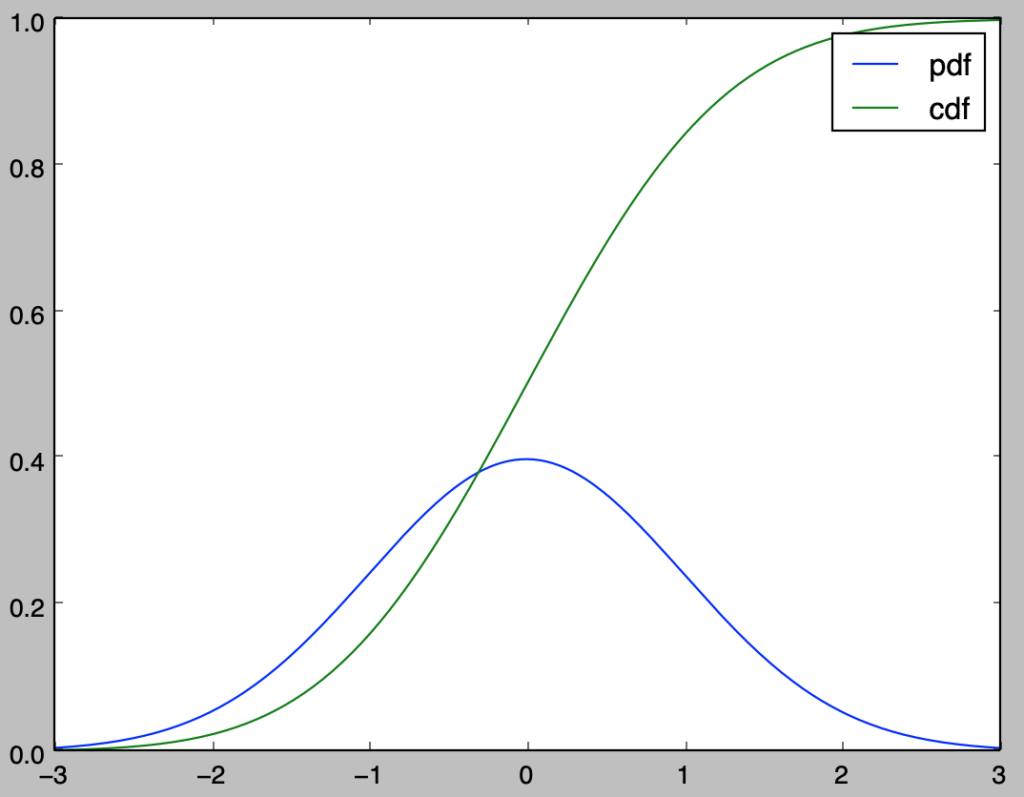
上記のようにcdf、pdfを用いることで累積分布関数と確率密度関数の描画を行うことができる。
次に、cdfとppfの対応に関して確認を行う。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
alpha = np.array([0.1, 0.05, 0.025, 0.01, 0.005])
x = np.arange(-3.,3.01,0.01)
F_cdf = stats.norm.cdf(x)
plt.plot(x,F_cdf,label="cdf")
for i in range(alpha.shape[0]):
print("alpha: {}, statistic_upper: {:.2f}".format(alpha[i], stats.norm.ppf(1.-alpha[i])))
x_upper = np.repeat(stats.norm.ppf(1.-alpha[i]), 100)
y = np.linspace(0,1.-alpha[i],100)
plt.plot(x_upper,y,label="alpha: {}".format(alpha[i]))
plt.legend(loc=2)
plt.show()・実行結果
alpha: 0.1, statistic_upper: 1.28
alpha: 0.05, statistic_upper: 1.64
alpha: 0.025, statistic_upper: 1.96
alpha: 0.01, statistic_upper: 2.33
alpha: 0.005, statistic_upper: 2.58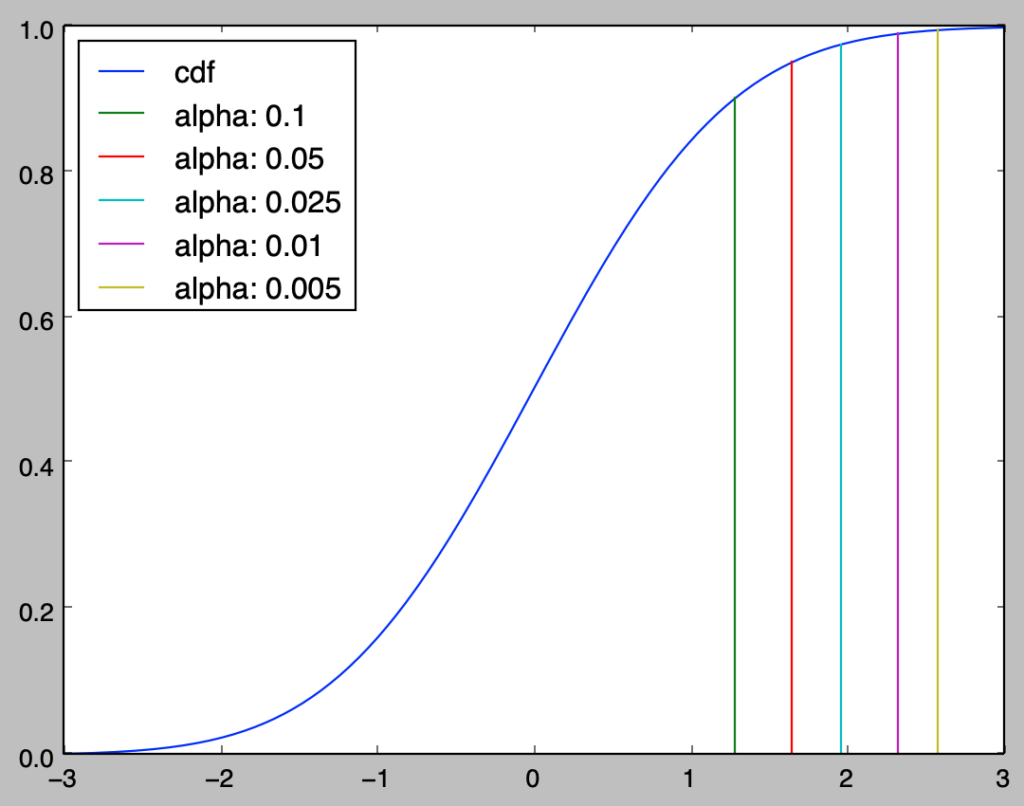
上記よりcdfとppfは逆関数であると考えることができる。それぞれの対応がわかりやすいように、下記では上図の編集を行った。
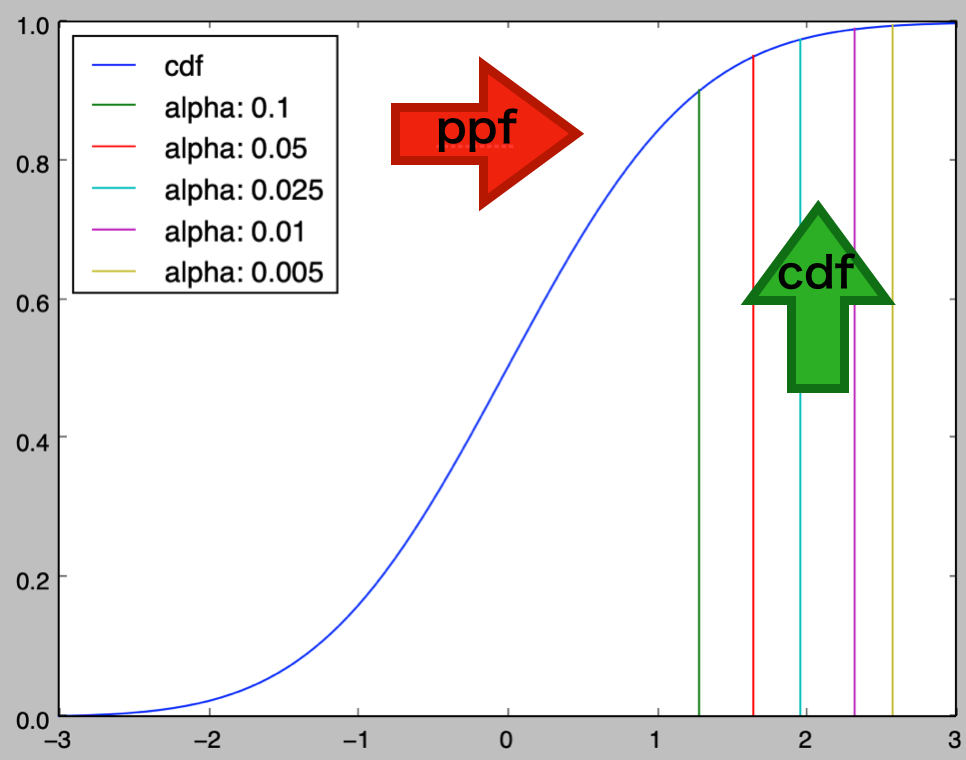
統計数値表とSciPyを用いた代用
scipy.statsのscipy.stats.norm、scipy.stats.t、scipy.stats.chi2を用いることで、統計的推測を行うことができる。特に区間推定や仮説検定でよく用いられる統計数値表が、累積分布関数に対応するscipy.stats.norm.cdfなどを活用することで作成できることは抑えておくと良い。
以下ではscipy.stats.norm.cdfやscipy.stats.norm.ppfなどを用いることで統計数値表を作成し概要の理解を行うことに加えて、SciPyで代用する際の用い方について確認を行う。
標準正規分布
統計数値表の作成
上側確率が$100 \alpha’$%となる点を$z_{\alpha=\alpha’}$とおくとき、$z_{\alpha=\alpha’}=0$から$0.01$刻みで該当する$\alpha’$の値を表形式で表したものが統計数値表である。以下、$500$個の値を$50$行$10$列に並べることで標準正規分布の統計数値表の作成を行う。
import numpy as np
from scipy import stats
z = np.arange(0., 5., 0.01).reshape([50,10])
table_norm = 1. - stats.norm.cdf(z)
print(table_norm)・実行結果
array([[ 5.00000000e-01, 4.96010644e-01, 4.92021686e-01,
4.88033527e-01, 4.84046563e-01, 4.80061194e-01,
4.76077817e-01, 4.72096830e-01, 4.68118628e-01,
4.64143607e-01],
[ 4.60172163e-01, 4.56204687e-01, 4.52241574e-01,
4.48283213e-01, 4.44329995e-01, 4.40382308e-01,
4.36440537e-01, 4.32505068e-01, 4.28576284e-01,
4.24654565e-01],
.....
[ 4.79183277e-07, 4.55381965e-07, 4.32721062e-07,
4.11148084e-07, 3.90612854e-07, 3.71067408e-07,
3.52465898e-07, 3.34764508e-07, 3.17921366e-07,
3.01896462e-07]])処理の理解にあたっては、上側確率であることから1. - stats.norm.cdf(z)のように$1$から引いたと考えると良い。
SciPyを用いた統計数値表の代用
・有意水準$\alpha$から標準化変量$Z$を導出
有意水準$\alpha$から標準化変量$Z$を導出する場合はscipy.stats.norm.ppfを用いればよい。
import numpy as np
from scipy import stats
alpha = np.array([0.1, 0.05, 0.025, 0.01, 0.005])
Z_Limit = stats.norm.ppf(1.-alpha)
print(Z_Limit)・実行結果
> print(Z_Limit)
array([ 1.28155157, 1.64485363, 1.95996398, 2.32634787, 2.5758293 ])・標準化変量$Z$から有意水準$\alpha$を導出
標準化変量$Z$から有意水準$\alpha$を導出する場合は、統計数値表の作成と同様にscipy.stats.norm.cdfを用いればよい。
import numpy as np
from scipy import stats
Z = np.array([0., 0.5, 1., 1.5, 2., 2.5, 3.])
alpha = 1.-stats.norm.cdf(Z)
print(alpha)・実行結果
> print(alpha)
[ 0.5 0.30853754 0.15865525 0.0668072 0.02275013 0.00620967
0.0013499 ]$t$分布
統計数値表の作成
自由度が$\nu$の$t$分布$t(\nu)$に関して、上側確率が$100 \alpha’$%となる点を$t_{\alpha=\alpha’}(\nu)$とおくとき、$\alpha’=\{0.25, 0.20, 0.15, 0.10, 0.05, 0.025, 0.01, 0.005, 0.001\}$に対して、$\nu$を変化させたときに$t_{\alpha=\alpha’}(\nu)$の値をまとめたものが$t$分布の統計数値表である。以下、それぞれの有意水準と自由度に対して$t$分布の統計数値表の作成を行う。
import numpy as np
from scipy import stats
alpha = np.array([0.25, 0.20, 0.15, 0.10, 0.05, 0.025, 0.01, 0.005, 0.0005])
nu = np.arange(1,56,1)
nu[50:] = np.array([60., 80., 120., 240., 100000])
table_t = np.zeros([nu.shape[0],alpha.shape[0]])
for i in range(nu.shape[0]):
table_t[i,:] = stats.t.ppf(1.-alpha,nu[i])
print(table_t)・実行結果
[[ 1. 1.37638192 1.96261051 3.07768354 6.31375151
12.70620474 31.82051595 63.65674116 636.61924943]
[ 0.81649658 1.06066017 1.38620656 1.88561808 2.91998558
4.30265273 6.96455672 9.9248432 31.59905458]
[ 0.76489233 0.97847231 1.2497781 1.63774436 2.35336343
3.18244631 4.54070286 5.8409093 12.92397864]
.....
[ 0.67551336 0.84312147 1.0386776 1.28508893 1.65122739
1.96989764 2.34198547 2.59646918 3.33152484]
[ 0.6744922 0.84162483 1.03643876 1.28156003 1.64486886
1.95998771 2.32638517 2.57587847 3.29062403]]処理の理解にあたっては、上側確率であることから1. - alphaのように$1$から引いたと考えると良い。
SciPyを用いた統計数値表の代用
・有意水準$\alpha$からパーセント点$t_{\alpha=\alpha’}(\nu)$を導出
有意水準$\alpha$からパーセント点$t_{\alpha=\alpha’}(\nu)$を導出する場合は統計数値表の作成と同様にscipy.stats.t.ppfを用いればよい。
import numpy as np
from scipy import stats
alpha = np.array([0.1, 0.05, 0.025, 0.01, 0.005])
Z_Limit = stats.norm.ppf(1.-alpha)
t_Limit_20 = stats.t.ppf(1.-alpha, 20)
t_Limit_100 = stats.t.ppf(1.-alpha, 100)
print(Z_Limit)
print(t_Limit_20)
print(t_Limit_100)・実行結果
> print(Z_Limit)
[ 1.28155157 1.64485363 1.95996398 2.32634787 2.5758293 ]
> print(t_Limit_20)
[ 1.32534071 1.72471824 2.08596345 2.527977 2.84533971]
> print(t_Limit_100)
[ 1.29007476 1.66023433 1.98397152 2.36421737 2.62589052]上記より、$t$分布の棄却点は標準正規分布の棄却点より絶対値が大きくなることが確認できる。また、t_Limit_20とt_Limit_100の比較により、自由度が大きくなるにつれて$t$分布が標準正規分布に近づくことも確認できる。
・パーセント点$t_{\alpha=\alpha’}(\nu)$から有意水準$\alpha$を導出
統計量$t$から有意水準$\alpha$を導出する場合は、scipy.stats.t.cdfを用いればよい。
import numpy as np
from scipy import stats
t = np.array([0., 0.5, 1., 1.5, 2., 2.5, 3.])
alpha_20 = 1.-stats.t.cdf(t,20)
alpha_100 = 1.-stats.t.cdf(t,100)
print(alpha_20)
print(alpha_100)・実行結果
> print(alpha_20)
[ 0.5 0.31126592 0.16462829 0.07461789 0.02963277 0.01061677
0.00353795]
> print(alpha_100)
[ 0.5 0.30908678 0.15986208 0.06838253 0.02410609 0.00702289
0.00170396]$\chi^2$分布
統計数値表の作成
自由度が$\nu$の$\chi^2$分布$\chi^2(\nu)$に関して、上側確率が$100 \alpha’$%となる点を$\chi^2_{\alpha=\alpha’}(\nu)$とおくとき、$\alpha’=\{0.995, 0.990, 0.975, 0.950, 0.900, 0.800, …, 0.100, 0.050, 0.025, 0.010, 0.005, 0.001\}$に対して、$\nu$を変化させたときに$t_{\alpha=\alpha’}(\nu)$の値をまとめたものが「基礎統計学Ⅰ」における$\chi^2$分布の統計数値表である。以下、それぞれの有意水準と自由度に対して$\chi^2$分布の統計数値表の作成を行う。
import numpy as np
from scipy import stats
alpha = np.array([0.995, 0.990, 0.975, 0.95, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.05, 0.025, 0.01, 0.005, 0.001])
nu = np.arange(1,62,1)
nu[50:] = np.array([60., 70., 80., 90., 100., 120., 140., 160., 180., 200., 240.])
table_chi2 = np.zeros([nu.shape[0],alpha.shape[0]])
for i in range(nu.shape[0]):
table_chi2[i,:] = stats.chi2.ppf(1.-alpha,nu[i])
print(table_chi2)・実行結果
[[ 3.92704222e-05 1.57087858e-04 9.82069117e-04 ..., 6.63489660e+00
7.87943858e+00 1.08275662e+01]
[ 1.00250836e-02 2.01006717e-02 5.06356160e-02 ..., 9.21034037e+00
1.05966347e+01 1.38155106e+01]
[ 7.17217746e-02 1.14831802e-01 2.15795283e-01 ..., 1.13448667e+01
1.28381565e+01 1.62662362e+01]
.....
[ 1.52240992e+02 1.56431966e+02 1.62727983e+02 ..., 2.49445123e+02
2.55264155e+02 2.67540528e+02]
[ 1.87324255e+02 1.91989896e+02 1.98983851e+02 ..., 2.93888101e+02
3.00182237e+02 3.13436899e+02]]SciPyを用いた統計数値表の代用
・有意水準$\alpha$からパーセント点$\chi^2_{\alpha=\alpha’}(\nu)$を導出
有意水準$\alpha$からパーセント点$\chi^2_{\alpha=\alpha’}(\nu)$を導出する場合は統計数値表の作成と同様にscipy.stats.chi2.ppfを用いればよい。
import numpy as np
from scipy import stats
alpha = np.array([0.975, 0.95, 0.1, 0.05, 0.025])
chi2_Limit_1 = stats.chi2.ppf(1.-alpha, 1)
chi2_Limit_10 = stats.chi2.ppf(1.-alpha, 10)
chi2_Limit_100 = stats.chi2.ppf(1.-alpha, 100)
print(chi2_Limit_1)
print(chi2_Limit_10)
print(chi2_Limit_100)・実行結果
print(chi2_Limit_1)
[ 9.82069117e-04 3.93214000e-03 2.70554345e+00 3.84145882e+00
5.02388619e+00]
print(chi2_Limit_10)
[ 3.24697278 3.94029914 15.98717917 18.30703805 20.48317735]
print(chi2_Limit_100)
[ 74.22192747 77.92946517 118.49800381 124.3421134 129.56119719]・パーセント点$\chi^2_{\alpha=\alpha’}(\nu)$から有意水準$\alpha$を導出
統計量$\chi^2$から有意水準$\alpha$を導出する場合は、scipy.stats.chi2.cdfを用いればよい。
import numpy as np
from scipy import stats
chi2 = np.array([2., 5., 10., 15., 20., 50., 100.])
alpha_1 = 1.-stats.chi2.cdf(chi2,1)
alpha_5 = 1.-stats.chi2.cdf(chi2,5)
alpha_10 = 1.-stats.chi2.cdf(chi2,10)
alpha_20 = 1.-stats.chi2.cdf(chi2,20)
alpha_100 = 1.-stats.chi2.cdf(chi2,100)
print(alpha_1)
print(alpha_5)
print(alpha_10)
print(alpha_20)
print(alpha_100)・実行結果
> print(alpha_1)
[ 1.57299207e-01 2.53473187e-02 1.56540226e-03 1.07511177e-04
7.74421643e-06 1.53743684e-12 0.00000000e+00]
> print(alpha_5)
[ 8.49145036e-01 4.15880187e-01 7.52352461e-02 1.03623379e-02
1.24973056e-03 1.38579737e-09 0.00000000e+00]
> print(alpha_10)
[ 9.96340153e-01 8.91178019e-01 4.40493285e-01 1.32061856e-01
2.92526881e-02 2.66908343e-07 0.00000000e+00]
> print(alpha_20)
[ 9.99999889e-01 9.99722648e-01 9.68171943e-01 7.76407613e-01
4.57929714e-01 2.21476638e-04 1.25965904e-12]
> print(alpha_100)
[ 1. 1. 1. 1. 1. 0.99999305
0.48119168]区間推定・仮説検定
母分散既知の場合の母平均
区間推定
$$
\large
\begin{align}
\bar{x}-1.96\frac{\sigma}{\sqrt{n}} \leq &\mu \leq \bar{x}+1.96\frac{\sigma}{\sqrt{n}}
\end{align}
$$
母平均の$95$%区間推定は上記のように表される。以下、上記を元に具体的な例に対して計算を行う。
import numpy as np
from scipy import stats
sigma = 1.
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
ave_x = np.mean(x)
Lower_mu = ave_x + stats.norm.ppf(0.025)*sigma/np.sqrt(x.shape[0])
Upper_mu = ave_x + stats.norm.ppf(0.975)*sigma/np.sqrt(x.shape[0])
print("Estimated mu-interval: [{:.3f}, {:.3f}]".format(Lower_mu, Upper_mu))・実行結果
> print("Estimated mu-interval: [{:.3f}, {:.3f}]".format(Lower_mu, Upper_mu))
Estimated mu-interval: [0.203, 1.957]以下、$\sigma$の値を変化させた際の区間推定の結果の確認を行う。
import numpy as np
from scipy import stats
sigma = np.array([0.1, 0.25, 0.5, 1., 2.])
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
ave_x = np.mean(x)
Lower_mu = ave_x + stats.norm.ppf(0.025)*sigma/np.sqrt(x.shape[0])
Upper_mu = ave_x + stats.norm.ppf(0.975)*sigma/np.sqrt(x.shape[0])
for i in range(sigma.shape[0]):
print("Estimated mu-interval: [{:.3f}, {:.3f}]".format(Lower_mu[i], Upper_mu[i]))・実行結果
Estimated mu-interval: [0.992, 1.168]
Estimated mu-interval: [0.861, 1.299]
Estimated mu-interval: [0.642, 1.518]
Estimated mu-interval: [0.203, 1.957]
Estimated mu-interval: [-0.673, 2.833]Lower_muとUpper_muの計算にあたって、それぞれ0.025と0.975を引数に設定したが、これは上側確率を$\alpha’$とおく際の$1-\alpha’$に対応し、このように考えると少々わかりにくい。そのため、標準正規分布の累積分布関数の値から変数の値を計算すると考える方が良い。
これらの違いは元々が「統計数値表」に基づいて考えていた一方で、SciPyなどで実装を行う際には「数値表」が必要ないことからより関数的な表し方に変わったのではないかと考えられる。
SciPyでの表し方がより自然に思われるので、表よりもSciPyなどを用いた形式で理解する方がわかりやすいかもしれない。
仮説検定① 〜norm.ppfと区間推定の活用〜
前項のxとave_xに対し、帰無仮説を$H_0: \mu=0$と設定し、上側確率$\alpha’=\{0.05, 0.025, 0.005\}$を用いた仮説検定を行う。
$$
\large
\begin{align}
z_{\alpha=1-\alpha’} \leq &\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \leq z_{\alpha=\alpha’} \\
-z_{\alpha=\alpha’} \leq &\frac{\sqrt{n}}{\sigma}\bar{x} \leq z_{\alpha=\alpha’}
\end{align}
$$
ここでの検定統計量の$\displaystyle Z = \frac{\sqrt{n}}{\sigma}\bar{x}$に関して上記が成立しなければ$H_0$を棄却し、対立仮説の$H_1: \mu \neq 0$を採択する。
import numpy as np
from scipy import stats
alpha = np.array([0.05, 0.025, 0.005])
sigma = 1.
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
Z_observed = np.sqrt(x.shape[0])*np.mean(x)/sigma
Lower_Z = -stats.norm.ppf(1.-alpha)*sigma
Upper_Z = stats.norm.ppf(1.-alpha)*sigma
for i in range(alpha.shape[0]):
if Z_observed > Upper_Z[i] or Z_observed < Lower_Z[i]:
print("Z: {:.3f}. If alpha: {} -> Upper_Z: {:.2f}, reject H_0: mu=0. ".format(Z_observed, alpha[i], Upper_Z[i]))
else:
print("Z: {:.3f}. If alpha: {} -> Upper_Z: {:.2f}, accept H_0: mu=0. ".format(Z_observed, alpha[i], Upper_Z[i]))・実行結果
Z: 2.415. If alpha: 0.05 -> Upper_Z: 1.64, reject H_0: mu=0.
Z: 2.415. If alpha: 0.025 -> Upper_Z: 1.96, reject H_0: mu=0.
Z: 2.415. If alpha: 0.005 -> Upper_Z: 2.58, accept H_0: mu=0.上記より、上側確率を小さくするにつれて棄却されにくいことが確認できる。
仮説検定② 〜norm.cdfと$P$値の活用〜
前項の「仮説検定①」では区間推定の結果と$Z$の値を元に検定を行なったが、$Z$の値に対してnorm.cdfを用いることで$P$値を計算し、検定を行うこともできる。
import numpy as np
from scipy import stats
alpha = np.array([0.05, 0.025, 0.005])
sigma = 1.
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
Z_observed = np.sqrt(x.shape[0])*np.mean(x)/sigma
P_value = 1.-stats.norm.cdf(Z_observed)
for i in range(alpha.shape[0]):
if P_value > 1.-alpha[i] or P_value < alpha[i]:
print("Z: {:.3f}, P_value: {:.3f}. If alpha: {}, reject H_0: mu=0. ".format(Z_observed, P_value, alpha[i]))
else:
print("Z: {:.3f}, P_value: {:.3f}. If alpha: {}, accept H_0: mu=0. ".format(Z_observed, P_value, alpha[i]))・実行結果
Z: 2.415, P_value: 0.008. If alpha: 0.05, reject H_0: mu=0.
Z: 2.415, P_value: 0.008. If alpha: 0.025, reject H_0: mu=0.
Z: 2.415, P_value: 0.008. If alpha: 0.005, accept H_0: mu=0. 仮説検定は②で取り扱った「$P$値の活用」を用いる方が「ノンパラメトリック法」と同様に取り扱うことができるなど、わかりやすい。また、この際にppfとcdfの図を元に下記のように考えることもできる。
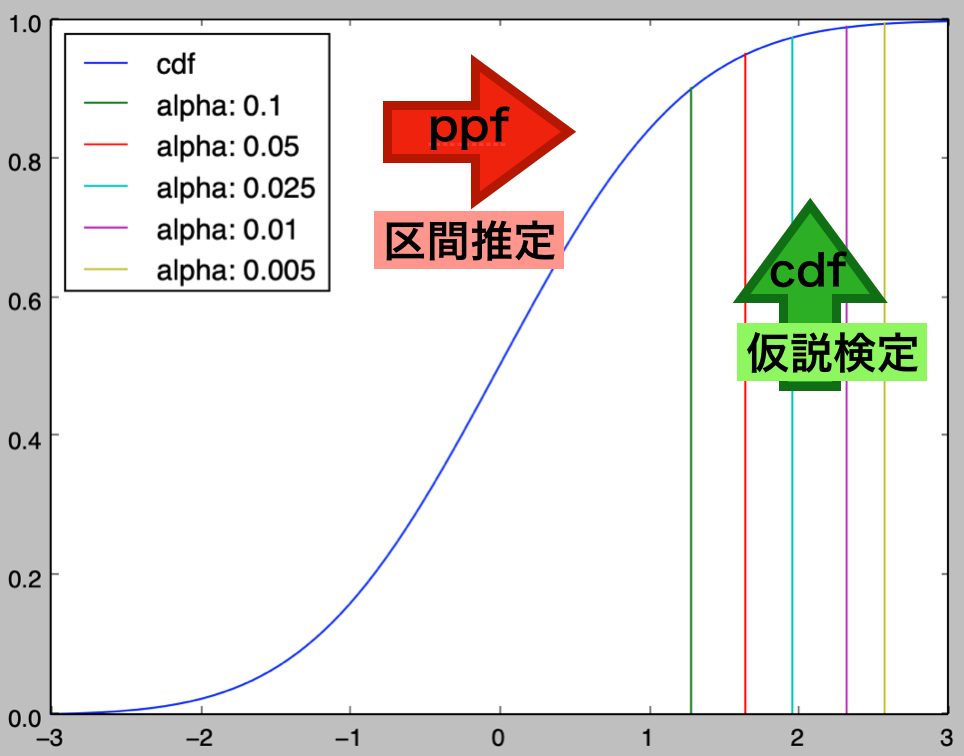
母分散未知の場合の母平均
区間推定
$$
\large
\begin{align}
\bar{x}-t_{\alpha=0.025}(n-1) \frac{s}{\sqrt{n}} \leq &\mu \leq \bar{x}+t_{\alpha=0.025}(n-1) \frac{s}{\sqrt{n}} \\
s = \frac{1}{n-1} & \sum_{i=1}^{n} (x_i-\bar{x})^2
\end{align}
$$
母分散が未知の際の母平均の$95$%区間推定は上記のように表される。以下、上記を元に具体的な例に対して計算を行う。
import numpy as np
from scipy import stats
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
ave_x = np.mean(x)
s = np.sqrt(np.sum((x-ave_x)**2/(x.shape[0]-1)))
Lower_mu = ave_x - stats.t.ppf(1-0.025, x.shape[0]-1)*s/np.sqrt(x.shape[0])
Upper_mu = ave_x + stats.t.ppf(1-0.025, x.shape[0]-1)*s/np.sqrt(x.shape[0])
print("s: {:.2f}".format(s))
print("Estimated mu-interval: [{:.3f}, {:.3f}]".format(Lower_mu, Upper_mu))・実行結果
> print("s: {:.2f}".format(s))
s: 0.30
> print("Estimated mu-interval: [{:.3f}, {:.3f}]".format(Lower_mu, Upper_mu))
Estimated mu-interval: [0.703, 1.457]母分散既知の場合と同様の事例を用いたが、$s=0.3$の周辺の$\sigma=0.25$の際の区間が[0.861, 1.299]、$\sigma=0.5$の際の区間が[0.642, 1.518]であったので、概ね同様の結果が得られていることが確認できる。
仮説検定
前項のxとave_xに対し、帰無仮説を$H_0: \mu_0=0.95$と設定し、上側確率$\alpha’=\{0.05, 0.025, 0.005\}$を用いた仮説検定を行う。
$$
\large
\begin{align}
t_{\alpha=1-\alpha’}(n-1) \leq &\frac{\bar{x}-\mu_0}{s/\sqrt{n}} \leq t_{\alpha=\alpha’}(n-1) \\
-t_{\alpha=\alpha’}(n-1) \leq &\frac{\sqrt{n}}{s} (\bar{x}-0.95) \leq t_{\alpha=\alpha’}(n-1)
\end{align}
$$
ここでの検定統計量の$\displaystyle t = \frac{\sqrt{n}}{s} (\bar{x}-\mu_0)$に関して上記が成立しなければ$H_0$を棄却し、対立仮説の$H_1: \mu_0 \neq 0.95$を採択する。
import numpy as np
from scipy import stats
mu_0 = 0.95
alpha = np.array([0.05, 0.025, 0.005])
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
ave_x = np.mean(x)
s = np.sqrt(np.sum((x-ave_x)**2/(x.shape[0]-1)))
t_observed = np.sqrt(x.shape[0])*(ave_x-mu_0)/s
Lower_t = -stats.t.ppf(1.-alpha, x.shape[0])*s
Upper_t = stats.t.ppf(1.-alpha, x.shape[0])*s
for i in range(alpha.shape[0]):
if t_observed > Upper_t[i] or t_observed < Lower_t[i]:
print("t: {:.3f}. If alpha: {}, reject H_0: mu=0. ".format(t_observed, alpha[i]))
else:
print("t: {:.3f}. If alpha: {}, accept H_0: mu=0. ".format(t_observed, alpha[i]))
print(Lower_t)
print(Upper_t)・実行結果
t: 0.958. If alpha: 0.05, reject H_0: mu=0.
t: 0.958. If alpha: 0.025, reject H_0: mu=0.
t: 0.958. If alpha: 0.005, accept H_0: mu=0.
> print(Lower_t)
[-0.61119443 -0.77969608 -1.22300952]
> print(Upper_t)
[ 0.61119443 0.77969608 1.22300952]上記より、上側確率を小さくするにつれて棄却されにくいことが確認できる。
母分散
区間推定
$$
\large
\begin{align}
\frac{(n-1)s^2}{\chi_{\alpha=0.025}^2(n-1)} \leq & \sigma^2 \leq \frac{(n-1)s^2}{\chi_{\alpha=0.975}^2(n-1)} \\
s = \frac{1}{n-1} & \sum_{i=1}^{n} (x_i-\bar{x})^2
\end{align}
$$
母分散の$95$%区間推定は上記のように表される。以下、上記を元に具体的な例に対して計算を行う。
import numpy as np
from scipy import stats
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1])
ave_x = np.mean(x)
s = np.sqrt(np.sum((x-ave_x)**2/(x.shape[0]-1)))
Lower_sigma2 = (x.shape[0]-1)*s**2/stats.chi2.ppf(1.-0.025, x.shape[0]-1)
Upper_sigma2 = (x.shape[0]-1)*s**2/stats.chi2.ppf(1.-0.975, x.shape[0]-1)
print("s^2: {:.2f}".format(s**2))
print("Estimated sigma2s-interval: [{:.3f}, {:.3f}]".format(Lower_sigma2, Upper_sigma2))・実行結果
> print("s^2: {:.2f}".format(s**2))
s^2: 0.09
> print("Estimated sigma2s-interval: [{:.3f}, {:.3f}]".format(Lower_sigma2, Upper_sigma2))
Estimated sigma2s-interval: [0.033, 0.760]以下、サンプルを増やした際に$95$%区間はどのように変化するかに関して確認を行う。
import numpy as np
from scipy import stats
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1, 0.5, 1.0, 1.3, 0.9, 1.2])
ave_x = np.mean(x)
s = np.sqrt(np.sum((x-ave_x)**2/(x.shape[0]-1)))
Lower_sigma2 = (x.shape[0]-1)*s**2/stats.chi2.ppf(1.-0.025, x.shape[0]-1)
Upper_sigma2 = (x.shape[0]-1)*s**2/stats.chi2.ppf(1.-0.975, x.shape[0]-1)
print("s^2: {:.2f}".format(s**2))
print("Estimated sigma2s-interval: [{:.3f}, {:.3f}]".format(Lower_sigma2, Upper_sigma2))・実行結果
> print("s^2: {:.2f}".format(s**2))
s^2: 0.09
> print("Estimated sigma2s-interval: [{:.3f}, {:.3f}]".format(Lower_sigma2, Upper_sigma2))
Estimated sigma2s-interval: [0.041, 0.289]上記よりサンプルを増やすと$\sigma^2$の$95$%区間が小さくなることが確認できる。
仮説検定
前項のxに対し、帰無仮説を$H_0: \sigma_0^2=0.3$と設定し、上側確率$\alpha’=\{0.05, 0.025, 0.005\}$を用いた仮説検定を行う。
$$
\large
\begin{align}
\chi_{\alpha=0.975}(n-1) \leq & \frac{(n-1)s^2}{\sigma_0^2} \leq \chi_{\alpha=0.025}(n-1) \\
s = \frac{1}{n-1} & \sum_{i=1}^{n} (x_i-\bar{x})^2
\end{align}
$$
ここでの検定統計量の$\displaystyle \chi^2 = \frac{(n-1)s^2}{\sigma_0^2}$に関して上記が成立しなければ$H_0$を棄却し、対立仮説の$H_1: \sigma^2 \neq 0.3$を採択する。
import numpy as np
from scipy import stats
sigma2_0 = 0.3
alpha = np.array([0.05, 0.025, 0.005])
x = np.array([1.2, 1.5, 0.9, 0.7, 1.1, 0.5, 1.0, 1.3, 0.9, 1.2])
ave_x = np.mean(x)
s = np.sqrt(np.sum((x-ave_x)**2/(x.shape[0]-1)))
chi2_observed = (x.shape[0]-1)*s**2/sigma2_0
Lower_chi2 = stats.chi2.ppf(alpha, x.shape[0]-1)
Upper_chi2 = stats.chi2.ppf(1.-alpha, x.shape[0]-1)
for i in range(alpha.shape[0]):
if chi2_observed > Upper_chi2[i] or chi2_observed < Lower_chi2[i]:
print("chi2: {:.3f}. If alpha: {}, reject H_0: sigma^2=0.3. ".format(chi2_observed, alpha[i]))
else:
print("chi2: {:.3f}. If alpha: {}, accept H_0: sigma^2=0.3. ".format(chi2_observed, alpha[i]))
print(Lower_chi2)
print(Upper_chi2)・実行結果
chi2: 2.603. If alpha: 0.05, reject H_0: sigma^2=0.3.
chi2: 2.603. If alpha: 0.025, reject H_0: sigma^2=0.3.
chi2: 2.603. If alpha: 0.005, accept H_0: sigma^2=0.3.
> print(Lower_t)
[ 3.32511284 2.7003895 1.7349329 ]
> print(Upper_t)
[ 16.9189776 19.0227678 23.58935078]上記より、上側確率を小さくするにつれて棄却されにくいことが確認できる。
