多変数の凸関数の制約なし最適化問題を取り扱うにあたっては多変数関数の勾配(gradient)やヘッセ行列(hessian matrix)を用いることで$1$次・$2$次の最適性条件を表すことができます。当記事ではそれぞれの式の表記や簡単な導出などの取りまとめを行いました。
「数理計画入門(朝倉書店)」の$4.3$節の「制約なし問題の最適性条件」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
前提の確認
問題設定
多変数関数$f(\mathbf{x})=f(x_1,\cdots,x_n)$について勾配$\nabla f(\mathbf{x})$とヘッセ行列$\nabla^2 f(\mathbf{x})$を下記のように定義する。
$$
\large
\begin{align}
\nabla f(\mathbf{x}) &= \left( \begin{array}{c} \displaystyle \frac{\partial f(\mathbf{x})}{\partial x_1} \\ \vdots \\ \displaystyle \frac{\partial f(\mathbf{x})}{\partial x_n} \end{array} \right) \\
\nabla^2 f(\mathbf{x}) &= \left( \begin{array}{c} \displaystyle \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \cdots & \displaystyle \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_n} \\ \vdots & \ddots & \vdots \\ \displaystyle \frac{\partial^2 f(\mathbf{x})}{\partial x_n \partial x_1} & \cdots & \displaystyle \frac{\partial^2 f(\mathbf{x})}{\partial x_n^2} \end{array} \right)
\end{align}
$$
ここで上記の「多変数関数$f(\mathbf{x})=f(x_1,\cdots,x_n)$の最小化」を「制約なし最適化問題」と見なし、以下局所最適解$\mathbf{x}^{*}$に関して成立する最適性条件について確認を行う。
凸関数
関数$f$が下に凸の凸関数であるとき下記が成立する。
$$
\large
\begin{align}
\mathbf{x}, \mathbf{y} \in \mathbb{R}, \, 0 \leq \alpha \leq 1 \, \implies \, f(\alpha \mathbf{x} + (1-\alpha) \mathbf{y}) \leq \alpha f(\mathbf{x}) + (1-\alpha) f(\mathbf{y})
\end{align}
$$
$f(x) = x^2$のような二次関数のようなイメージで理解すると良く、たとえば$x=0, y=2, \alpha=0.5$のとき$f(\alpha x + (1-\alpha) y), \alpha f(x) + (1-\alpha) f(y)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
f(\alpha x + (1-\alpha) y) &= f(0.5 \cdot 0 + (1 – 0.5) \cdot 2) \\
&= f(1) \\
&= 1^2 = 1 \\
\alpha f(x) + (1-\alpha) f(y) &= 0.5 f(0) + (1 – 0.5) f(2) \\
&= 0.5 \cdot 0^2 + 0.5 \cdot 2^2 \\
&= 2
\end{align}
$$
上記より$f(\alpha x + (1-\alpha) y) \leq \alpha f(x) + (1-\alpha) f(y)$が$x=0, y=2, \alpha=0.5$で成立することが確認できる。
上記の例は下記を実行することで図示できる。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0., 2.01, 0.01)
f_x = x**2
f_line = 2*x
plt.plot(x, f_x, color="limegreen", label="f(x)=x^2")
plt.plot(x, f_line, color="orange", label="chord")
plt.scatter(0.5*0+0.5*2., (0.5*0+0.5*2.)**2, color="green")
plt.scatter(0.5*0+0.5*2., 0.5*0**2+0.5*2.**2, color="red")
plt.legend()
plt.show()・実行結果
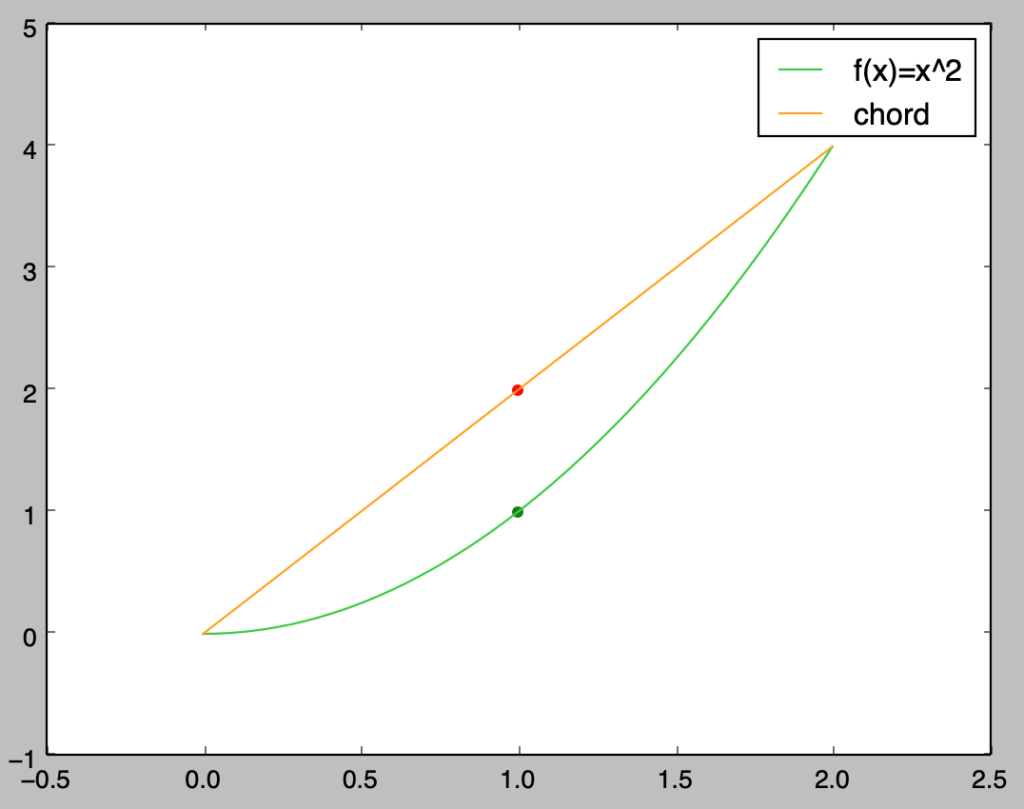
上図のように下に凸の凸関数の数式は「関数の上に弦が描画できる」と解釈することもできる。
最適性条件
最適性の1次の必要条件
$$
\large
\begin{align}
\nabla f(\mathbf{x}^{*}) &= \mathbf{0} \\
\left( \begin{array}{c} \displaystyle \frac{\partial f(\mathbf{x})}{\partial x_1} \\ \vdots \\ \displaystyle \frac{\partial f(\mathbf{x})}{\partial x_n} \end{array} \middle) \right|_{x_1=x_1^{*}, \cdots , x_n=x_n^{*}} &= \left( \begin{array}{c} 0 \\ \vdots \\ 0 \end{array} \right)
\end{align}
$$
最適性の$1$必要条件は上記のように表される。上記の式は「関数の最大値・最小値では各方向の勾配が$0$」であることに対応し、直感的には「山の頂上は平らである」と解釈すれば良い。
最適性の2次の必要条件
「ヘッセ行列$\nabla^2 f(\mathbf{x}^{*})$が半正定値行列」が$\mathbf{x}^{*}$が局所最適解である必要条件である。
最適性の2次の十分条件
$\mathbf{x}=\mathbf{x}^{*}$で「①勾配$\nabla f(\mathbf{x}^{*})$が$0$ベクトル」、「②ヘッセ行列$\nabla^2 f(\mathbf{x}^{*})$が正定値行列」であることが$\mathbf{x}^{*}$が局所最適解である十分条件である。このことを以下に示す。
目的関数$f$は最適解$\mathbf{x}^{*}$の周辺で下記のように表せる。
$$
\large
\begin{align}
f(\mathbf{x}^{*} + \alpha \mathbf{d}) = f(\mathbf{x}^{*}) + \alpha \nabla f(\mathbf{x}^{*})^{\mathrm{T}} \mathbf{d} + \frac{\alpha^2}{2} \mathbf{d}^{\mathrm{T}} \nabla^2 f(\mathbf{x}^{*}) \mathbf{d} + \mathcal{o}(||\mathbf{d}||^2)
\end{align}
$$
ここで$\nabla^2 f(\mathbf{x}^{*})$が正定値行列であれば、$\alpha$が十分小さいとき下記が成立する。
$$
\large
\begin{align}
\frac{\alpha^2}{2} \mathbf{d}^{\mathrm{T}} \nabla^2 f(\mathbf{x}^{}) \mathbf{d} + \mathcal{o}(||\mathbf{d}||^2) > 0
\end{align}
$$
よって、「①勾配$\nabla f(\mathbf{x}^{*})$が$0$ベクトル」、「②ヘッセ行列$\nabla^2 f(\mathbf{x}^{*})$が正定値行列」のとき下記が成立する。
$$
\large
\begin{align}
f(\mathbf{x}^{*} + \alpha \mathbf{d}) – f(\mathbf{x}^{*}) &= \alpha \nabla f(\mathbf{x}^{*})^{\mathrm{T}} \mathbf{d} + \frac{\alpha^2}{2} \mathbf{d}^{\mathrm{T}} \nabla^2 f(\mathbf{x}^{*}) \mathbf{d} + \mathcal{o}(||\mathbf{d}||^2) > 0 \\
f(\mathbf{x}^{*} + \alpha \mathbf{d}) – f(\mathbf{x}^{*}) & > 0 \\
f(\mathbf{x}^{*} + \alpha \mathbf{d}) & > f(\mathbf{x}^{*})
\end{align}
$$
上記より、「①勾配$\nabla f(\mathbf{x}^{*})$が$0$ベクトル」、「②ヘッセ行列$\nabla^2 f(\mathbf{x}^{*})$が正定値行列」が$\mathbf{x}^{*}$が最適解であることの十分条件であることが確認できる。
