テイラー展開による近似を行う際に「特定の次数までを取り扱い以降は誤差と見なす」ということはよく行われます。ここで誤差と見なす項を略記することで数式展開が行いやすくなりますが、この際に用いられるランダウの漸近記法について当記事では定義や活用例の確認を行います。
主に「大学教養 微分積分(数研出版)」の$3.4$節の「テイラーの定理」の内容を参考に作成を行いました。
・数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
ランダウの漸近記法
ランダウの漸近記法の定義
ランダウの記号$\mathcal{o}$は下記のように定義される。
$$
\large
\begin{align}
\lim_{x \to a} \frac{f(x)}{g(x)} = 0 \iff f(x) = \mathcal{o}(g(x)), \, x \to a
\end{align}
$$
上記のような記法をランダウの漸近記法という。$\mathcal{o}(g(x)), \, x \to a$は「$x$が$a$に近づくとき、$f(x)$は$g(x)$に対しはるかに小さい」を表すと解釈すれば良い。
ランダウの漸近記法の活用例
「大学教養 微分積分(数研出版)」の$3.4$節の「テイラーの定理」の例$3$の式は下記のように表せる。
$$
\large
\begin{align}
\lim_{x \to a} \frac{f(x)}{1} = \lim_{x \to a} f(x) = 0 & \iff f(x) = \mathcal{o}(1), \, x \to a \\
f(x) = 2x^2 + h(x), \, \lim_{x \to 0} \frac{h(x)}{g(x)} = 0 & \iff f(x) = 2x^2 + \mathcal{o}(x^2), \, x \to 0
\end{align}
$$
ランダウ記号の計算規則
$x \to 0$のとき下記が成立する。
$$
\large
\begin{align}
x^{m} \mathcal{o}(x^{n}) &= \mathcal{o}(x^{m+n}) \\
\mathcal{o}(x^{m}) \mathcal{o}(x^{n}) &= \mathcal{o}(x^{m+n}) \\
\mathcal{o}(x^{m}) + \mathcal{o}(x^{n}) &= \mathcal{o}(x^{l}), \, l = \min\{ m,n \}
\end{align}
$$
有限テイラー展開とランダウの漸近記法
式表記
$x \to a$における有限テイラー展開はランダウの記号を用いて下記のように表すことができる。
$$
\large
\begin{align}
f(x) = f(a) + f'(a)(x-a) + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^{n} + \mathcal{o}((x-a)^{n}), \, x \to a
\end{align}
$$
上記は「$(x-a)^{n+1}$以降の項を$\mathcal{o}((x-a)^{n})$でまとめた」と解釈すると良い。$x \to a$では$x-a$が$0$に近い値を取るので、次数が大きくなればなるほど$(x-a)^{n}$は$0$に近づくことに基づいて理解すると良い。下記を実行することで図を元に理解することができる。
import numpy as np
import matplotlib.pyplot as plt
n = np.arange(1, 11, 1)
a = 1.
x = np.array([0.9, 0.95, 0.99, 0.995, 0.999])
for i in range(x.shape[0]):
delta = (x[i]-a)**n
plt.plot(n, delta, label="x: {}".format(x[i]))
plt.legend(loc="lower right")
plt.show()・実行結果
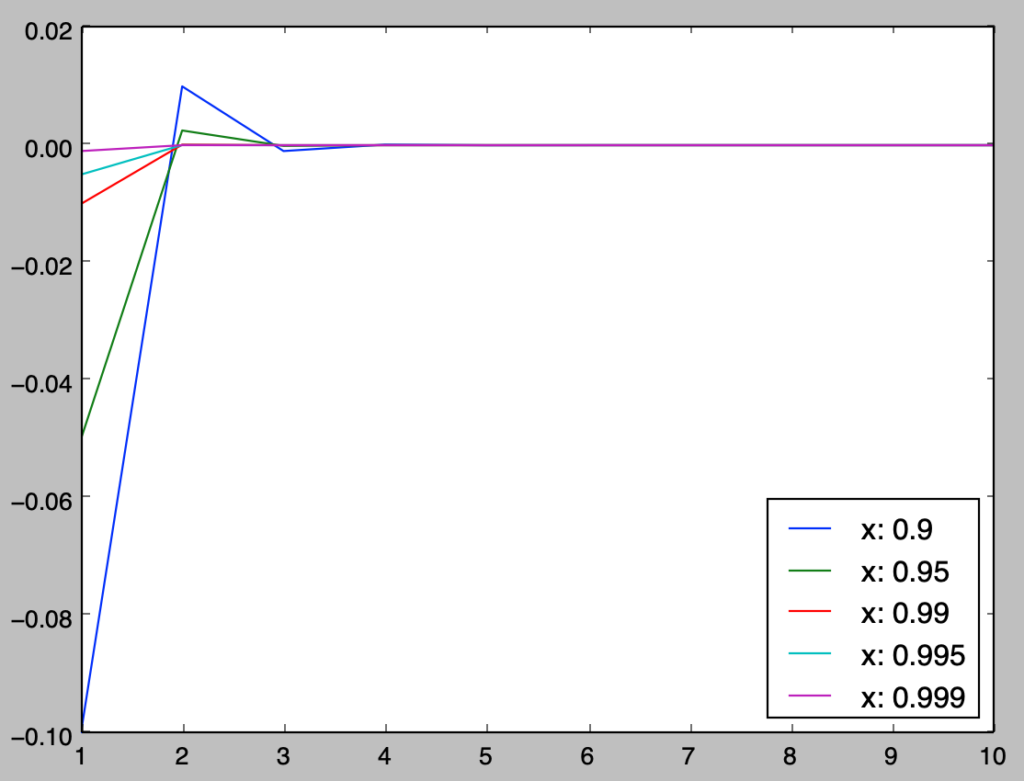
上図より、「次数が大きくなればなるほど$(x-a)^{n}$が$0$に近づくこと」が確認できる。
テイラー展開におけるランダウの漸近記法の活用例
$x=0$における$(1+x^2)e^{x}$の$5$次の漸近展開を以下行う。$e^{x}$のテイラー展開はランダウの記号を用いて下記のように表せる。
$$
\large
\begin{align}
e^{x} &= 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \frac{1}{4!} x^4 + \frac{1}{5!} x^5 + \mathcal{o}(x^5) \quad (1) \\
&= 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \mathcal{o}(x^3) \quad (2)
\end{align}
$$
$(2)$式より$x^2 e^{x}$は下記のように表せる。
$$
\large
\begin{align}
x^2 e^{x} &= x^2 (1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \mathcal{o}(x^3)) \\
&= x^2 + x^3 + \frac{1}{2!} x^4 + \frac{1}{3!} x^5 + x^2 \mathcal{o}(x^3) \\
&= x^2 + x^3 + \frac{1}{2!} x^4 + \frac{1}{3!} x^5 + \mathcal{o}(x^5) \quad (3)
\end{align}
$$
$(1), (3)$式より$(1+x^2)e^{x}$の$5$次の漸近展開は下記のように表せる。
$$
\large
\begin{align}
(1+x^2) e^{x} &= 1 + x + \left( \frac{1}{2!} + 1 \right) x^2 + \left( \frac{1}{3!} + 1 \right) x^3 + \left( \frac{1}{4!} + \frac{1}{2!} \right) x^4 + \left( \frac{1}{5!} + \frac{1}{3!} \right) x^5 + \mathcal{o}(x^5) \\
&= 1 + x + \frac{1}{2!} x^2 + \frac{7}{3!} x^3 + \frac{13}{4!} x^4 + \frac{21}{5!} x^5 + \mathcal{o}(x^5)
\end{align}
$$
上記は「大学教養 微分積分(数研出版)」の$3.4$節の「テイラーの定理」の例題$2$を元に作成を行なった。
