ブログ

解答

[1] 解答

$\boxed{ \ \mathsf{記述1}\ }$ ： $50$％

事象$X$が感染、事象$A_1$が検査$1$に陽性を表すとそれぞれ定義する。また、事象$X$の余事象を$X^{c}$のように表すと考える。

このとき、事後確率$P(X|A_1)$はベイズの定理を用いて下記のように計算できる。
$$
\large
\begin{align}
P(X|A_1) &= \frac{P(A_1|X)P(X)}{P(A_1)} \\
&= \frac{P(A_1|X)P(X)}{P(A_1)P(X) + P(A_1)P(X^c)} \\
&= \frac{0.999 \times 0.001}{0.999 \times 0.001 + 0.001 \times 0.999} = 0.5
\end{align}
$$

上記が検査$1$に陽性だった場合の本当に確率している確率を表す。

[2] 解答

$\boxed{ \ \mathsf{記述2}\ }$ ： $95$％

[1]で行なった定義に加えて、事象$A_2$は検査$2$に陽性を表すと定義する。

このとき、事後確率$P(X|A_1, A_2)$はベイズの定理を用いて下記のように計算できる。
$$
\large
\begin{align}
P(X|A_1, A_2) &= \frac{P(A_2|X,A_1)P(X,A_1)}{P(A_1, A_2)} \\
&= \frac{P(A_2|X,A_1)P(X,A_1)}{P(A_2|X,A_1)P(X,A_1) + P(A_2|X^{c},A_1)P(X^{c},A_1)} \\
&= \frac{0.95 \times 0.5}{0.95 \times 0.5 + 0.05 \times 0.5} = 0.95
\end{align}
$$

上記が検査$1$、検査$2$に陽性だった場合の本当に確率している確率を表す。

解説

分母の計算に用いた$P(A_1)=P(A_1)P(X) + P(A_1)P(X^{c})$や$P(A_1, A_2)=P(A_2|X,A_1)P(X,A_1) + P(A_2|X^{c},A_1)P(X^{c},A_1)$で表される全確率の公式はよく用いられるので抑えておくと良いと思います。

参考

・準1級関連まとめ
https://www.hello-statisticians.com/toukeikentei-semi1

Ch.8 「質的データの統計的分析」の章末問題の解答例　〜自然科学の統計学(東京大学出版会)〜

投稿日: 2022-02-252022-08-07 投稿者: lib-arts

当記事は「基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)」の読解サポートにあたってChapter.$8$の「質的データの統計的分析」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

自然科学の統計学 (基礎統計学)

下記などの演習も並行で抑えておくと良いと思います。
https://www.hello-statisticians.com/practice/stat_practice7.html

Contents

1 章末の演習問題について
2 まとめ

章末の演習問題について

問題8.1の解答例

i)
下記を実行することで$\alpha_0, \alpha_1$の推定値の$\hat{\alpha}_0, \hat{\alpha}_1$を得ることができる。

import numpy as np
from scipy import linalg

X = np.ones([5,2])
X[:,1] = np.arange(0.,5.,1)
y = np.array([0.067, 0.267, 0.500, 0.767, 0.900]).reshape([5,1])
X_ = linalg.inv(np.dot(X.T,X))
alpha = np.dot(X_,np.dot(X.T,y))

print(alpha)

・実行結果

> print(alpha)
[[ 0.067 ]
 [ 0.2166]]

上記より、$\hat{\alpha}_0=0.067, \hat{\alpha}_1=0.2166$が得られる。

ⅱ)
下記を実行することで結果を得ることができる。

import numpy as np
from scipy import linalg

X = np.ones([5,2])
X[:,1] = np.arange(0.,5.,1)
y = np.array([0.067, 0.267, 0.500, 0.767, 0.900]).reshape([5,1])
X_ = linalg.inv(np.dot(X.T,X))
alpha = np.dot(X_,np.dot(X.T,y))

print(np.dot(X,alpha))

・実行結果

> print(np.dot(X,alpha))
[[ 0.067 ]
 [ 0.2836]
 [ 0.5002]
 [ 0.7168]
 [ 0.9334]]

ⅲ)
省略

iv)
$0.2166X+0.067>1, 0.2166X+0.067<0$をそれぞれ解けばよい。
・$0.2166X+0.067>1$
$X>4.3074…$

・$0.2166X+0.067<0$
$X<-0.3093…$

問題8.2の解答例

i)
$\displaystyle P = F(\beta_{0}+\beta_{1}X) = \frac{1}{2}$は$\beta_{0}+\beta_{1}X=0$の時に成立する。よってこのときの$X$の値は下記のように導出できる。
$$
\large
\begin{align}
\beta_{0} + \beta_{1}X &= 0 \\
\beta_{1}X &= -\beta_{0} \\
X &= – \frac{\beta_{0}}{\beta_{1}}
\end{align}
$$

ⅱ)
それぞれ下記のように考えることができる。
・プロビット
$$
\large
\begin{align}
P &= F(\beta_{0}+\beta_{1}X) \\
F(Z) &= \int_{-\infty}^{Z} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx
\end{align}
$$

上記を元に$\displaystyle \frac{dP}{dX}$を計算する。
$$
\large
\begin{align}
\frac{dP}{dX} &= \frac{dP}{dZ} \cdot \frac{dZ}{dX} \\
&= \frac{1}{\sqrt{2 \pi}} e^{-\frac{Z^2}{2}} \cdot \beta_{1}
\end{align}
$$

上記を$Z$の関数と見ると、$Z=0$のとき最大値を取ることがわかる。よって、$\displaystyle \left| \frac{dP}{dX} \right|$は$\displaystyle Z=0, X = – \frac{\beta_{0}}{\beta_{1}}$のとき下記のような最大値を取る。
$$
\large
\begin{align}
\frac{1}{\sqrt{2 \pi}} e^{-\frac{0^2}{2}} \cdot \beta_{1} &= \frac{1}{\sqrt{2 \pi}} \cdot \beta_{1} \\
&= 0.3989 \beta_{1}
\end{align}
$$

・ロジット
$$
\large
\begin{align}
P &= F(\beta_{0}+\beta_{1}X) \\
F(Z) &= \frac{e^{Z}}{1+e^{Z}} \\
&= \frac{1}{1+e^{-Z}}
\end{align}
$$

$Z=\beta_{0}+\beta_{1}X$とおき、上記を元に$\displaystyle \frac{dP}{dX}$を計算する。
$$
\large
\begin{align}
\frac{dP}{dX} &= \frac{dP}{dZ} \cdot \frac{dZ}{dX} \\
&= -\frac{1}{(1+e^{-Z})^2} \cdot -e^{-Z} \cdot \beta_{1} \\
&= \frac{e^{-Z}}{(1+e^{-Z})^2} \cdot \beta_{1}
\end{align}
$$

ここで上記を最大にする$Z$がわかれば$Z=\beta_{0}+\beta_{1}X$より対応する$X$の値も計算できる。よって、以下では$\displaystyle g(Z) = \frac{e^{-Z}}{(1+e^{-Z})^2}$を最大にする$Z$を考える。
$$
\large
\begin{align}
\frac{dg(Z)}{dZ} &= \frac{d}{dZ} ((1+e^{-Z})^{-2}e^{-Z}) \\
&= -2(1+e^{-Z})^{-3} \times -e^{-Z} \times e^{-Z} + (1+e^{-Z})^{-2} \times -e^{-Z} \\
&= \frac{e^{-Z}(e^{-Z}-1)}{2(1+e^{-Z})^{3}}
\end{align}
$$

上記は単調減少かつ$Z=0$で$\displaystyle \frac{dg(Z)}{dZ}=0$なので$Z=0$のとき$g(Z)$は最大値を取る。このことは$\displaystyle \left| \frac{dP}{dX} \right|$は$\displaystyle Z=0, X = – \frac{\beta_{0}}{\beta_{1}}$のとき下記のような最大値を取ることを意味する。
$$
\large
\begin{align}
\frac{e^{-0}}{(1+e^{-0})^2} \cdot \beta_{1} &= \frac{1}{(1+1)^2} \cdot \beta_{1} \\
&= 0.25 \beta_{1}
\end{align}
$$

問題8.3の解答例

例8.2と例8.5に関してそれぞれ確認を行う。
・例8.2

print(2.324/1.086)
print(1.162/0.543)

・実行結果

> print(2.324/1.086)
2.13996316759
> print(1.162/0.543)
2.13996316759

・例8.5

print(50.26/27.56)
print(2.526/1.358)
print(0.612/0.337)

・実行結果

> print(50.26/27.56)
1.8236574746
> print(2.526/1.358)
1.86008836524
> print(0.612/0.337)
1.81602373887

$\displaystyle \frac{\pi}{\sqrt{3}} \simeq 1.81$より、例8.5で概ね成立していることが確認できる。

問題8.4の解答例

下記を実行することで結果を得ることができる。

import numpy as np

X = np.array([[0.,89.,0.], [0.,85.,0.], [1.,84.,1.], [0.,83.,0.], [1.,81.,1.], [0.,88.,1.], [1.,87.,0.], [1.,86.,0.], [0.,86.,1.], [1.,84.,10.], [0.,87.,0.], [1.,83.,1.], [1.,82.,1.], [0.,83.,0.], [0.,82.,0.], [0.,86.,0.], [0.,78.,0.], [0.,77.,1.], [0.,85.,1.], [1.,75.,1.], [1.,80.,0.], [1.,82.,0.], [1.,79.,1.], [0.,83.,1.], [0.,82.,1.], [0.,89.,0.], [1.,86.,1.], [1.,80.,1.], [1.,81.,0.], [0.,78.,0.]])
y = np.array([1., 1., 0., 1., 0., 1., 0., 0., 1., 0., 1., 0., 0., 1., 0., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0., 1., 1., 0., 1., 0.])

y_probit = -27.56 - 1.358*X[:,0] + 0.337*X[:,1] - 0.447*X[:,2]
y_probit[y_probit>0] = 1
y_probit[y_probit<=0] = 0
y_logi = -50.26 - 2.526*X[:,0] + 0.612*X[:,1] - 0.610*X[:,2]
y_logi[y_logi>0] = 1
y_logi[y_logi<=0] = 0

print(np.float(np.sum(y==y_probit))/y.shape[0])
print(np.float(np.sum(y==y_logi))/y.shape[0])

・実行結果

> print(np.float(np.sum(y==y_probit))/y.shape[0])
0.833333333333
> print(np.float(np.sum(y==y_logi))/y.shape[0])
0.9

上記より正答率はプロビットに対して$83.3$％、ロジットに対して$90.0$％であることがわかる。

問題8.5の解答例

まとめ

自然科学の統計学 (基礎統計学)

Ch.2 「線形モデルと最小二乗法」の章末問題の解答例　〜自然科学の統計学(東京大学出版会)〜

投稿日: 2022-02-232022-08-07 投稿者: lib-arts

当記事は「基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)」の読解サポートにあたってChapter.$2$の「線形モデルと最小二乗法」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

自然科学の統計学 (基礎統計学)

Contents

1 章末の演習問題について

章末の演習問題について

問題2.1の解答例

i)
$[0,1]$の一様乱数に関してはNumPyのrandom.randを用いて$y_i$の生成を行う。

import numpy as np

np.random.seed(0)
u = np.random.rand(10,12)
epsilon = np.sum(u,axis=1)-6.
y = 15. + epsilon

print(y)

・実行結果

> print(y)
[ 16.47828279  16.17259914  14.48252679  15.08570806  13.76567862
  13.92641329  13.66679521  14.26112406  15.07466738  16.7132275 ]

ⅱ)
下記を実行することで$y_{ij}, i=1,2,…,5, j=1,2,…,5$の生成を行う。

import numpy as np

np.random.seed(0)
u = np.random.rand(5,5,12)
epsilon = np.sum(u,axis=2)-6.
y = np.array([np.repeat(2.,5), np.repeat(4.,5), np.repeat(6.,5), np.repeat(8.,5), np.repeat(10.,5)]) + epsilon

print(y)

・実行結果

> print(y)
[[  3.47828279   3.17259914   1.48252679   2.08570806   0.76567862]
 [  2.92641329   2.66679521   3.26112406   4.07466738   5.7132275 ]
 [  6.17470405   6.49753858   7.01033545   6.79519637   4.72282185]
 [  7.92514854   6.90028678   7.57093465   8.73749154   7.02365745]
 [  9.42140393  10.17896516  11.20754253  10.97396766  10.28374057]]

ⅲ)
下記を実行することで$y_i$の生成を行う。

import numpy as np

np.random.seed(0)
u = np.random.rand(10,12)
x = np.arange(1.,11.,1)
epsilon = np.sum(u,axis=1)-6.
y = 10-5*x+2*x**2+epsilon

print(y)

・実行結果

> print(y)
[   8.47828279    9.17259914   12.48252679   22.08570806   33.76567862
   50.92641329   71.66679521   97.26112406  127.07466738  161.7132275 ]

問題2.2の解答例

数式よりもNumPy形式の方が取り扱いやすいので、以下NumPy形式で表す。
i)
下記を実行することで$\mathbf{X}, \mathbf{X}^{T}\mathbf{X}, \mathbf{X}^{T}\mathbf{y}$を表すことができる。

import numpy as np

X = np.ones([10,1])
y = np.array([16.47828279, 16.17259914, 14.48252679, 15.08570806, 13.76567862, 13.92641329, 13.66679521, 14.26112406, 15.07466738, 16.7132275]).reshape([10,1])

print(X)
print(np.dot(X.T,X))
print(np.dot(X.T,y))

・実行結果

> print(X)
[[ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]]
> print(np.dot(X.T,X))
[[ 10.]]
> print(np.dot(X.T,y))
[[ 149.62702284]]

ⅱ)
下記を実行することで$\mathbf{X}, \mathbf{X}^{T}\mathbf{X}, \mathbf{X}^{T}\mathbf{y}$を表すことができる。

import numpy as np

X = np.zeros([25,6])
X[:,0] = 1.
X[0:5,1] = 1.
X[5:10,2] = 1.
X[10:15,3] = 1.
X[15:20,4] = 1.
X[20:25,5] = 1.
y = np.array([[3.47828279, 3.17259914, 1.48252679, 2.08570806, 0.76567862], [  2.92641329, 2.66679521, 3.26112406, 4.07466738, 5.7132275], [6.17470405, 6.49753858, 7.01033545, 6.79519637, 4.72282185], [7.92514854, 6.90028678, 7.57093465, 8.73749154, 7.02365745], [9.42140393, 10.17896516, 11.20754253, 10.97396766, 10.28374057]]).reshape([25,1])

print(X)
print(np.dot(X.T,X))
print(np.dot(X.T,y))

・実行結果

> print(X)
[[ 1.  1.  0.  0.  0.  0.]
 [ 1.  1.  0.  0.  0.  0.]
 [ 1.  1.  0.  0.  0.  0.]
...
 [ 1.  0.  0.  0.  0.  1.]
 [ 1.  0.  0.  0.  0.  1.]
 [ 1.  0.  0.  0.  0.  1.]
 [ 1.  0.  0.  0.  0.  1.]]
> print(np.dot(X.T,X))
[[ 25.   5.   5.   5.   5.   5.]
 [  5.   5.   0.   0.   0.   0.]
 [  5.   0.   5.   0.   0.   0.]
 [  5.   0.   0.   5.   0.   0.]
 [  5.   0.   0.   0.   5.   0.]
 [  5.   0.   0.   0.   0.   5.]]
> print(np.dot(X.T,y))
[[ 151.05075795]
 [  10.9847954 ]
 [  18.64222744]
 [  31.2005963 ]
 [  38.15751896]
 [  52.06561985]]

ⅲ)
下記を実行することで$\mathbf{X}, \mathbf{X}^{T}\mathbf{X}, \mathbf{X}^{T}\mathbf{y}$を表すことができる。

import numpy as np

X = np.ones([10,3])
X[:,1] = np.arange(1.,11.,1)
X[:,2] = X[:,1]**2
y = np.array([8.47828279, 9.17259914, 12.48252679, 22.08570806, 33.76567862, 50.92641329, 71.66679521, 97.26112406, 127.07466738, 161.7132275]).reshape([10,1])

print(X)
print(np.dot(X.T,X))
print(np.dot(X.T,y))

・実行結果

> print(X)
[[   1.    1.    1.]
 [   1.    2.    4.]
 [   1.    3.    9.]
 [   1.    4.   16.]
 [   1.    5.   25.]
 [   1.    6.   36.]
 [   1.    7.   49.]
 [   1.    8.   64.]
 [   1.    9.   81.]
 [   1.   10.  100.]]
> print(np.dot(X.T,X))
[[  1.00000000e+01   5.50000000e+01   3.85000000e+02]
 [  5.50000000e+01   3.85000000e+02   3.02500000e+03]
 [  3.85000000e+02   3.02500000e+03   2.53330000e+04]]
> print(np.dot(X.T,y))
[[   594.62702284]
 [  4667.56160689]
 [ 39389.13130627]]

問題2.3の解答例

scipy.linalg.invを用いて逆行列の計算を行う。
i)

import numpy as np
from scipy import linalg

X = np.ones([10,1])
y = np.array([16.47828279, 16.17259914, 14.48252679, 15.08570806, 13.76567862, 13.92641329, 13.66679521, 14.26112406, 15.07466738, 16.7132275]).reshape([10,1])
X_ = linalg.inv(np.dot(X.T,X))
theta = np.dot(X_,np.dot(X.T,y))

print(theta)

・実行結果

> print(theta)
[[ 14.96270228]]

ⅱ)
省略

ⅲ)

import numpy as np
from scipy import linalg

X = np.ones([10,3])
X[:,1] = np.arange(1.,11.,1)
X[:,2] = X[:,1]**2
y = np.array([8.47828279, 9.17259914, 12.48252679, 22.08570806, 33.76567862, 50.92641329, 71.66679521, 97.26112406, 127.07466738, 161.7132275]).reshape([10,1])
X_ = linalg.inv(np.dot(X.T,X))
theta = np.dot(X_,np.dot(X.T,y))

print(theta)

・実行結果

> print(theta)
[[ 13.31134241]
 [ -6.56004997]
 [  2.13588662]]

問題2.4の解答例

・備考
少々問題文の意図がわかりにくい印象だったので、ⅱ)の答えを先に確認した後に取り組む方が良いと思います。

i)
下記を実行することでそれぞれ計算を行うことができる。

import numpy as np

x, y = np.zeros([11,4]), np.zeros([11,4])
x[:,0], x[:,1], x[:,2] = np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.]), np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.]), np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.])
x[:,3] = np.array([8., 8., 8., 8., 8., 8., 8., 19., 8., 8., 8.])
y[:,0] = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])
y[:,1] = np.array([9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74])
y[:,2] = np.array([7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73])
y[:,3] = np.array([6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])

s_x, s_y, s_xy = np.sum((x-np.mean(x))**2, axis=0)/(x.shape[0]-1), np.sum((y-np.mean(y))**2, axis=0)/(x.shape[0]-1), np.sum((x-np.mean(x))*(y-np.mean(y)), axis=0)/(x.shape[0]-1)
r = s_xy/np.sqrt(s_x*s_y)

beta = np.zeros([4,2])
beta[:,1] = s_xy/s_x
beta[:,0] = np.mean(y)-beta[:,1]*np.mean(x,axis=0)

S_xx = np.sum((x-np.mean(x))**2, axis=0)
S_xy = np.sum((x-np.mean(x))*(y-np.mean(y)), axis=0)

e = y[:,0]-(beta[0,0]+beta[0,1]*x[:,0])
s_beta = np.sqrt(np.sum(e**2)/((x.shape[0]-2)*np.sum((x[:,0]-np.mean(x,axis=0)[0])**2)))
t = (beta[0,1]-0.)/s_beta

print("a. n: {}".format(x.shape[0]))
print("b. mean_x: {:.1f}".format(np.mean(x,axis=0)[0]))
print("c. mean_y: {:.1f}".format(np.mean(y,axis=0)[0]))
print("d. mean_y: {:.3f}".format(r[0]))
print("e. estimated beta_1: {:.1f}".format(beta[0,1]))
print("f. linear func: y = {:.0f} + {:.1f}x".format(beta[0,0],beta[0,1]))
print("g. S_xx: {:.1f}".format(S_xx[0]))
print("h. S_xy: {:.2f}".format(S_xy[0]))
print("i. {:.2f}".format(S_xy**2/S_xx))
print("j. t: {:.2f}".format(t))

・実行結果

a. n: 11
b. mean_x: 9.0
c. mean_y: 7.5
d. mean_y: 0.816
e. estimated beta_1: 0.5
f. linear func: y = 3 + 0.5x
g. S_xx: 110.0
h. S_xy: 54.99
i. 27.49
j. t: 4.24

なお、結果は巻末の解答に合わせて$(x_1,y_1)$に関するもののみを出力したが、それぞれの変数には他の値も格納した。どの$(x_i,y_i)$の組に対しても$(x_1,y_1)$と同様の結果が得られることは抑えておくと良い。

ⅱ)

import numpy as np
import matplotlib.pyplot as plt

x, y = np.zeros([11,4]), np.zeros([11,4])
x[:,0], x[:,1], x[:,2] = np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.]), np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.]), np.array([10., 8., 13., 9., 11., 14., 6., 4., 12., 7., 5.])
x[:,3] = np.array([8., 8., 8., 8., 8., 8., 8., 19., 8., 8., 8.])
y[:,0] = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])
y[:,1] = np.array([9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74])
y[:,2] = np.array([7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73])
y[:,3] = np.array([6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])

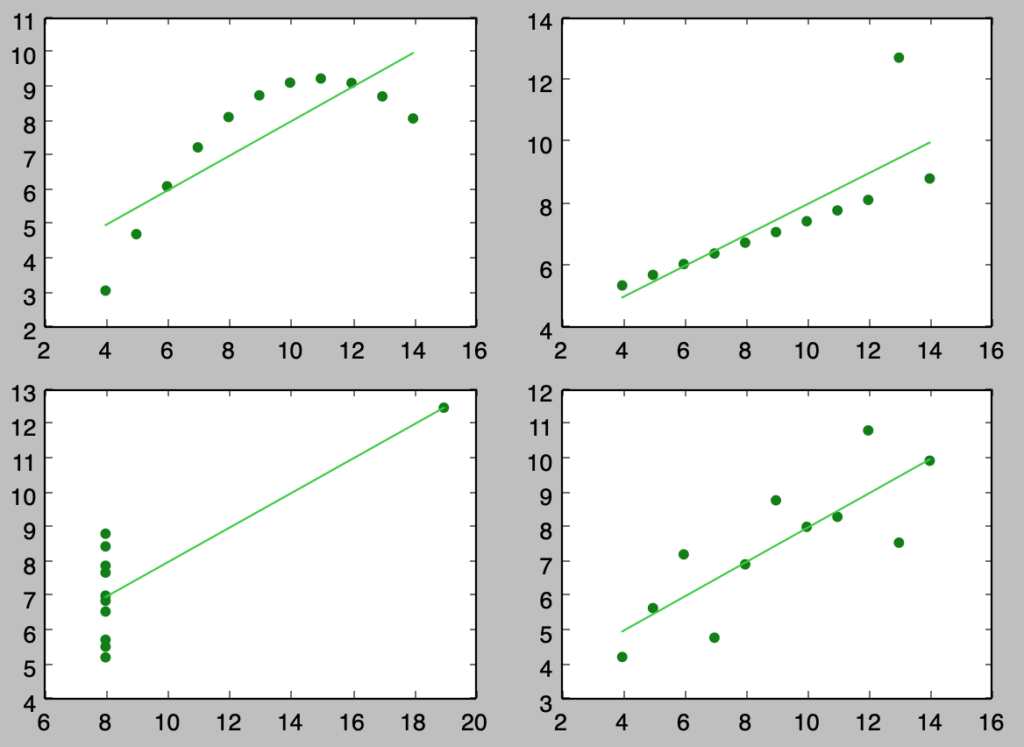
for i in range(x.shape[1]):
    plt.subplot(2,2,i)
    plt.scatter(x[:,i],y[:,i],color="green")
    plt.plot(x[:,i],beta[0]+beta[1]*x[:,i],color="limegreen")

plt.show()

・実行結果

上記のように散布図を描くことで、全く異なる分布であるにも関わらず同じ係数が推定される場合があることに注意が必要であることがわかる。

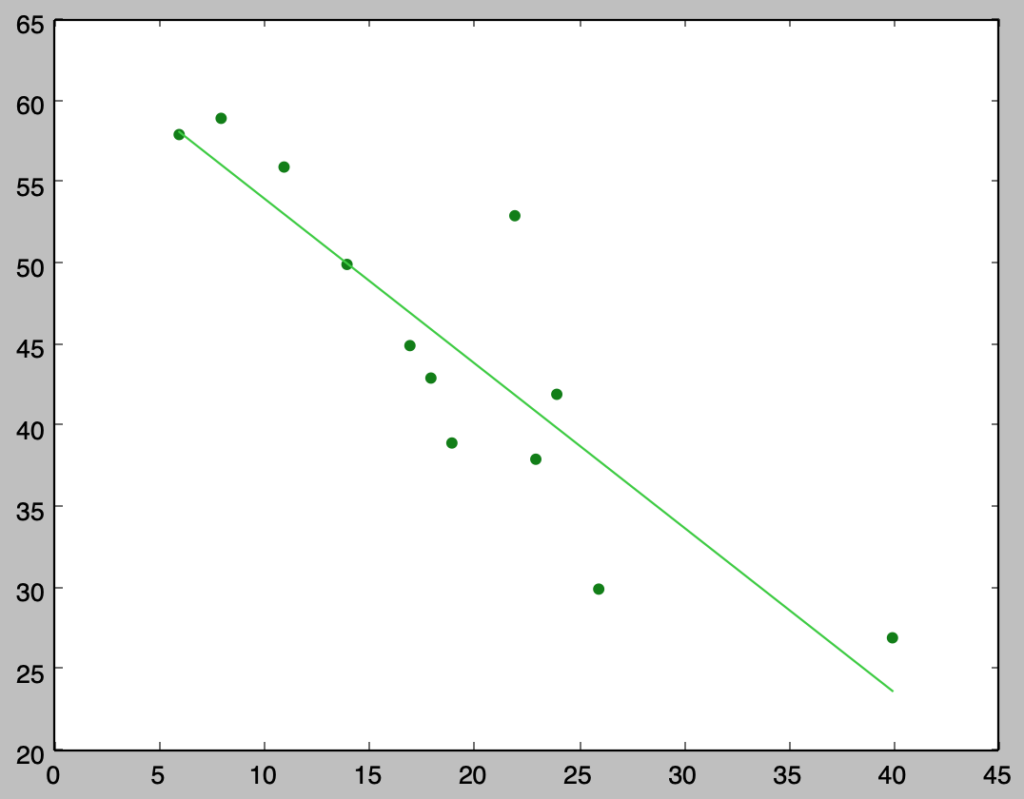
問題2.5の解答例

問題2.6の解答例

下記を実行することで回帰係数の推定と、散布図や回帰式の図示を行うことができる。

import numpy as np
import matplotlib.pyplot as plt

x = np.array([8., 6., 11., 22., 14., 17., 18., 24., 19., 23., 26., 40.])
y = np.array([59., 58., 56., 53., 50., 45., 43., 42., 39., 38., 30., 27.])

beta = np.zeros(2)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y)-beta[1]*np.mean(x)

print("beta_0: {:.3f}".format(beta[0]))
print("beta_1: {:.3f}".format(beta[1]))

plt.scatter(x,y,color="green")
plt.plot(x,beta[0]+beta[1]*x,color="limegreen")
plt.show()

・実行結果

> plt.scatter(x,y,color="green")
beta_0: 64.247
> print("beta_1: {:.3f}".format(beta[1]))
beta_1: -1.013

また、下記を実行することで帰無仮説$H_0: \beta_1=0$に関する検定を行うことができる。

import numpy as np
from scipy import stats

x = np.array([8., 6., 11., 22., 14., 17., 18., 24., 19., 23., 26., 40.])
y = np.array([59., 58., 56., 53., 50., 45., 43., 42., 39., 38., 30., 27.])

beta = np.zeros(2)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y)-beta[1]*np.mean(x)

e = y-(beta[0]+beta[1]*x)
s_e = np.sqrt(np.sum(e**2)/(x.shape[0]-2))
s_beta = s_e/np.sqrt(np.sum((x-np.mean(x))**2))

t = (beta[1]-0)/s_beta

if np.abs(t) > stats.t.ppf(1.-0.025,x.shape[0]-2):
    print("t: {:.2f}, reject H_0.".format(t))
else:
    print("t: {:.2f}, accept H_0.".format(t))

・実行結果

t: -5.88, reject H_0.

問題2.7の解答例

i)
P.45の議論を元に導出を行う。
$x$の平均を$\bar{x}$、$y$の平均を$\bar{y}$、$\displaystyle S_{xx}=\sum_{i=1}^{15} (x_i-\bar{x})^2$、$\displaystyle S_{xy}=\sum_{i=1}^{15} (x_i-\bar{x})(y_i-\bar{y})$とする。このとき、それぞれの値は下記のように計算できる。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{15}(7.2+4.8+5.2+4.9+5.4+6.4+6.8+8.0 \\
&+6.0+6.7+7.0+8.0+7.3+4.6+4.2) \\
&= 6.1666… \\
\bar{y} &= \frac{1}{15}(8.4+5.4+6.3+6.8+8.0+11.1+12.3+13.3 \\
&+8.4+9.5+10.4+12.7+10.3+7.0+5.1) \\
&= 9.0 \\
S_{xx} &= (7.2-6.167)^2+… \\
&= 21.853 \\
S_{xy} &=(7.2-6.167)(8.4-9.0)+… \\
&= 41.520
\end{align}
$$
このとき下記が成立する。
$$
\large
\begin{align}
y &= \bar{y}+\frac{S_{xy}}{S_{xx}}(x-\bar{x}) \\
&= 9+\frac{21.853}{41.520}(x-6.167) \\
&= 1.9x-2.716
\end{align}
$$
上記より、$\beta_{0}=-2.716$、$\beta_{1}=1.9$が成立する。

ⅱ)
i)で求めた$y=1.9x-2.716$に$x=6.9$を代入する。
$$
\large
\begin{align}
y &= 1.9x-2.716 \\
&= 1.9 \times 6.9 – 2.716 \\
&= 10.39
\end{align}
$$

ⅲ)
下記を実行することで計算を行うことができる。

import numpy as np
from scipy import stats

x = np.array([7.2, 4.8, 5.2, 4.9, 5.4, 6.4, 6.8, 8.0, 6.0, 6.7, 7.0, 8.0, 7.3, 4.6, 4.2])
y = np.array([8.4, 5.4, 6.3, 6.8, 8.0, 11.1, 12.3, 13.3, 8.4, 9.5, 10.4, 12.7, 10.3, 7.0, 5.1])

s_x = np.sum((x-np.mean(x))**2)
s_xy = np.sum((x-np.mean(x))*(y-np.mean(y)))

beta = np.zeros(2)
beta[1] = s_xy/s_x
beta[0] = np.mean(y)-beta[1]*np.mean(x)

expected_y = beta[0] + beta[1]*6.9

sigma2 = (np.sum(y**2)-np.sum(y)**2/x.shape[0]-s_xy**2/s_x)/(x.shape[0]-2)
y_range = np.sqrt((1./x.shape[0]+(6.9-np.mean(x))/s_x)*sigma2)

interval_y = np.array([expected_y+stats.t.ppf(0.025,x.shape[0]-2)*y_range, expected_y+stats.t.ppf(0.975,x.shape[0]-2)*y_range])

print(interval_y)

・実行結果

> print(interval_y)
array([  9.57708628,  11.2094909 ])

iv)
下記を実行することで$H_0: \beta_1=2$の検定を行うことができる。

import numpy as np
from scipy import stats

x = np.array([7.2, 4.8, 5.2, 4.9, 5.4, 6.4, 6.8, 8.0, 6.0, 6.7, 7.0, 8.0, 7.3, 4.6, 4.2])
y = np.array([8.4, 5.4, 6.3, 6.8, 8.0, 11.1, 12.3, 13.3, 8.4, 9.5, 10.4, 12.7, 10.3, 7.0, 5.1])

beta = np.zeros(2)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y)-beta[1]*np.mean(x)

expected_y = beta[0] + beta[1]*6.9

e = y - (beta[0]+beta[1]*x)
s_error = np.sqrt(np.sum(e**2)/(x.shape[0]-2))
s_error_beta = s_error/np.sqrt(np.sum((x-np.mean(x))**2))

t = (beta[1]-2.)/s_error_beta
if np.abs(t)>stats.t.ppf(1.-0.025,x.shape[0]-2):
    print("t: {:.3f}, reject H_0".format(t))
else:
    print("t: {:.3f}, accept H_0".format(t))

・実行結果

t: -0.392, accept H_0

問題2.8の解答例

問題2.9の解答例

問題2.10の解答例

i)
誤差項$\epsilon_i$に関して、二乗和を考えると下記のように表すことができる。
$$
\large
\begin{align}
\sum_{i=1}^{n} \epsilon_i^2 = \sum_{i=1}^{n} (y_i – \beta x_i)^2
\end{align}
$$

上記を$\beta$で偏微分し、正規方程式を考え、下記のように$\beta$に関して解く。
$$
\large
\begin{align}
\frac{\partial}{\partial \beta} \sum_{i=1}^{n} (y_i – \beta x_i)^2 &= 0 \\
-2 \sum_{i=1}^{n} (y_i – \beta x_i) x_i &= 0 \\
\sum_{i=1}^{n} x_i y_i &= \beta \sum_{i=1}^{n} x_i^2 \\
\beta \sum_{i=1}^{n} x_i^2 &= \sum_{i=1}^{n} x_i y_i \\
\beta &= \frac{\sum_{i=1}^{n} x_i y_i}{\sum_{i=1}^{n} x_i^2}
\end{align}
$$

よって$\beta$の最小二乗推定量$\hat{\beta}$は下記のように表すことができる。
$$
\large
\begin{align}
\hat{\beta} = \frac{\sum_{i=1}^{n} x_i y_i}{\sum_{i=1}^{n} x_i^2}
\end{align}
$$

自然科学の統計学 (基礎統計学)

「統計学実践ワークブック」演習問題etc Ch.20 「分散分析と実験計画法」

投稿日: 2022-02-212022-08-07 投稿者: lib-arts

当記事は「統計学実践ワークブック(学術図書出版社)」の読解サポートにあたってChapter.20の「分散分析と実験計画法」に関して演習問題を中心に解説を行います。「分散分析と実験計画法」は少々手順が複雑なので、演習を通して抑えておくと良いと思われました。

日本統計学会公式認定統計検定準1級対応統計学実践ワークブック

3,080円(11/10 13:44時点)

Contents

1 本章のまとめ
2 演習問題解説
3 参考文献

本章のまとめ

分散分析に関しては下記などで取りまとめを行なった。
https://www.hello-statisticians.com/explain-terms-cat/k_sample_problem1.html

演習問題解説

問20.1

$[1]$
×
ランダム化の原則に基づいて、苗の大小に関係なく、ランダムに肥料$A_1, A_2$を割り当てる必要がある。

$[2]$
×
局所管理の原則に基づいて、均一と見なし得る$8$つの区画それぞれで肥料$A_1, A_2$の違いを実験する必要がある。

$[3]$
×
反復・繰り返しの原則と、局所管理の原則に基づいて、$A_1, A_2$のそれぞれで複数回の収穫値を観測できるように区画をいくつかに分けた上で実験を行うと良い。

問20.2

$[1]$
予測式は下記のようになる。
$$
\large
\begin{align}
y_{ij} = \mu + \alpha_{i} + \epsilon_{ij} \quad i=1, 2, …, 4; j=1, 2, …, n_i
\end{align}
$$

帰無仮説$H_{0}$は「研磨機械に差がない」ことを表す$\alpha_{1}=\alpha_{2}=…=\alpha_{4}=0$、対立仮説は「研磨機械の少なくとも$1$つに差がある」ことを表す。

$[2]$
因子$A$の水準間平方和$S_A$、誤差平方和$S_E$はそれぞれ下記のように表される。
$$
\large
\begin{align}
S_A &= \sum_{i=1}^{4} \sum_{j=1}^{n_{i}} (\bar{y}_{A_{i}}-\bar{y})^2 \\
S_E &= \sum_{i=1}^{4} \sum_{j=1}^{n_{i}} (y_{ij}-\bar{y}_{A_{i}})^2
\end{align}
$$

上記は下記を実行することでそれぞれの値を得ることができる。

import numpy as np

y_1 = np.array([15., 13., 15., 16., 14.])
y_2 = np.array([18., 17., 16., 15., 18.])
y_3 = np.array([19., 16., 17., 18.])
y_4 = np.array([17., 15., 16.])
y = [y_1, y_2, y_3, y_4]
y_average_A = [np.sum(y_1)/y_1.shape[0], np.sum(y_2)/y_2.shape[0], np.sum(y_3)/y_3.shape[0], np.sum(y_4)/y_4.shape[0]]
y_average = (np.sum(y_1)+np.sum(y_2)+np.sum(y_3)+np.sum(y_4))/17.

S_A = 0
S_E = 0
for i in range(4):
    S_A += np.sum(y[i].shape[0]*(y_average_A[i]-y_average)**2)
    S_E += np.sum((y[i]-y_average_A[i])**2)

print(S_A, S_E)
print(S_A/3., S_E/13.)
print((S_A/3.)/(S_E/13.))

・実行結果

> print(S_A, S_E)
(21.47058823529413, 19.0)
> print(S_A/3., S_E/13.)
(7.1568627450980431, 1.4615384615384615)
> print((S_A/3.)/(S_E/13.))
4.89680082559

上記の実行結果に基づいて下記の表を得ることができる。
$$
\large
\begin{array}{|c|*4{c|}}\hline \mathrm{machine} & S & \phi & V & F \\
\hline A & 21.47 & 3 & 7.157 & 4.897 \\
\hline \mathrm{error} & 19.00 & 13 & 1.462 & \\
\hline
\end{array}
$$

$F$値の$4.897$は自由度$(3,13)$の$F$分布の上側$5%$点の$F_{\alpha=0.05}(3,13)=3.41$を上回るので帰無仮説$H_0$を棄却し、対立仮説$H_1$を採択する。すなわち、「有意水準$5%$で機械により生産個数の母平均が異なる」と考えることができる。

$[3]$
点推定値$\bar{y}_{A_{3}}$とその$95$％区間$\bar{y}_{A_{3}} \pm t_{\alpha=0.025}(\phi_{E}) \sqrt{V_E/n_3}$は下記のように求めることができる。
$$
\large
\begin{align}
\bar{y}_{A_{3}} &= 17.5 \\
\bar{y}_{A_{3}} \pm t_{\alpha=0.025}(\phi_{E}) \sqrt{\frac{V_E}{n_3}} &= 17.5 \pm 2.16 \times \sqrt{\frac{1.462}{4}} \\
&= 17.5 \pm 1.31
\end{align}
$$

問20.3

$[1]$
×
Aの$1$元配置分散分析とA,Bの$2$元配置分散分析では誤差分散は異なる値を取る。

$[2]$
×
Aの平方和は$1$元配置分散分析と$2$元配置分散分析のどちらも変わらない。

$[3]$
○

問20.4

$[1]$
$S_{A \times B} = S_{T} – S_{A} – S_{B} – S_{E}$などを元に値を計算することで、下記のような分散分析表を作成することができる。
$$
\large
\begin{array}{|c|*4{c|}}\hline & S & \phi & V & F \\
\hline A & 3.00 & 3 & 3.00 & 4.50 \\
\hline B & 18.00 & 3 & 9.00 & 13.50 \\
\hline A \times B & 32.00 & 2 & 16.00 & 24.00 \\
\hline \mathrm{error} & 4.00 & 6 & 0.67 & \\
\hline \mathrm{Total} & 57.00 & 11 & & \\
\hline
\end{array}
$$

上記と$F_{\alpha=0.05}(3,6), F_{\alpha=0.05}(2,6)$などを比較することにより、$B$の主効果と$A \times B$の交互作用が有意水準$5$％で効果があると判断することができる。

$[2]$
$B$の主効果と交互作用$A \times B$が存在するので、$A, B$を組み合わせた表から$y$を大きくする$A, B$の水準を選べばよく、$A_2, B_3$の組み合わせがこれに該当する。

問20.5

$[1]$
予測式は下記のようになる。
$$
\large
\begin{align}
y_{ij} = \mu + \alpha_{i} + \beta_{j} + (\alpha \beta)_{ij} + \epsilon_{ijk}
\end{align}
$$

分散分析表は下記のように表せる。
$$
\large
\begin{array}{|c|*4{c|}}\hline & S & \phi & V & F \\
\hline A & 320.0 & 1 & 320.0 & 1.77 \\
\hline B & 125.0 & 1 & 125.0 & 0.69 \\
\hline A \times B & 320.0 & 1 & 320.0 & 1.77 \\
\hline \mathrm{error} & 2891.2 & 16 & 180.7 & \\
\hline \mathrm{Total} & 3656.2 & 19 & & \\
\hline
\end{array}
$$

上記より、$A, B$の主効果、交互作用$A \times B$は$5$％で有意とならない。

$[2]$
予測式は下記のようになる。
$$
\large
\begin{align}
y_{ij} = \mu + \alpha_{i} + \beta_{j} + (\alpha \beta)_{ij} + \gamma_{k} + \epsilon_{ijk}
\end{align}
$$

分散分析表は下記のように表せる。
$$
\large
\begin{array}{|c|*4{c|}}\hline & S & \phi & V & F \\
\hline A & 320.0 & 1 & 320.0 & 132.41 \\
\hline B & 125.0 & 1 & 125.0 & 51.72 \\
\hline A \times B & 320.0 & 1 & 320.0 & 132.41 \\
\hline V & 320.0 & 4 & 715.6 & 296.06 \\
\hline \mathrm{error} & 2862.2 & 12 & 2.42 & \\
\hline \mathrm{Total} & 3656.2 & 19 & & \\
\hline
\end{array}
$$

上記より、$A, B, V$の主効果、交互作用$A \times B$は$5$％で有意となる。

$[3]$
ブロック因子による変動が大きい場合には$[2]$のように誤差から分離する方が$A, B$などの効果の検出がしやすい。一方で、ブロック因子による変動がほとんどない場合にブロック因子を導入すると誤差の自由度が小さくなることで$A, B$などの効果の検出が行いにくくなる。

問20.6

$[1]$
直交表$L_8(2^7)$から第$[1]$列、第$[2]$列、第$[4]$列、第$[7]$列をそれぞれ$A,B,C,D$に対応すれば良いので、一部実施要因計画は下記のように表せる。
$$
\large
\begin{array}{|c|*4{c|}}\hline No. & A & B & C & D \\
\hline 1 & 1 & 1 & 1 & 1 \\
\hline 2 & 1 & 1 & 2 & 2 \\
\hline 3 & 1 & 2 & 1 & 2 \\
\hline 4 & 1 & 2 & 2 & 1 \\
\hline 5 & 2 & 1 & 1 & 2 \\
\hline 6 & 2 & 1 & 2 & 1 \\
\hline 7 & 2 & 2 & 1 & 1 \\
\hline 8 & 2 & 2 & 2 & 2 \\
\hline
\end{array}
$$

$[2]$
i) 主効果と$2$因子交互作用が交絡する組み合わせはない。
ⅱ) $2$因子交互作用は選ばなかった残りの$2$因子からなる$2$因子交互作用と交絡する。

$[3]$
$[1]$の$D$の列のみ$A \times B$に置き換えることで、一部実施要因計画は下記のように表すことができる。
$$
\large
\begin{array}{|c|*4{c|}}\hline No. & A & B & C & D \\
\hline 1 & 1 & 1 & 1 & 1 \\
\hline 2 & 1 & 1 & 2 & 1 \\
\hline 3 & 1 & 2 & 1 & 2 \\
\hline 4 & 1 & 2 & 2 & 2 \\
\hline 5 & 2 & 1 & 1 & 2 \\
\hline 6 & 2 & 1 & 2 & 2 \\
\hline 7 & 2 & 2 & 1 & 1 \\
\hline 8 & 2 & 2 & 2 & 1 \\
\hline
\end{array}
$$
上記を確認することで、$D$と$A,B,C$が直交することが確認できる。

$[4]$
i) $A$の主効果と$B \times D$、$B$の主効果と$A \times D$、$D$の主効果と$A \times B$が行楽する。
ⅱ) 行楽する$2$因子交互作用の組み合わせはない。

$[5]$
$C$の主効果や$C$に関連する$2$因子交互作用を調べる場合には$C$の主効果や$A \times C, B \times C, C \times D$の交絡がない$[3]$の計画を用いると良い。それ以外の場合では$[1]$の計画を用いると良い。

問20.7

$[1]$
交互作用$A \times B$は第$[3]$列、交互作用$A \times C$は第$[5]$列に現れる。

$[2]$
成分記号を元に$A \times B, A \times C, A \times D, B \times C, B \times D, C \times D$が対応する成分記号を考えると下記が得られる。
$$
\large
\begin{array}{|c|*2{c|}}\hline & \mathrm{abc} & \mathrm{column} \\
\hline A \times B & ab & [3] \\
\hline A \times C & ac & [5] \\
\hline A \times D & a^2bc=bc & [6] \\
\hline B \times C & bc & [6] \\
\hline B \times D & ab^2c=ac & [5] \\
\hline C \times D & abc^2=ab & [3] \\
\hline
\end{array}
$$

上記より、$A,B,C,D$の$2$因子交互作用同士は交絡する組み合わせがある一方で、主効果と$2$因子交互作用は交絡せず直交することがわかる。

$[3]$
分散分析表は下記のように作成できる。
$$
\large
\begin{array}{|c|*4{c|}}\hline & S & \phi & V & F \\
\hline A & 171.125 & 1 & 171.125 & 6.084 \\
\hline B & 45.125 & 1 & 45.125 & 1.604 \\
\hline C & 66.125 & 1 & 66.125 & 2.351 \\
\hline D & 6.125 & 1 & 6.125 & 0.218 \\
\hline A \times B & 3.125 & 1 & 0.111 \\
\hline A \times C & 136.125 & 1 & 4.840 \\
\hline \mathrm{error} & 28.125 & 1 & 28.125 & \\
\hline \mathrm{Total} & 455.875 & 7 & & \\
\hline
\end{array}
$$

$[4]$
$F$検定統計量に$F=2$を用いる場合、$[3]$で作成を行なった表より、$A, C, A \times C$を考慮する必要があることがわかる。また、応答$y$の値を小さくするにあたっては$A_1,C_2$の組み合わせが良いことが読み取れる。

参考文献

Ch.11 「乱数の性質」の章末問題の解答例　〜基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)〜

投稿日: 2022-02-212023-01-21 投稿者: lib-arts

当記事は「基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)」の読解サポートにあたってChapter.11の「乱数の性質」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

自然科学の統計学 (基礎統計学)

Contents

1 章末の演習問題について
2 まとめ

章末の演習問題について

問題11.1の解答例

Pythonの乱数生成について確認する。
https://docs.python.org/ja/3/library/random.html
上記によると周期$2^{19937}-1$のメルセンヌツイスタ(Mersenne Twister)を用いるとされている。メルセンヌツイスタは$11.2.2$節で取り扱われているM系列を元に発展させた手法で、下記が製作者の講演資料のため参考になる。

（http://www.math.sci.hiroshima-u.ac.jp/m-mat/TEACH/ichimura-sho-koen.pdf より）

実装は下記より確認できる。
http://www.math.sci.hiroshima-u.ac.jp/m-mat/MT/MT2002/CODES/mt19937ar.c

メルセンヌツイスタ法に関しては下記で詳しく取り扱った。

メルセンヌ・ツイスタ(Mersenne Twister)法まとめ

問題11.2の解答例

下記を実行することで、乗算合同法に基づき表$11.2$と同様の結果を得ることができる。

a = 16807
M = 2**31-1
X_i = 1

for i in range(15):
    X_i = X_i*a%M
    print("{}: {}".format(i+1,X_i))

・実行結果

1: 16807
2: 282475249
3: 1622650073
4: 984943658
5: 1144108930
6: 470211272
7: 101027544
8: 1457850878
9: 1458777923
10: 2007237709
11: 823564440
12: 1115438165
13: 1784484492
14: 74243042
15: 114807987

問題11.3の解答例

例$11.3$と同様な$(p,q)=(5,3)$、$2$ビットの場合の確認を行う。

p,q = 5,3
a = [1, 1, 0, 0, 1]
X, X_10 = [], []

for i in range(2*p-len(a)):
    new_a = (a[len(a)-5]+a[len(a)-3])%2
    a.append(new_a)

for i in range(p):
    X.append(a[2*i:2*(i+1)])
    X_10.append(2*a[2*i]+a[2*i+1])

for i in range(95):
    X_new_0, X_new_1 = (X[len(X)-5][0]-X[len(X)-3][0])%2, (X[len(X)-5][1]-X[len(X)-3][1])%2
    X.append([X_new_0, X_new_1])
    X_10.append(2*X_new_0+X_new_1)

print(X_10[:15])

・実行結果

> print(X_10[:15])
[3, 0, 3, 3, 2, 0, 3, 1, 3, 1, 1, 0, 0, 2, 1]

上記は本文の表$11.4$の結果に一致することが確認できる。

次に$10,000$サンプルを発生させ、適合度検定を行う。

import numpy as np

p,q = 5,3
a = [1, 1, 0, 0, 1, 1, 1, 1, 1, 0]
X, X_10 = [], []
count_X = [0, 0, 0, 0]

for i in range(p):
    X.append(a[2*i:2*(i+1)])
    X_10.append(2*a[2*i]+a[2*i+1])

for i in range(10000):
    X_new_0, X_new_1 = (X[len(X)-5][0]-X[len(X)-3][0])%2, (X[len(X)-5][1]-X[len(X)-3][1])%2
    X.append([X_new_0, X_new_1])
    X_10.append(2*X_new_0+X_new_1)
    count_X[2*X_new_0+X_new_1] += 1

print(X_10[:15])
print(count_X)
print(np.sum((np.array(count_X)-2500.)**2/2500.))

・実行結果

> print(X_10[:15])
[3, 0, 3, 3, 2, 0, 3, 1, 3, 1, 1, 0, 0, 2, 1]
> print(count_X)
[2257, 2583, 2579, 2581]
> print(np.sum((np.array(count_X)-2500.)**2/2500.))
31.496

自由度$4-1=3$の$\chi^2$分布$\chi^2(3)$の上側$5$％点の$\chi^2(3)_{\alpha=0.05}=7.815$であるので、一様性が棄却される。一方で$n=1,000$で同様の操作を行なった場合は$31.496$に対応する値が$2.84$であり、一様性は棄却できない。

問題11.4の解答例

$$
\large
\begin{align}
x_1 &= \sqrt{-2 \log{u_1}} \cdot \cos{(2 \pi u_2)} \quad (11.6)’ \\
x_2 &= \sqrt{-2 \log{u_1}} \cdot \sin{(2 \pi u_2)} \quad (11.6)’
\end{align}
$$

上記は$(11.6)$式の文字を小文字に変換し、取りまとめたものであるが、上記を$u_1$と$u_2$に関して解くことを考える。ここで$x_1^2+x_2^2$と$\displaystyle \frac{x_2}{x_1}$を考えることでそれぞれ下記のように計算できることに着目する。
$$
\large
\begin{align}
x_1^2 + x_2^2 &= (\sqrt{-2 \log{u_1}} \cdot \cos{(2 \pi u_2)})^2 + (\sqrt{-2 \log{u_1}} \cdot \sin{(2 \pi u_2)}) \\
&= -2 \log{u_1} (\cos^{2}{(2 \pi u_2)} + \sin^{2}{(2 \pi u_2)}) \\
&= -2 \log{u_1} \\
\frac{x_2}{x_1} &= \frac{\cancel{\sqrt{-2 \log{u_1}}} \cdot \sin{(2 \pi u_2)}}{\cancel{\sqrt{-2 \log{u_1}}} \cdot \cos{(2 \pi u_2)}} \\
&= \frac{\sin{(2 \pi u_2)}}{\cos{(2 \pi u_2)}} \\
&= \tan{(2 \pi u_2)}
\end{align}
$$

上記を$u_1, u_2$に関して解くと下記が得られる。
$$
\large
\begin{align}
x_1^2 + x_2^2 &= -2 \log{u_1} \\
\log{u_1} &= -\frac{x_1^2+x_2^2}{2} \\
u_1 &= \exp \left( -\frac{x_1^2+x_2^2}{2} \right) \quad (1) \\
\frac{x_2}{x_1} &= \tan{(2 \pi u_2)} \\
2 \pi u_2 &= \tan^{-1}{ \left( \frac{x_2}{x_1} \right) } \\
u_2 &= \frac{1}{2 \pi} \tan^{-1}{ \left( \frac{x_2}{x_1} \right) } \quad (2)
\end{align}
$$

上記の$(1)$式を元に$\displaystyle \frac{\partial u_1}{\partial x_1}, \frac{\partial u_1}{\partial x_2}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial u_1}{\partial x_1} &= \frac{\partial}{\partial x_1} \left( -\frac{x_1^2+x_2^2}{2} \right) \\
&= \exp \left( -\frac{x_1^2+x_2^2}{2} \right) \times \frac{\partial}{\partial x_1} \left( -\frac{x_1^2+x_2^2}{2} \right) \\
&= -x_1 \exp \left( -\frac{x_1^2+x_2^2}{2} \right) = -x_1u_1 \\
\frac{\partial u_1}{\partial x_2} &= \frac{\partial}{\partial x_2} \left( -\frac{x_1^2+x_2^2}{2} \right) \\
&= -x_2 \exp \left( -\frac{x_1^2+x_2^2}{2} \right) = -x_2u_1
\end{align}
$$

また、$(2)$式に対して$\displaystyle (\tan^{-1}{y})’ = \frac{1}{1+y^2}$が成立することを元に、$\displaystyle \frac{\partial u_2}{\partial x_1}, \frac{\partial u_2}{\partial x_2}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial u_2}{\partial x_1} &= \frac{\partial}{\partial x_1} \left( \frac{1}{2 \pi} \tan^{-1}{ \left( \frac{x_2}{x_1} \right) } \right) \\
&= \frac{1}{2 \pi} \frac{1}{\displaystyle 1+\left(\frac{x_2}{x_1}\right)^2} \frac{\partial}{\partial x_1} \left( \frac{x_2}{x_1} \right) \\
&= \frac{1}{2 \pi} \frac{1}{\displaystyle 1+\left(\frac{x_2}{x_1}\right)^2} \left( -\frac{x_2}{x_1^2} \right) \\
&= \frac{1}{2 \pi} \frac{-x_2}{x_1^2+x_2^2} \\
&= -\frac{x_2}{2 \pi(x_1^2+x_2^2)} \\
\frac{\partial u_2}{\partial x_2} &= \frac{\partial}{\partial x_2} \left( \frac{1}{2 \pi} \tan^{-1}{ \left( \frac{x_2}{x_1} \right) } \right) \\
&= \frac{1}{2 \pi} \frac{1}{\displaystyle 1+\left(\frac{x_2}{x_1}\right)^2} \left( \frac{1}{x_1} \right) \\
&= \frac{1}{2 \pi} \frac{1}{\displaystyle 1+\left(\frac{x_2}{x_1}\right)^2} \left( \frac{x_1}{x_1^2} \right) \\
&= \frac{1}{2 \pi} \frac{x_1}{x_1^2+x_2^2} \\
&= \frac{x_1}{2 \pi(x_1^2+x_2^2)}
\end{align}
$$

よって、変数変換におけるヤコビ行列式$|\det J|$は下記のように計算できる。
$$
\large
\begin{align}
|\det J| &= \left| \begin{array}{cc} \displaystyle \frac{\partial u_1}{\partial x_1} & \displaystyle \frac{\partial u_1}{\partial x_2} \\ \displaystyle \frac{\partial u_2}{\partial x_1} & \displaystyle \frac{\partial u_2}{\partial x_2} \end{array} \right| \\
&= \left| \begin{array}{cc} \displaystyle -x_1u_1 & \displaystyle -x_2u_1 \\ \displaystyle -\frac{x_2}{2 \pi(x_1^2+x_2^2)} & \displaystyle \frac{x_1}{2 \pi(x_1^2+x_2^2)} \end{array} \right| \\
&= \left| – \frac{x_1^2u_1}{2 \pi(x_1^2+x_2^2)} – \frac{x_2^2u_1}{2 \pi(x_1^2+x_2^2)} \right| \\
&= \frac{\cancel{(x_1^2+x_2^2)}u_1}{2 \pi \cancel{(x_1^2+x_2^2)}} \\
&= \frac{u_1}{2 \pi}
\end{align}
$$

したがって、$g(x_1,x_2)$に関して下記が得られる。
$$
\large
\begin{align}
g(x_1,x_2) &= f(x_1,x_2) |\det J| \\
&= \frac{u_1}{2 \pi} = \frac{1}{2 \pi} \exp \left( -\frac{x_1^2+x_2^2}{2} \right) \\
&= \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{x_1^2}{2} \right) \times \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{x_2^2}{2} \right)
\end{align}
$$

問題11.5の解答例

下記を実行することで、$X$に$1,000$個の乱数を代入することができる。

a = 11213
M = 2**31-1
X_j = 1
X_ = []

for i in range(1000):
    X_i = 0
    for j in range(12):
        X_j = X_j*a%M
        X_i += X_j/float(M)
    X_.append(X_i-6.)

X = np.array(X_)
print(X[:15])

・実行結果

> print(X[:15])
[-1.83371108 -0.72176246 -1.12172507  0.79117246 -0.89916752 -1.45735712
  1.24864932  0.86215431  0.54254827  0.93210452  0.12854572 -0.33830579
  1.3589318  -0.59776356  0.3665337 ]

ここで得たXに対して問題$5.2$と同じ要領で適合度検定を行うことを考える。

import numpy as np

cumulative = np.array([0., np.sum(X<-3.0), np.sum(X<-2.5), np.sum(X<-2.0), np.sum(X<-1.5), np.sum(X<-1.0), np.sum(X<-0.5), np.sum(X<-0.0), np.sum(X<0.5), np.sum(X<1.0), np.sum(X<1.5), np.sum(X<2.0), np.sum(X<2.5), np.sum(X<3.0), 1000.])
observed = cumulative[1:] - cumulative[:-1]
prob = np.array([0.00135, 0.00486, 0.01654, 0.04406, 0.09185, 0.14988, 0.19146, 0.19146, 0.14988, 0.09185, 0.04406, 0.01654, 0.00486, 0.00135])
estimate = prob*1000

print(estimate)
print((observed-estimate)**2/estimate)
print(np.sum((observed-estimate)**2/estimate))

・実行結果

> print(estimate)
[-1.83371108 -0.72176246 -1.12172507  0.79117246 -0.89916752 -1.45735712
  1.24864932  0.86215431  0.54254827  0.93210452  0.12854572 -0.33830579
  1.3589318  -0.59776356  0.3665337 ]
> print((observed-estimate)**2/estimate)
[ 1.35        0.26740741  2.52307134  1.13126645  0.16137725  0.68330931
  2.40536718  0.82132874  0.02358153  0.2560969   2.71637767  0.01762999
  0.26740741  1.35      ]
> print(np.sum((observed-estimate)**2/estimate))
13.9742211708

上記より$\chi^2 < 14$であり、$\chi^2 < 14 < 22.36… = \chi^2_{\alpha=0.05}(13)$より帰無仮説は棄却できない。

まとめ

Chapter.$11$の「乱数の性質」の演習について取り扱いました。

自然科学の統計学 (基礎統計学)

下記などの内容も参考になると思います。
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html

差分方程式(difference equation)の一般解と隣接三項間漸化式の解法

投稿日: 2022-02-182022-02-18 投稿者: lib-arts

確率過程に関連して差分方程式(difference equation)の一般解などが出てくるが、「数列」で取り扱われる「隣接三項間漸化式」の一般化と考えることもできる。当記事ではどちらの観点からも理解できるように、取りまとめを行なった。
「自然科学の統計学」の10章「確率過程の基礎」の章末の「付節差分方程式の解法」を参考に作成を行なった。

Contents

1 手法の確認
2 演習

手法の確認

問題設定の確認

数列$\{ a_{n} \}$に関して、下記の隣接三項間の漸化式を考える。
$$
\large
\begin{align}
a_{n+2} + p a_{n+1} + q a_{n} = 0, \quad n=0, 1, … \quad (1)
\end{align}
$$

上記は$2$次 or $2$階の差分方程式(difference equation)ともいわれる。これに対し、下記のような特性方程式(characteristic equation)を考える。
$$
\large
\begin{align}
t^2 + p t + q = 0 \quad (2)
\end{align}
$$

この特性方程式の$2$解を$\alpha, \beta$とするとき、$\alpha, \beta$の値に基づいて漸化式の一般項を表すにあたって、以下では導出の確認を行う。

差分方程式(difference equation)の一般解

$$
\large
\begin{align}
a_{n} = \alpha^{n}, \beta^{n}
\end{align}
$$
前項の$\alpha, \beta$に対して、$\alpha \neq \beta$なら上記が漸化式$(1)$の解となる。これに関しては$a_{n+2} = \alpha^{n+2}, a_{n+1} = \alpha^{n+1}, a_{n} = \alpha^{n}$を$(1)$式に代入することで確認できる。
$$
\large
\begin{align}
\alpha^{n+2} + p \alpha^{n+1} + q \alpha^{n} &= \alpha^{n}(\alpha^{2} + p \alpha + q) \\
&= 0
\end{align}
$$

ここで$a_{n} = \alpha^{n}, \beta^{n}$を$1$次数独立な解であると考え、さらに一般的な解を任意の定数$A, B$に関して下記のように考える。
$$
\large
\begin{align}
a_{n} = A \alpha^{n} + B \beta^{n}
\end{align}
$$

上記を漸化式$(1)$の一般解(general solution)という。$A, B$の具体的な値は$a_{0}, a_{1}$などが与えられれば導出できる。$a_{n} = A \alpha^{n} + B \beta^{n}$が解であることは$(1)$式に代入することで、下記のように確認できる。
$$
\large
\begin{align}
a_{n+2} + p a_{n+1} + q a_{n} &= (A \alpha^{n+2} + B \beta^{n+2}) + p (A \alpha^{n+1} + B \beta^{n+1}) + q (A \alpha^{n} + B \beta^{n}) \\
&= A \alpha^{n}(\alpha^{2} + p \alpha + q) + B \beta^{n}(\beta^{2} + p \beta + q) \\
&= 0
\end{align}
$$

ここまでは$\alpha \neq \beta$に関して取り扱ったが、$\alpha = \beta$の重解の場合に関して以下では確認を行う。重解$\alpha$に関しては下記のように一般解を考えることができる。
$$
\large
\begin{align}
a_{n} = (A + Bn) \alpha^{n}
\end{align}
$$

上記の一般解は$a_{n} = n \alpha^{n}$も漸化式$(1)$の解であることからも理解できる。
$$
\large
\begin{align}
(n+2) \alpha^{n+2} + p a_{n+1} + q a_{n} &= n\alpha^{n} (\alpha^{2} + p \alpha + q) \\
&= n\alpha^{n} (\alpha^{2} + p \alpha + q) + 2\alpha^{n+1} \left( \alpha + \frac{p}{2} \right) \\
&= 0
\end{align}
$$
$\displaystyle \alpha + \frac{p}{2} = 0$は$\alpha$が重解であることより導出できる。

隣接三項間漸化式の解法

隣接三項間漸化式の解法も特性方程式の解の$\alpha, \beta$を用いて解を導出する。
・$\alpha \neq \beta$の場合
$$
\large
\begin{align}
a_{n+2} – \alpha a_{n+1} = \beta ( a_{n+1} – \alpha a_{n} ) \\
a_{n+2} – \beta a_{n+1} = \alpha ( a_{n+1} – \beta a_{n} )
\end{align}
$$

上記のように漸化式を変形できることを元に、数列$\{ a_{n+1} – \alpha a_{n} \}$と$\{ a_{n+1} – \beta a_{n} \}$を考える。
・$\{ a_{n+1} – \alpha a_{n} \}$
$$
\large
\begin{align}
a_{n+1} – \alpha a_{n} &= \beta ( a_{n} – \alpha a_{n-1} ) \\
&= … \\
&= \beta^n ( a_{1} – \alpha a_{0} ) \quad (3)
\end{align}
$$

・$\{ a_{n+1} – \beta a_{n} \}$
$$
\large
\begin{align}
a_{n+1} – \beta a_{n} &= \alpha ( a_{n} – \beta a_{n-1} ) \\
&= … \\
&= \alpha^{n} ( a_{1} – \beta a_{0} ) \quad (4)
\end{align}
$$

$\alpha \neq \beta$より、$(3)-(4)$を考える。
$$
\large
\begin{align}
a_{n+1} – \alpha a_{n} – (a_{n+1} – \beta a_{n}) &= \beta^n ( a_{1} – \alpha a_{0} ) – \alpha^{n} ( a_{1} – \beta a_{0} ) \\
(\beta – \alpha) a_{n} &= \beta^n ( a_{1} – \alpha a_{0} ) – \alpha^{n} ( a_{1} – \beta a_{0} ) \\
a_{n} &= \frac{\beta^n ( a_{1} – \alpha a_{0} ) – \alpha^{n} ( a_{1} – \beta a_{0} )}{\beta – \alpha} \quad (5)
\end{align}
$$

ここで$(5)$式に対して、$\displaystyle A = -\frac{a_{1} – \beta a_{0}}{\beta – \alpha}, B = \frac{a_{1} – \alpha a_{0}}{\beta – \alpha}$とおくことで、前項の一般項の式に一致することは抑えておくと良い。

・$\alpha = \beta$の場合
$$
\large
\begin{align}
a_{n+2} – \alpha a_{n+1} = \alpha ( a_{n+1} – \alpha a_{n} )
\end{align}
$$

上記のように漸化式を変形できることを元に、数列${ a_{n+1} – \alpha a_{n} }$を考える。
$$
\large
\begin{align}
a_{n+1} – \alpha a_{n} &= \alpha ( a_{n} – \alpha a_{n-1} ) \\
&= … \\
&= \alpha^n ( a_{1} – \alpha a_{0} ) \quad (6)
\end{align}
$$

ここで$(6)$式の両辺を$\alpha^{n+1}$で割ることで下記のように変形できる。
$$
\large
\begin{align}
a_{n+1} – \alpha a_{n} &= \alpha^n ( a_{1} – \alpha a_{0} ) \\
\frac{a_{n+1}}{\alpha^{n+1}} – \frac{a_{n}}{\alpha^{n}} &= \frac{a_{1} – \alpha a_{0}}{\alpha} \\
\frac{a_{n+1}}{\alpha^{n+1}} &= \frac{a_{n}}{\alpha^{n}} + \frac{a_{1} – \alpha a_{0}}{\alpha}
\end{align}
$$

上記は数列$\displaystyle \left\{ \frac{a_{n}}{\alpha^{n}} \right\}$が等差数列であることを表しており、このことに基づいて下記のように一般項を導出することができる。
$$
\large
\begin{align}
\frac{a_{n}}{\alpha^{n}} &= \frac{a_{n-1}}{\alpha^{n-1}} + \frac{a_{1} – \alpha a_{0}}{\alpha} \\
&= \frac{a_{n-2}}{\alpha^{n-2}} + 2\frac{a_{1} – \alpha a_{0}}{\alpha} \\
&= … \\
&= \frac{a_{0}}{\alpha^{0}} + n\frac{a_{1} – \alpha a_{0}}{\alpha} \\
&= a_{0} + n\frac{a_{1} – \alpha a_{0}}{\alpha} \\
a_{n} &= a_{0} \alpha^{n} + n a_{1} \alpha^{n-1} – n a_{0} \alpha^{n} \\
&= \left( a_{0} + n \left( \frac{a_{1}}{\alpha} – a_{0} \right) \right) \alpha^{n}
\end{align}
$$

ここで$(7)$式に対して、$\displaystyle A = a_{0}, B = \frac{a_{1}}{\alpha} – a_{0}$とおくことで、前項の一般項の式に一致することは抑えておくと良い。

演習

共役事前分布(Conjugate Prior Distribution)まとめ

投稿日: 2022-02-162022-09-30 投稿者: lib-arts

共役事前分布(Conjugate Prior Distribution)はベイズ統計学に基づいてベイズの定理を用いるにあたって計算負荷を減らすことができるので抑えておくと良い。当記事では観測値に仮定される確率分布に対して共役なパラメータの事前分布に関して取りまとめを行なった。
「現代数理統計学」の$14$章「ベイズ法」や、「自然科学の統計学」の$9$章「ベイズ決定」などを参考に作成を行なった。

新装改訂版現代数理統計学

竹村彰通

2,970円(11/09 22:16時点)

自然科学の統計学 (基礎統計学)

Contents

1 共役事前分布の概要
- 1.1 概要
- 1.2 共役事前分布の見つけ方
2 具体的な共役事前分布
3 演習
4 参考

共役事前分布の概要

概要

ベイズ統計ではベイズの定理に基づいて、事後分布$P(\theta|X=x)$を事前分布$P(\theta)$と尤度関数$L(\theta)=f(x|\theta)$の積に基づいて導出する。
$$
\large
\begin{align}
P(\theta|X=x) &= \frac{P(\theta)f(x|\theta)}{P(X=x)} \\
& \propto P(\theta)f(x|\theta)
\end{align}
$$

上記に関して取り扱うにあたっては、事前分布$P(\theta)$と尤度関数$L(\theta)=f(x|\theta)$の関数の形がパラメータ$\theta$に関して同じであればシンプルになることを抑えておくと良い。以下、二項分布とベータ分布を例に詳しく確認を行う。

確率変数$X$が二項分布$Bin(n,p)$に従うとき、パラメータ$p$の事前分布$P(p)$がベータ分布$Be(a,b)$で表されると仮定する。このとき、事前分布$P(p)$と尤度関数$L(p)=f(x|p)$は下記のように表される。
$$
\large
\begin{align}
P(p) &= \frac{1}{B(a,b)} p^{a-1} (1-p)^{b-1} \\
L(p) &= f(x|p) = {}_{n} C_{x} p^{x} (1-p)^{n-x}
\end{align}
$$

このとき、事後分布$P(p|X=x)$は下記のように考えることができる。
$$
\large
\begin{align}
P(p|X=x) & \propto P(\theta)f(x|p) \\
&= \frac{1}{B(a,b)} p^{a-1} (1-p)^{b-1} \times {}_{n} C_{x} p^{x} (1-p)^{n-x} \\
&= \frac{{}_{n} C_{x}}{B(a,b)} p^{a+x-1} (1-p)^{b+n-x-1}
\end{align}
$$
上記より、事後分布$P(p|X=x)$がベータ分布$Be(a+x,b+n-x)$に一致することが確認できる。

ここまでの議論のように、事前分布$P(\theta)$と尤度関数$L(\theta)=f(x|\theta)$をパラメータ$\theta$に関して同様な関数形になるように定めることでベイズの定理の適用にあたっての計算を簡略化することができる。

実用上は尤度関数が先に定められ、その後に事前分布を考えることが多い。上記で確認したような事前分布は共役事前分布(Conjugate Prior Distribution)といわれ、ベイズの定理の適用にあたっての計算を簡略化するにあたって役立てることができる。

共役事前分布の見つけ方

前項で取り扱った「二項分布」と「ベータ分布」のように、確率密度関数に基づく尤度関数をパラメータの関数で見た際に同じ関数形の確率分布がないかを探せば良い。
二項分布の尤度関数の$p$に関する項が$p^{x} (1-p)^{n-x}$で表されることに着目すれば、類似の確率分布は$p^{a-1} (1-p)^{b-1}$で確率密度関数の主要部分が表されるベータ分布が適用できることが推察できる。

ここで確認したような関数形に着目して得られる共役事前分布は、自然共役事前分布(Natural Conjugate Prior Distribution)ともいわれる。

自然共役事前分布(Natural Conjugate Prior Distribution)を用いた事後分布の導出に関しての手順を下記にまとめる。

i) 尤度関数$f(x|\theta)=L(\theta)$をパラメータ$\theta$の関数と見たときに、類似する確率分布がないか探し、事前分布$P(\theta)$を定義する。尤度関数が「二項分布」で表されるときはベータ分布$Be(a,b)$が対応する。
ⅱ) パラメータの事後分布$P(\theta|X)$を尤度関数と事前分布の積から計算する。尤度関数が「二項分布」で表されるときは$P(p|X=x) \propto P(p)f(x|p)$が対応する。
ⅲ) ⅱ)で得られた事後分布$P(\theta|X)$の式から事後分布のパラメータを抜き出し、事前分布と比較する。尤度関数が「二項分布」で表されるときはベータ分布$Be(a,b)$が$Be(a+x,b+n-x)$に更新されることに対応する。

具体的な共役事前分布

二項分布とベータ分布

「共役事前分布の概要」の具体例で確認を行なったので省略する。

正規分布

確率変数$X$が正規分布$N(\mu,\sigma^2)$に従うとき、パラメータ$\mu$の事前分布$P(\mu)$が正規分布$N(\lambda,\tau^2)$で表されると仮定する。このとき、事前分布$P(\mu)$と尤度関数$L(\mu)=f(x_1,…,x_n|\mu)$は下記のように表される。
$$
\large
\begin{align}
P(\mu) &= \frac{1}{\sqrt{2 \pi}\tau} \exp \left[ -\frac{(\mu-\lambda)^2}{2 \tau^2} \right] \\
L(\mu) &= f(x_1,…,x_n|\mu) = \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi}\sigma} \exp \left[ -\frac{(x_i-\mu)^2}{2 \sigma^2} \right] \\
&= \left( \frac{1}{\sqrt{2 \pi}\sigma} \right)^{n} \exp \left[ – \frac{1}{2 \sigma^2}\sum_{i=1}^{n} (x_i-\mu)^2 \right] \\
&= \left( \frac{1}{\sqrt{2 \pi}\sigma} \right)^{n} \exp \left[ – \frac{1}{2 \sigma^2}\sum_{i=1}^{n} \left( (x_i-\bar{x})^2 + (\bar{x}-\mu)^2 + 2(x_i-\bar{x})(\bar{x}-\mu) \right) \right] \\
&= \exp \left[ – \sum_{i=1}^{n} \frac{(\bar{x}-\mu)^2}{2 \sigma^2} \right] \left( \frac{1}{\sqrt{2 \pi}\sigma} \right)^{n} \exp \left[ – \frac{1}{2 \sigma^2}\sum_{i=1}^{n} (x_i – \bar{x})^2 + 2(\bar{x}-\mu)\sum_{i=1}^{n}(x_i-\bar{x}) \right] \\
&= \exp \left[ – \frac{n(\mu-\bar{x})^2}{2 \sigma^2} \right] \left( \frac{1}{\sqrt{2 \pi}\sigma} \right)^{n} \exp \left[ – \frac{1}{2 \sigma^2}\sum_{i=1}^{n} (x_i – \bar{x})^2 \right]
\end{align}
$$

このとき、事後分布$P(\mu|X=x_1,…,x_n)$は下記のように考えることができる。
$$
\large
\begin{align}
P(\mu|X=x_1,…,x_n) & \propto P(\mu)f(x_1,…,x_n|\mu) \\
& \propto \exp \left[ -\frac{(\mu-\lambda)^2}{2 \tau^2} \right] \times \exp \left[ – \frac{n(\mu-\bar{x})^2}{2 \sigma^2} \right] \\
&= \exp \left[ -\frac{\sigma^2(\mu-\lambda)^2 + n \tau^2(\mu-\bar{x})^2}{2 \sigma^2 \tau^2} \right] \\
&= \exp \left[ -\frac{(n \tau^2 + \sigma^2)\mu^2 – 2(n \tau^2 \bar{x} + \sigma^2 \lambda)\mu + …}{2 \sigma^2 \tau^2} \right] \\
& \propto \exp \left[ -\frac{n \tau^2 + \sigma^2}{2 \sigma^2 \tau^2} \left(\mu – \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} \right)^2 \right]
\end{align}
$$

ここまでの議論により、$\mu$に関する事前分布$N(\lambda,\tau^2)$が、$N(\mu,\sigma^2)$に基づく観測値$x_1,…,x_n$を用いて、事後分布$\displaystyle N \left( \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} , \frac{\sigma^2 \tau^2}{n \tau^2 + \sigma^2} \right)$を得ることができる。

ポアソン分布とガンマ分布

確率変数$X$がポアソン分布$Po(\lambda)$に従うとき、パラメータ$\lambda$の事前分布$P(\lambda)$がガンマ分布$Ga(a,1)$で表されると仮定する。このとき、事前分布$P(\lambda)$と尤度関数$L(\lambda)=f(x_1,…,x_n|\lambda)$は下記のように表される。
$$
\large
\begin{align}
P(\lambda) &= \frac{1}{\Gamma(a)} \lambda^{a-1} e^{-\lambda} \\
L(\lambda) &= f(x_1,…,x_n|\lambda) = \prod_{i=1}^{n} \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \\
&= \lambda^{\sum_{i=1}^{n} x_i} e^{-n \lambda} \prod_{i=1}^{n} \frac{1}{x_i!} \\
&= \lambda^{n \bar{x}} e^{-n \lambda} \prod_{i=1}^{n} \frac{1}{x_i!}
\end{align}
$$

このとき、事後分布$P(\lambda|X=x_1,…,x_n)$は下記のように考えることができる。
$$
\large
\begin{align}
P(\lambda|X=x_1,…,x_n) & \propto P(\lambda)f(x_1,…,x_n|\lambda) \\
&= \frac{1}{\Gamma(a)} \lambda^{a-1} e^{-\lambda} \times \lambda^{n \bar{x}} e^{-n \lambda} \prod_{i=1}^{n} \frac{1}{x_i!} \\
& \propto \lambda^{a + n \bar{x} – 1} e^{-(n+1)\lambda} \\
\end{align}
$$
ここまでの議論により、$\lambda$に関する事前分布$Ga(a,1)$が、$Po(\lambda)$に基づく観測値$x_1,…,x_n$を用いて、事後分布$Ga(a + n \bar{x}, n+1)$を得ることができる。

さらに、ガンマ分布$Ga(a,b)$の期待値が$\displaystyle \frac{a}{b}$、分散が$\displaystyle \frac{a}{b^2}$であることから、事前分布$Ga(a,1)$と事後分布$Ga(a + n \bar{x}, n+1)$の期待値$E[\lambda], E[\lambda|x_1,…,x_n]$と分散$V[\lambda], V[\lambda|x_1,…,x_n]$はそれぞれ下記のように得られる。
$$
\large
\begin{align}
E[\lambda] &= a \\
E[\lambda|x_1,…,x_n] &= \frac{a + n \bar{x}}{n+1} \\
V[\lambda] &= a \\
V[\lambda|x_1,…,x_n] &= \frac{a + n \bar{x}}{(n+1)^2}
\end{align}
$$

上記より、$n$が大きくなるにつれて、$E[\lambda|x_1,…,x_n]$が$\bar{x}$に近づくことと、$V[\lambda|x_1,…,x_n]$が$0$に近づくことが確認できる。

ガンマ分布の期待値や分散に関しては下記で詳しく取り扱った。ここでの$b$に対して$\displaystyle b = \frac{1}{\alpha}$のように置き換えられていることに注意。
https://www.hello-statisticians.com/explain-terms-cat/gamma_distribution1.html

演習

「二項分布」と「ベータ分布」に関する演習を下記で取り扱った。
https://www.hello-statisticians.com/practice/stat_practice20.html#i-3

新装改訂版現代数理統計学

竹村彰通

2,970円(11/09 22:16時点)

自然科学の統計学 (基礎統計学)

参考

（YouTube）【ゲーム×統計＠桃鉄】# 04 勝率を推論しよう（ベイズ推論を使う）
- プレーヤーの勝敗結果がカテゴリ分布（多項分布の特殊形）に従うと仮定し、パラメータをベイズ推定する
（YouTube）カテゴリ分布のパラメータを推論する（前半）
（YouTube）カテゴリ分布のパラメータを推論する（後半）
- カテゴリ分布（多項分布の特殊形）のパラメータのベイズ推論について解説

Ch.7 「分布の仮定」の章末問題の解答例　〜基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)〜

投稿日: 2022-02-142022-09-07 投稿者: lib-arts

当記事は「基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)」の読解サポートにあたってChapter.$7$の「分布の仮定」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

自然科学の統計学 (基礎統計学)

Contents

1 章末の演習問題について
2 まとめ

章末の演習問題について

問題7.1の解答例

問題7.2の解答例

i)
$$
\large
\begin{align}
L(\theta) = \sum_{i=1}^{n} (X_i-\theta)^2
\end{align}
$$
上記のような$L(\theta)$が与えられたとき、$L(\theta)$を最小にする$\theta$を考える。

ここで$L(\theta)$を$\theta$で微分すると下記が得られる。
$$
\large
\begin{align}
\frac{\partial L(\theta)}{\partial \theta} &= -2 \sum_{i=1}^{n} (X_i-\theta) \\
&= -2 (n \bar{X} – n \theta) \\
&= 2n (\theta – \bar{X})
\end{align}
$$

上記は$\theta$の単調増加関数であることから、$L(\theta)$を最小にする$\theta$は$\bar{X}$であることがわかる。

問題7.3の解答例

下記のPython実装のような計算を行うことで、結果を計算することができる。

import numpy as np

x = np.array([8.2,7.5,8.7,8.4,9.6])
theta = 8.4
for i in range(10):
    W = 1/(1+(x-theta)**2)
    theta = np.sum(W*x)/np.sum(W)
    print(theta)

・実行結果

8.42017221731
8.42650412892
8.42849591517
8.42912290722
8.42932032277
8.42938248582
8.42940206044
8.42940822436
8.42941016535
8.42941077656

問題7.4の解答例

i)
観測値は下記のように幹葉表示することができる。
$$
\large
\begin{array}{|c|*3{c|}}\hline \mathrm{stem} & \mathrm{leaf} & \mathrm{degree} & \mathrm{depth} : n=25 \\
\hline 5.5 & 77 & 2 & 2 \\
\hline 5.2 & 5 & 1 & 3 \\
\hline 5.1 & 233689 & 6 & 9 \\
\hline 5.0 & 112458 & 6 & \\
\hline 4.9 & 058 & 3 & 10 \\
\hline 4.8 & 0117 & 4 & 7 \\
\hline 4.7 & 9 & 1 & 3 \\
\hline 4.6 & 9 & 1 & 2 \\
\hline 4.5 & 8 & 1 & 1 \\
\hline
\end{array}
$$

ⅱ)
下記のPythonを実行することで平均$\bar{X}$が得られる。

import numpy as np

x = np.array([4.95,5.02,5.08,4.90,5.12,5.19,4.80, \
4.87,4.98,4.58,4.81,5.18,5.25,5.05,4.79,5.57,5.01, \
5.57,5.01,4.81,5.13,5.04,5.13,5.16,4.69])

print(np.sum(x)/25.)

・実行結果

5.0276

ⅲ)
i)で表した幹葉表示より、$X_{med}=5.02$であることが確認できる。

iv)
下記のPythonを実行することで$k=3$のトリム平均$\hat{\theta}_{trim}(3)$が得られる。

import numpy as np

x = np.array([4.95,5.02,5.08,4.90,5.12,5.19,4.80, \
4.87,4.98,4.58,4.81,5.18,5.25,5.05,4.79,5.57,5.01, \
5.57,5.01,4.81,5.13,5.04,5.13,5.16,4.69])

print(np.sum(np.sort(x)[3:-3])/(25.-6.))

・実行結果

5.0126...

vi)

問題7.5の解答例

$(7.33), (7.34)$式を元に二項分布$Bin(17,0.5)$を考えると、棄却域が$N \leq 4, 13 \leq N$のときに有意水準が$\alpha=0.0490 \simeq 0.05$となる。ここで与えられた観測値は$N=5$であるので、「母平均$=0$」の帰無仮説は棄却されない。

問題7.6の解答例

下記のように$2$つの標本を小さいものから順に並べることができる。第$2$標本の方が数が少ないので第$2$標本を元に考えるにあたって、第$2$標本の観測値には下線を引いた。
$$
\large
\begin{align}
& 42.6, 43.9, 44.1, 44.2, \underline{44.7}, 45.0, 45.8, \underline{46.8}, \underline{46.9}, \underline{47.1}, \\
& 47.4, 48.0, \underline{48.2}, 48.7, 49.5, 49.6, \underline{50.0}, 50.0, 51.4, \underline{52.1}, \\
& 52.7, 52.8, \underline{53.5}, \underline{54.2}, \underline{56.3}
\end{align}
$$

上記より、第$2$標本の各観測値の順位はそれぞれ下記のように表される。
$$
\large
\begin{align}
5, 8, 9, 10, 13, 17.5, 20, 23, 24, 25
\end{align}
$$

従って、順位和$W$は$W=154.5$となる。本文の表$7.2$より、両側$5％$の棄却域は$94$以下または$m(m+n+1)-94=10(10+15+1)-94=166$以上である。よって、「二つの平均が等しい」と考える帰無仮説は棄却できない。

問題7.7の解答例

i)
下記を実行することで正規確率紙へのプロットを行うことができる。

import numpy as np
import matplotlib.pyplot as plt

x_A = np.array([10.5, 10.4, 10.6, 11.9, 11.3, 11.8, 11.7, 12.6, 10.9, 11.1, 13.0, 11.2, 13.4, 10.8, 11.2])
x_B = np.array([20.0, 18.3, 20.3, 37.1, 20.2, 21.0, 6.5, 24.0, 14.2, 21.0, 18.3, 13.4, 14.8, 21.6, 16.8])

x_A_ranked = np.sort(x_A)
x_B_ranked = np.sort(x_B)
y = np.linspace(0.,1.,16)

plt.subplot(121)
plt.plot(x_A_ranked,y[1:])
plt.yscale("log")
plt.ylim([0.06,1.01])
plt.subplot(122)
plt.plot(x_B_ranked,y[1:])
plt.yscale("log")
plt.ylim([0.06,1.01])
plt.show()

・実行結果

ⅱ)
下記を実行することで$b_1, b_2$の計算を行うことができる。

def calc_moment(x):
    m2 = np.sum((x-np.mean(x))**2)/x.shape[0]
    m3 = np.sum((x-np.mean(x))**3)/x.shape[0]
    m4 = np.sum((x-np.mean(x))**4)/x.shape[0]
    b1 = m3/(m2)**(1.5)
    b2 = m4/m2**2 - 3.
    return b1, b2

b1_A, b2_A = calc_moment(x_A)
b1_B, b2_B = calc_moment(x_B)

print("・A")
print("b1: {:.2f}, b2: {:.2f}".format(b1_A,b2_A))
print("===")
print("・B")
print("b1: {:.2f}, b2: {:.2f}".format(b1_B,b2_B))

・実行結果

・A
b1: 0.80, b2: -0.40
===
・B
b1: 0.90, b2: 2.40

ここで$n=15$のときの$5％$点が$b_1=0.9, b_2=1.1$、$1$％点が$b_1=1.3, b_2=2.3$であることから、$A$は$5$％でも棄却できず、$B$は$1$％で棄却できることが確認される。よって、$B$は正規分布に従っていないと考えられる。

まとめ

Ch.9 「ベイズ決定」の章末問題の解答例　〜基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)〜

投稿日: 2022-02-122022-08-07 投稿者: lib-arts

当記事は「基礎統計学Ⅲ 自然科学の統計学(東京大学出版会)」の読解サポートにあたってChapter.$9$の「ベイズ決定」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

自然科学の統計学 (基礎統計学)

Contents

1 章末の演習問題について
2 まとめ

章末の演習問題について

問題9.1の解答例

巻末の解答を確認したところ、つぼ$H_3$のSとFの比例が$2:1$ではなく、$1:2$で計算していると思われるので、以下では巻末の解答に合わせて$S:F=1:2$で計算を行う。

i)
$$
\large
\begin{align}
P(H_i|S) = \frac{P(H_i)P(S|H_i)}{P(S)}
\end{align}
$$
上記のベイズの定理の式に従って計算を行う。ここで$\displaystyle H_i = \frac{1}{3}, P(S) = \sum_{i=1}^{3} P(H_i)P(S|H_i)$より、$P(S)$の計算を行う。
$$
\large
\begin{align}
P(S) &= \sum_{i=1}^{3} P(H_i)P(S|H_i) \\
&= \frac{1}{3} \sum_{i=1}^{3} P(S|H_i) \\
&= \frac{1}{3} \left( \frac{3}{4} + \frac{1}{2} + \frac{1}{3} \right) \\
&= \frac{1}{3} \times \frac{9+6+4}{12} \\
&= \frac{19}{36}
\end{align}
$$

このとき、$P(H_1|S), P(H_2|S), P(H_3|S)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
P(H_1|S) &= \frac{P(H_1)P(S|H_1)}{P(S)} \\
&= \frac{1}{3} \times \frac{3}{4} \times \frac{36}{19} \\
&= \frac{9}{19} \\
P(H_2|S) &= \frac{P(H_2)P(S|H_2)}{P(S)} \\
&= \frac{1}{3} \times \frac{1}{2} \times \frac{36}{19} \\
&= \frac{6}{19} \\
P(H_3|S) &= \frac{P(H_3)P(S|H_3)}{P(S)} \\
&= \frac{1}{3} \times \frac{1}{3} \times \frac{36}{19} \\
&= \frac{4}{19}
\end{align}
$$

ⅱ)
$$
\large
\begin{align}
P(H_i|S_1,S_2) = \frac{P(H_i|S_1)P(S_2|H_i,S_1)}{P(S_1,S_2)}
\end{align}
$$
上記のベイズの定理の式に従って計算を行う。ここで$\displaystyle P(S_1,S_2) = \sum_{i=1}^{3} P(H_i|S_1)P(S_2|H_i,S_1)$より、$P(S_1,S_2)$の計算を行う。
$$
\large
\begin{align}
P(S_1,S_2) &= \sum_{i=1}^{3} P(H_i|S_1)P(S_2|H_i,S_1) \\
&= \frac{9}{19} \times \frac{3}{4} + \frac{6}{19} \times \frac{1}{2} + \frac{6}{19} \times \frac{1}{3} \\
&= \frac{9 \times 3 \times 3 + 6 \times 6 + 4 \times 4}{19 \times 4 \times 3} = \frac{133}{228}
\end{align}
$$

このとき、$P(H_1|S_1,S_2), P(H_2|S_1,S_2), P(H_3|S_1,S_2)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
P(H_1|S_1,S_2) &= \frac{P(H_1|S_1)P(S_2|H_1,S_1)}{P(S_1,S_2)} \\
&= \frac{9}{19} \times \frac{3}{4} \times \frac{228}{133} \\
&= \frac{81}{133} \\
P(H_2|S_1,S_2) &= \frac{P(H_2|S_1)P(S_2|H_2,S_1)}{P(S_1,S_2)} \\
&= \frac{6}{19} \times \frac{1}{2} \times \frac{228}{133} \\
&= \frac{36}{133} \\
P(H_3|S_1,S_2) &= \frac{P(H_3|S_1)P(S_2|H_3,S_1)}{P(S_1,S_2)} \\
&= \frac{4}{19} \times \frac{1}{3} \times \frac{228}{133} \\
&= \frac{16}{133}
\end{align}
$$

ⅲ)
$$
\large
\begin{align}
P(H_i|S_1,S_2) = \frac{P(H_i)P(S_1,S_2|H_i)}{P(S_1,S_2)}
\end{align}
$$
上記のベイズの定理の式に従って計算を行う。ここで$\displaystyle P(S_1,S_2) = \sum_{i=1}^{3} P(H_i)P(S_1,S_2|H_i)$より、$P(S_1,S_2)$の計算を行う。
$$
\large
\begin{align}
P(S_1,S_2) &= \sum_{i=1}^{3} P(H_i)P(S_1,S_2|H_i) \\
&= \frac{1}{3} \times \left( \frac{3}{4} \right)^2 + \frac{1}{3} \times \left( \frac{1}{2} \right)^2 + \frac{1}{3} \times \left( \frac{1}{3} \right)^2 \\
&= \frac{3^2 \times 3^2 + 4 \times 3^2 + 4^2}{3^3 \times 4^2} = \frac{133}{3^3 \times 4^2}
\end{align}
$$

このとき、$P(H_1|S_1,S_2), P(H_2|S_1,S_2), P(H_3|S_1,S_2)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
P(H_1|S_1,S_2) &= \frac{P(H_1)P(S_1,S_2|H_1)}{P(S_1,S_2)} \\
&= \frac{1}{3} \times \left( \frac{3}{4} \right)^2 \times \frac{3^3 \times 4^2}{133} \\
&= \frac{81}{133} \\
P(H_2|S_1,S_2) &= \frac{P(H_2)P(S_1,S_2|H_2)}{P(S_1,S_2)} \\
&= \frac{1}{3} \times \left( \frac{1}{2} \right)^2 \times \frac{3^3 \times 4^2}{133} \\
&= \frac{36}{133} \\
P(H_3|S_1,S_2) &= \frac{P(H_3)P(S_1,S_2|H_3)}{P(S_1,S_2)} \\
&= \frac{1}{3} \times \left( \frac{1}{3} \right)^2 \times \frac{3^3 \times 4^2}{133} \\
&= \frac{16}{133}
\end{align}
$$

問題9.2の解答例

$P(S)=P(S_1,S_2)$は下記のように計算することができる。
$$
\large
\begin{align}
P(S) &= P(S_1,S_2) = \sum_{i=1}^{3} P(H_i|S_1)P(S_2|H_i,S_1) \\
&= \frac{9}{19} \times \frac{3}{4} + \frac{6}{19} \times \frac{1}{2} + \frac{6}{19} \times \frac{1}{3} \\
&= \frac{9 \times 3 \times 3 + 6 \times 6 + 4 \times 4}{19 \times 4 \times 3} = \frac{133}{228}
\end{align}
$$

また、同様に$P(F)=P(S_1,F_2)$は下記のように計算することができる。
$$
\large
\begin{align}
P(F) &= P(S_1,F_2) = \sum_{i=1}^{3} P(H_i|S_1)P(F_2|H_i,S_1) \\
&= \frac{9}{19} \times \frac{1}{4} + \frac{6}{19} \times \frac{1}{2} + \frac{6}{19} \times \frac{2}{3} \\
&= \frac{9 \times 3 + 6 \times 6 + 4 \times 2 \times 4}{19 \times 4 \times 3} = \frac{95}{228} = 1 – P(S_1,S_2)
\end{align}
$$

問題9.3の解答例

$5$回目の試行の後の$\theta$の事後確率分布が$Be(5,2)$であることから、$\theta$の期待値は下記のように計算できる。
$$
\large
\begin{align}
\int_{0}^{1} \theta \times \frac{1}{B(5,2)} \theta^{5-1} (1-\theta)^{2-1} dx &= \frac{(5+2-1)!}{(5-1)!(2-1)!} \int_{0}^{1} \theta^{5} (1-\theta) dx \\
&= 5 \times 6 \times \left[ \frac{1}{6}\theta^6 – \frac{1}{7}\theta^7 \right]_{0}^{1} \\
&= \frac{5 \times 6}{6 \times 7} = \frac{5}{7}
\end{align}
$$

問題9.4の解答例

https://www.hello-statisticians.com/explain-terms-cat/conjugate_dist1.html#i-6
上記の導出結果の事後分布$\displaystyle N \left( \frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} , \frac{\sigma^2 \tau^2}{n \tau^2 + \sigma^2} \right)$に対して値を代入することで結果を得ることができる。
$$
\large
\begin{align}
\frac{n \tau^2 \bar{x} + \sigma^2 \lambda}{n \tau^2 + \sigma^2} &= \frac{1 \times 1/2 \times 6.5 + 1/4 \times 5}{1 \times 1/2 + 1/4} \\
&= \frac{2 \times 6.5 + 5}{2 + 1} \\
&= 6 \\
\frac{\sigma^2 \tau^2}{n \tau^2 + \sigma^2} &= \frac{1/4 \times 1/2}{1 \times 1/2 + 1/4} \\
&= \frac{1}{4+2} \\
&= \frac{1}{6}
\end{align}
$$

巻末の解答とは平均の値が異なるが、巻末の解答はおそらく計算ミスだと思われた。

問題9.5の解答例

i)
事後確率$P(D|S=(1,1,0)), P(\bar{D}|S=(1,1,0))$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
P(D|S=(1,1,0)) &= \frac{P(D)P(S=(1,1,0)|D)}{P(S=(1,1,0))} \\
&= \frac{P(D)P(S=(1,1,0)|D)}{P(D)P(S=(1,1,0)|D) + P(\bar{D})P(S=(1,1,0)|\bar{D})} \\
&= \frac{P(D)P(S_1=1|D)P(S_2=1|D)P(S_3=0|D)}{P(D)P(S_1=1|D)P(S_2=1|D)P(S_3=0|D) + P(\bar{D})P(S_1=1|\bar{D})P(S_2=1|\bar{D})P(S_3=0|\bar{D})} \\
&= \frac{0.23 \times 0.1 \times 0.7 \times (1-0.6)}{0.23 \times 0.1 \times 0.7 \times (1-0.6) + 0.77 \times 0.8 \times 0.2 \times (1-0.5)} \\
&= 0.0946… \simeq 0.095 \\
P(\bar{D}|S=(1,1,0)) &= \frac{P(\bar{D})P(S_1=1|\bar{D})P(S_2=1|\bar{D})P(S_3=0|\bar{D})}{P(D)P(S_1=1|D)P(S_2=1|D)P(S_3=0|D) + P(\bar{D})P(S_1=1|\bar{D})P(S_2=1|\bar{D})P(S_3=0|\bar{D})} \\
&= \frac{0.77 \times 0.8 \times 0.2 \times (1-0.5)}{0.23 \times 0.1 \times 0.7 \times (1-0.6) + 0.77 \times 0.8 \times 0.2 \times (1-0.5)} \\
&= 0.9053… \simeq 0.905
\end{align}
$$

問題9.6の解答例

i)
晴天と雨天の事前確率がそれぞれ$\displaystyle \frac{1}{2}$のとき、損失の期待値が最小となるのは$a_2$であるので、$a_2$が最適な行動となる。また、事前確率を$p, 1-p$とおくときは、$a_1,a_2,a_3$それぞれの損失の期待値$E[L(a_1)],E[L(a_2)],E[L(a_3)]$は下記のように計算できる。
$$
\large
\begin{align}
E[L(a_1)] &= p \times 0 + (1-p) \times 5 \\
&= 5(1-p) \\
E[L(a_2)] &= p \times 1 + (1-p) \times 3 \\
&= p + 3(1-p) \\
E[L(a_3)] &= p \times 3 + (1-p) \times 2 \\
&= 3p + 2(1-p)
\end{align}
$$

以下、$E[L(a_1)] < E[L(a_2)], E[L(a_2)] < E[L(a_3)]$を$p$について解き、最適な行動を調べる。・$E[L(a_1)] < E[L(a_2)]$
$$
\large
\begin{align}
E[L(a_1)] &< E[L(a_2)]　\\
5(1-p) &< p + 3(1-p) \\
2(1-p) &< p \\
2 &< 3p \\
p &> \frac{2}{3}
\end{align}
$$

・$E[L(a_2)] < E[L(a_3)]$
$$
\large
\begin{align}
E[L(a_2)] &< E[L(a_3)] \\
p + 3(1-p) &< 3p + 2(1-p) \\
1-p &< 2p \\
1 &< 3p \\
p &> \frac{1}{3}
\end{align}
$$

ここまでの議論により、$p$が$\displaystyle \left[ 0,\frac{1}{3} \right)$の時は$a_3$、$\displaystyle \left[ \frac{1}{3},\frac{2}{3} \right)$の時は$a_2$、$\displaystyle \left[ \frac{2}{3},1 \right]$の時は$a_1$がそれぞれ最適な行動となる。

ⅱ)
$$
\large
\begin{align}
P(\theta_1|z_i) &= \frac{P(\theta_1)P(z_i|\theta_1)}{P(z_i)} \\
&= \frac{P(\theta_1)P(z_i|\theta_1)}{P(\theta_1)P(z_i|\theta_1)+P(\theta_2)P(z_i|\theta_2)} \\
P(\theta_2|z_i) &= 1 – P(\theta_1|z_i)
\end{align}
$$
事後確率はベイズの定理や補集合の活用により、上記のように計算することができる。巻末の解答では事前確率に関して$\displaystyle P(\theta_1)=\frac{1}{2}, P(\theta_2)=\frac{1}{2}$を設定しているので、以下ではこの前提で計算を行う。

・$z_1$
$$
\large
\begin{align}
P(\theta_1|z_1) &= \frac{P(\theta_1)P(z_1|\theta_1)}{P(\theta_1)P(z_1|\theta_1)+P(\theta_2)P(z_1|\theta_2)} \\
&= \frac{0.5 \times 0.60}{0.5 \times 0.60 + 0.5 \times 0.20} = \frac{3}{4} \\
P(\theta_2|z_1) &= 1 – P(\theta_1|z_1) = \frac{1}{4}
\end{align}
$$

・$z_2$
$$
\large
\begin{align}
P(\theta_1|z_2) &= \frac{P(\theta_1)P(z_2|\theta_1)}{P(\theta_1)P(z_2|\theta_1)+P(\theta_2)P(z_2|\theta_2)} \\
&= \frac{0.5 \times 0.25}{0.5 \times 0.25 + 0.5 \times 0.30} = \frac{5}{11} \\
P(\theta_2|z_2) &= 1 – P(\theta_1|z_2) = \frac{6}{11}
\end{align}
$$

・$z_3$
$$
\large
\begin{align}
P(\theta_1|z_3) &= \frac{P(\theta_1)P(z_3|\theta_1)}{P(\theta_1)P(z_3|\theta_1)+P(\theta_2)P(z_3|\theta_2)} \\
&= \frac{0.5 \times 0.25}{0.5 \times 0.15 + 0.5 \times 0.50} = \frac{3}{13} \\
P(\theta_2|z_1) &= 1 – P(\theta_1|z_1) = \frac{10}{13}
\end{align}
$$

ⅲ)
i)の結果に基づき、$z_1$の時は$a_1$、$z_2$の時は$a_2$、$z_3$の時は$a_3$がそれぞれ最適な行動となる。

問題9.7の解答例

問題9.8の解答例

問題9.9の解答例

まとめ

Chapter.$9$の「ベイズ決定」の演習について取り扱いました。

自然科学の統計学 (基礎統計学)

統計検定3級問題解説～2018年11月実施～（問11～問18）

投稿日: 2022-02-122022-02-27 投稿者: ryoukom

Contents

1 過去問題
2 問11 解答
3 問12 解答
4 問13 解答
5 問14 解答
6 問15 解答
7 問16 解答
8 問17 解答
9 問18 解答
10 問19 解答

過去問題

過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。

統計検定3級（2018.11）【問題】（統計検定公式）＜※期間限定＞
統計検定3級（2018.11）【正解】（統計検定公式）

日本統計学会公式認定統計検定 3級・4級公式問題集［2018〜2021年］

1,980円(11/09 16:42時点)