数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事ではポアソン分布、正規分布、指数分布などの確率分布の確率密度関数とパラメータの対応やグラフの描画に関して取り扱いました。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
離散型確率分布
ポアソン分布
$$
\large
\begin{align}
f(x|\lambda) = \frac{\lambda^{x} e^{-\lambda}}{x!}, \quad x \geq 0
\end{align}
$$
上記で表したポアソン分布$Po(\lambda)$の確率密度関数のグラフは下記を実行することで描画を行うことができる。
import math
import matplotlib.pyplot as plt
import numpy as np
def factorial(vec):
res = np.zeros(vec.shape[0])
for i in range(vec.shape[0]):
res[i] = math.factorial(vec[i])
return res
lamb1, lamb2, lamb3 = 3., 5., 7.
x = np.arange(0, 16, 1)
y1 = lamb1**x * np.e**(-lamb1) / factorial(x)
y2 = lamb2**x * np.e**(-lamb2) / factorial(x)
y3 = lamb3**x * np.e**(-lamb3) / factorial(x)
plt.plot(x,y1,color="blue",label="lambda: {:.1f}".format(lamb1))
plt.plot(x,y2,color="green",label="lambda: {:.1f}".format(lamb2))
plt.plot(x,y3,color="red",label="lambda: {:.1f}".format(lamb3))
plt.legend()
plt.show()・実行結果
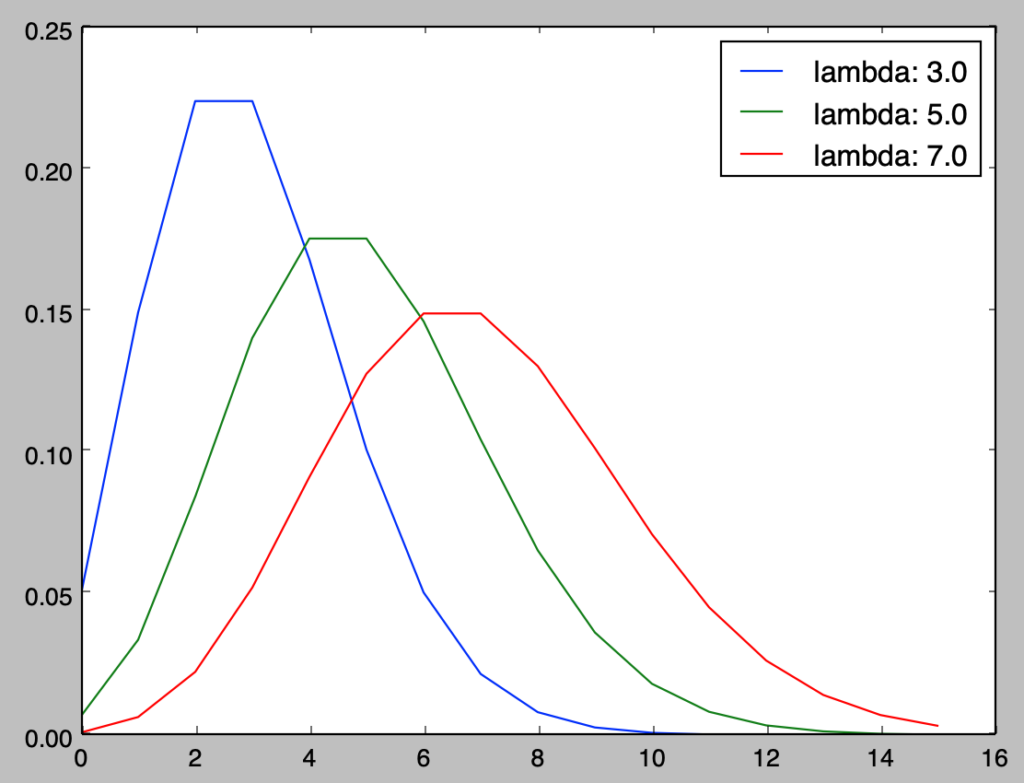
連続型確率分布
正規分布
$$
\large
\begin{align}
f(x|\mu,\sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left[ -\frac{(x-\mu)^2}{2 \sigma^2} \right]
\end{align}
$$
上記で表した正規分布$N(\mu,\sigma)$の確率密度関数のグラフは下記を実行することで描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
mu = 0
sigma = np.array([0.5, 1., 2.])
x = np.arange(-5., 5.01, 0.01)
for i in range(sigma.shape[0]):
y = np.exp(-(x-mu)**2/(2*sigma[i]**2))/np.sqrt(2*np.pi*sigma[i]**2)
plt.plot(x,y,label="mu: {:.1f}, sigma: {:.1f}".format(mu,sigma[i]))
plt.legend()
plt.show()・実行結果
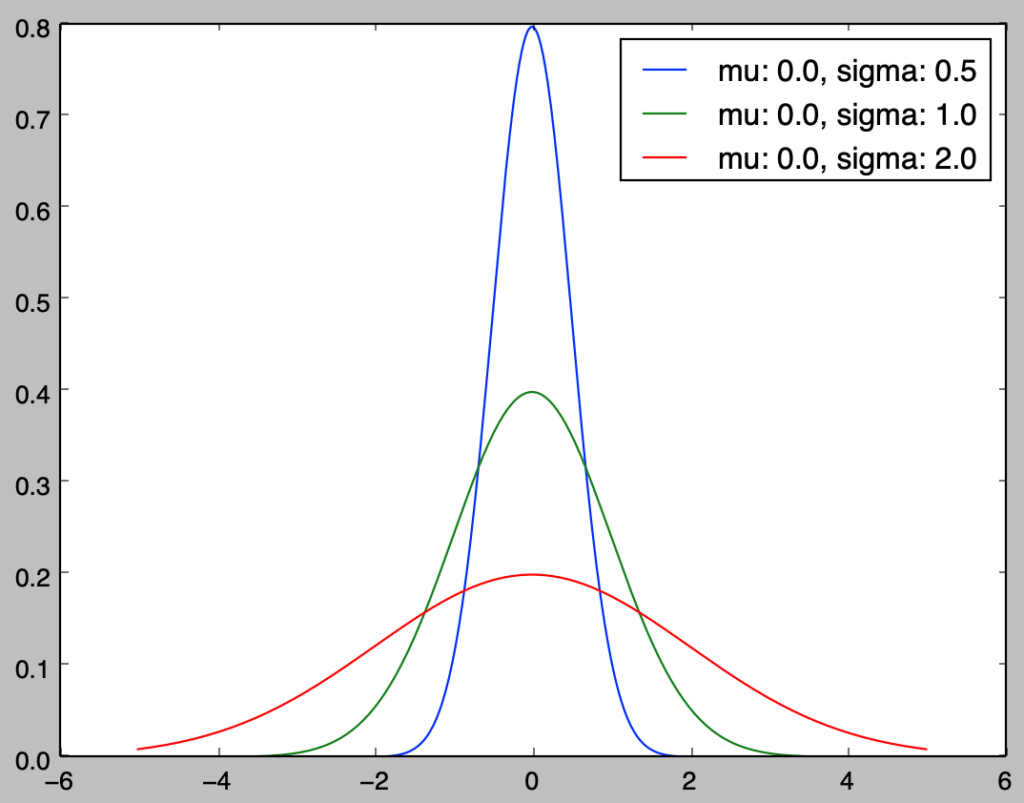
指数分布
$$
\large
\begin{align}
f(x|\lambda) = \lambda e^{-\lambda x}, \quad x \geq 0
\end{align}
$$
上記で表した正規分布$Exp(\lambda)$の確率密度関数のグラフは下記を実行することで描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
lamb = np.array([0.5, 1., 2.])
x = np.arange(0., 5.01, 0.01)
for i in range(lamb.shape[0]):
y = lamb[i] * np.e**(-lamb[i]*x)
plt.plot(x,y,label="lambda: {:.1f}".format(lamb[i]))
plt.legend()
plt.show()・実行結果
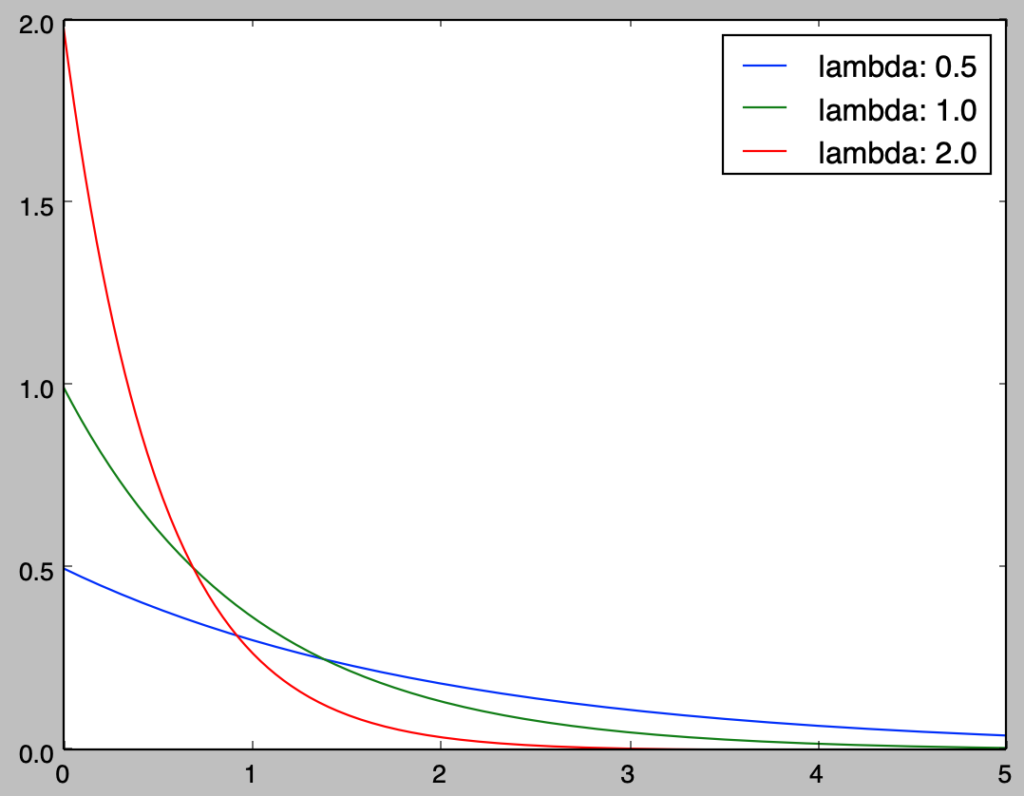

[…] Pythonを用いた確率分布のプログラミング 〜ポアソン分布、正規分布、指数… […]