有限マクローリン展開(finite maclaurin expansion)は有限テイラー展開の特殊な場合であり、近似値の計算などに用いることができます。当記事では有限マクローリン展開を用いた近似値や近似誤差の計算結果の直感的な理解を行うにあたって近似値と近似誤差の可視化を行いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$3$章「微分($1$変数)」を主に参考にしました。
・数学まとめ
https://www.hello-statisticians.com/math_basic
有限マクローリン展開の式
$n$次の有限マクローリン展開は下記のような式で表される。
$$
\large
\begin{align}
f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!}x^k + \frac{f^{(n)}(\theta x)}{n!} x^{n}, \quad 0 \leq \theta \leq 1
\end{align}
$$
上記を元に近似値の計算を行う場合は、$n-1$次までの項を元に近似値を計算し、$n$次の項を元に誤差に関して考察を行えばよい。また、$n$次の有限テイラー展開は下記で取りまとめを行なった。
近似誤差の可視化
指数関数のマクローリン展開による近似
$$
\large
\begin{align}
e^{\frac{x}{2}} = 1 + \frac{1}{2}x + \frac{1}{8}x^2 + \frac{1}{48}x^3 + \frac{e^{\frac{\theta x}{2}}}{384} x^{4}
\end{align}
$$
以下、上記の例の可視化を行う。下記を実行することで$\displaystyle e^{\frac{x}{2}}$のマクローリン展開による近似の図示を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2., 3.01, 0.01)
y = np.e**(x/2.)
y_maclaurin = 1. + x/2. + x**2/8. + x**3/48.
epsilon = np.e**(x/2.)*(x**4)/384.
plt.plot(x,y,label="y")
plt.plot(x,y_maclaurin,label="y_maclaurin")
plt.fill_between(x, y_maclaurin-epsilon, y_maclaurin+epsilon, alpha=0.3)
plt.xlim([-2.1,3.1])
plt.legend()
plt.show()・実行結果
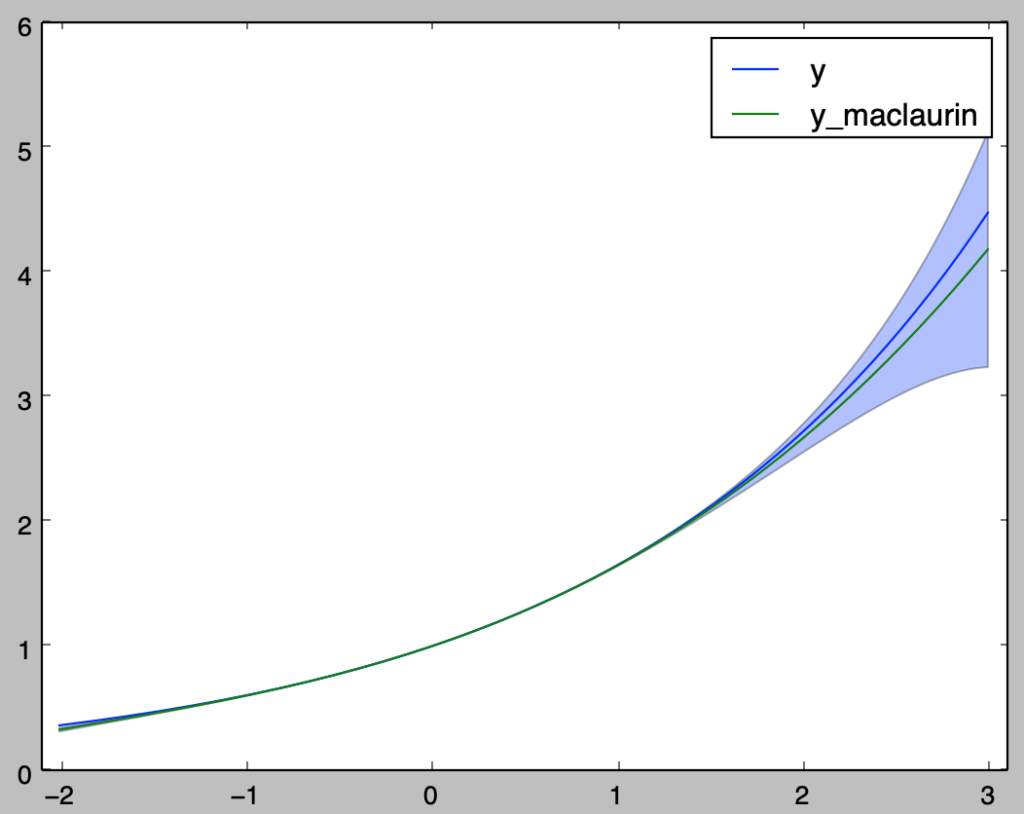

[…] ・有限マクローリン展開を用いた近似値・近似誤差の計算 […]