階段形(echelon form)の判定法と主番号・主列・主成分の定義の確認

行列の階段形(echelon form)や簡約階段形(reduced echelon form)は交代行列の対角化を考える際などに出てくる考え方であり抑えておくと良いです。当記事では階段形の判定法と主番号・主列・主成分の定義の確認に関して取りまとめを行いました。
作成にあたっては「チャート式シリーズ 大学教養 線形代数」の第$2.2$節「行列の行基本変形」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

階段形の概要

階段形の定義

「$m \times n$行列$A = (a_{ij})$が階段形である」 $\iff$ 「$0 \leq r \leq m, \, r,m \in \mathbb{R}$のように定める整数$r$に関して$1 \leq c_1 < c_2 < \cdots < c_r \leq n$が存在し以下の$[1]$〜$[3]$が成立する」のように定める。

$[1] \quad$ $1 \leq i \leq r$および$1 \leq j \leq c_i-1$のとき$a_{ij}=0$
$[2] \quad$ $r+1 \leq i \leq m$のとき$1 \leq j \leq n$の全ての$j$に関して$a_{ij}=0$
$[3] \quad$ $1 \leq i \leq r$のとき$a_{ic_i} \neq 0$

上記の定義だけではわかりにくいので下記の行列を元に階段形の確認を行う。
$$
\large
\begin{align}
\left( \begin{array}{ccccccc} a_{1c_1} & a_{1c_2} & \cdots & a_{1c_r} & a_{1,c_r+1} & \cdots & a_{1n} \\ a_{2c_1} & a_{2c_2} & \cdots & a_{2c_r} & a_{2,c_r+1} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{rc_1} & a_{rc_2} & \cdots & a_{rc_r} & a_{r,c_r+1} & \cdots & a_{rn} \\ a_{r+1,c_1} & a_{r+1,c_2} & \cdots & a_{r+1,c_r} & a_{r+1,c_r+1} & \cdots & a_{r+1,n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{mc_1} & a_{mc_2} & \cdots & a_{mc_r} & a_{m,c_r+1} & \cdots & a_{mn} \end{array} \right)
\end{align}
$$

上記に対して$[1]$〜$[3]$を適用すると下記のように行列を表せる。

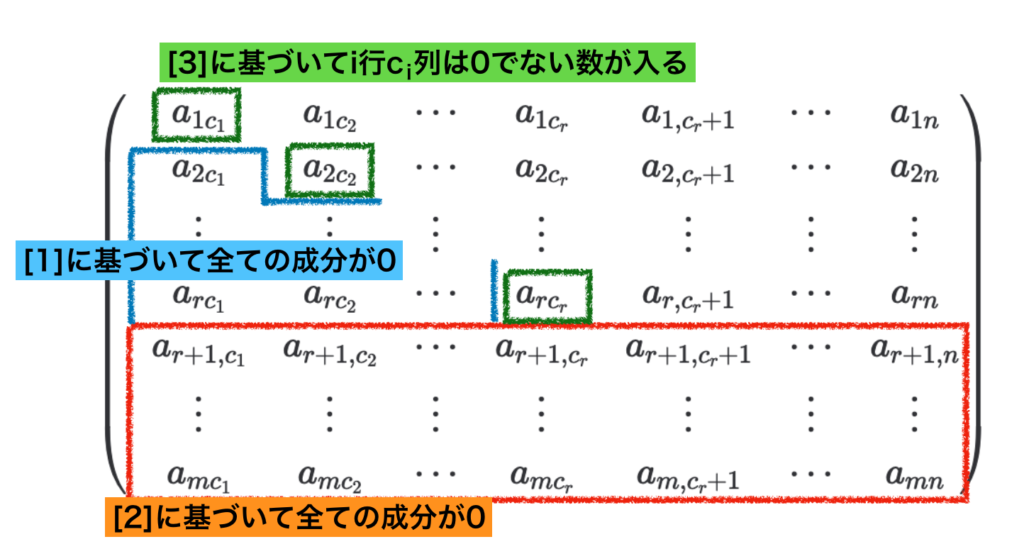
図を元に$1 \leq c_1 < c_2 < \cdots < c_r \leq n$に関して改めて確認しておくと良い。

主番号・主列・主成分の定義

階段形で表される行列の$i = 1, 2, \cdots, r$に対して$c_i = c_1, c_2, \cdots, c_r$を主番号、$(i,c_i)$成分を$i$番目の主成分という。また、$c_i$番目の列を$i$番目の主列ベクトルという。それぞれ下図と対応させて抑えておくと良い。

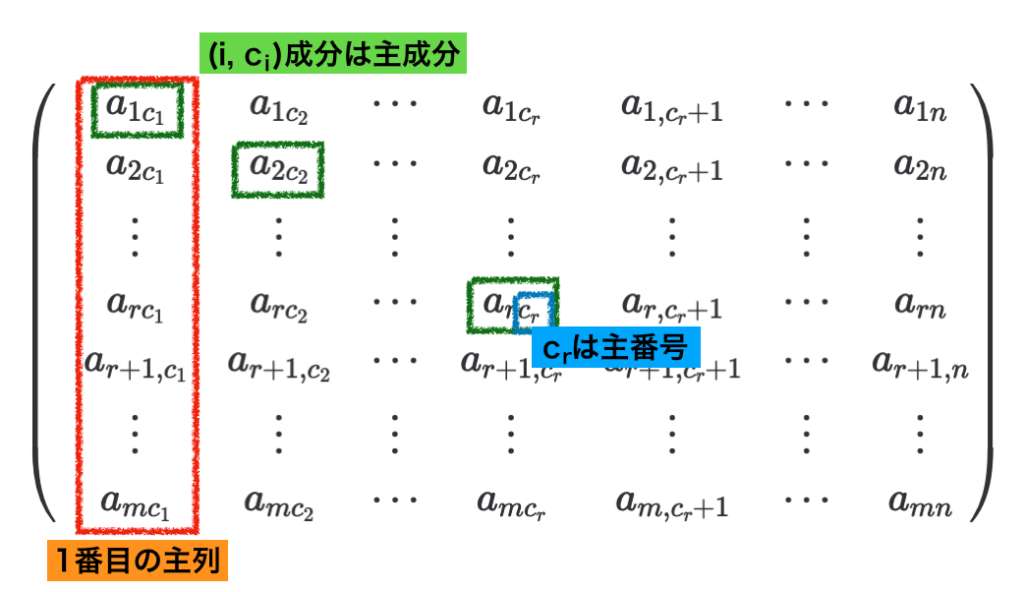
階段形に関する定義の確認

以下、「チャート式シリーズ 大学教養 線形代数」の例題の確認を行う。

基本例題$025$

$$
\large
\begin{align}
\left( \begin{array}{cccc} 0 & 1 & 2 & 3 \\ 0 & 4 & 5 & 0 \\ 6 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align}
$$

上記は$(2,2)$成分や$(3,1)$成分が$0$でないことから階段形ではない。

$$
\large
\begin{align}
\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 0 \\ 0 & 0 & 6 \end{array} \right)
\end{align}
$$

上記は$(2,1)$成分が$0$でないことから階段形ではない。

$$
\large
\begin{align}
\left( \begin{array}{cccc} 0 & 1 & 2 & 4 \\ 0 & 0 & 8 & 4 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align}
$$

上記は階段形の行列であり、主番号は$2$と$3$である。以下、それぞれの主番号に関して主列と主成分の確認を行う。

・主番号$2$
主列は$\displaystyle \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right)$、主成分は$1$

・主番号$3$
主列は$\displaystyle \left( \begin{array}{c} 2 \\ 8 \\ 0 \end{array} \right)$、主成分は$8$

基本例題$026$