ロルの定理を用いたテイラーの定理の証明と有限テイラー展開の近似誤差

テイラーの定理は有限テイラー展開や級数の形式のテイラー展開を考える上で用いられる重要な定理です。当記事ではテイラーの定理の理解にあたって、平均値の定理の特殊な場合であるロルの定理を用いた証明や有限テイラー展開の近似誤差について具体的な例を元に確認を行いました。

「数研出版」の「大学教養 微分積分」の第$3.4$節「テイラーの定理」の内容を参考に作成を行いました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

テイラーの定理の証明

ロルの定理

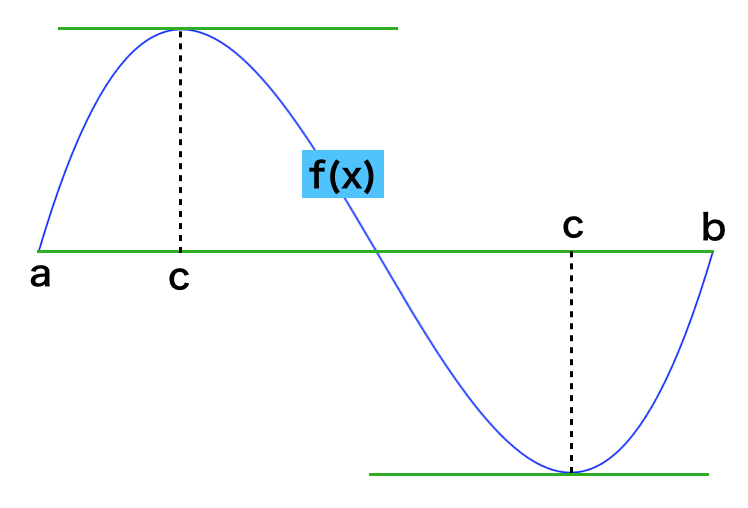
ロルの定理は上図を元に理解するとわかりやすい。閉区間$a \leq x \leq b$で連続関数$f(x)$を考えるとき、$f(x)$が開区間$a < x < b$で微分可能かつ$f(a)=f(b)$を仮定する。

このとき「$f'(c)=0$となる$c \in (a,b)$が少なくとも$1$つ存在する」と考えるのがロルの定理である。ロルの定理を数式を元に表すとやや抽象的だが、図で表したように「$f(a)$と$f(b)$が同じであれば途中のどこかの点で$f(x)$の傾きが$0$になる」と直感的に考えれば十分である。

ロルの定理の証明は「大学教養 微分積分」の第$3.2$節「微分法の応用」で取り扱われているので詳しくは参照すると良い。

平均値の定理

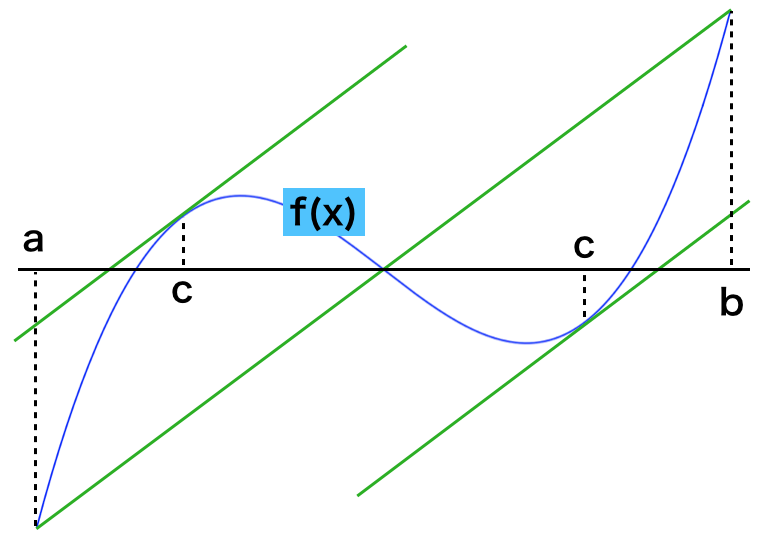
上図のように閉区間$a \leq x \leq b$で連続関数$f(x)$を考えるとき、$f(x)$が開区間$a < x < b$で微分可能を仮定する。このとき「$\displaystyle f'(c) = \frac{f(b)-f(a)}{b-a}$となる$c \in (a,b)$が少なくとも$1$つ存在する」と考えるのが平均値の定理である。

平均値の定理を数式を元に表すとロルの定理と同様にやや抽象的だが、図で表したように「$a$から$b$への傾きと途中のどこかの点の$f(x)$の傾きが一致する」と直感的に考えれば十分である。

平均値の定理の証明は「大学教養 微分積分」の第$3.2$節「微分法の応用」で取り扱われているので詳しくは参照すると良い。

テイラーの定理の証明

$$
\large
\begin{align}
f(x) = f(a) & + f'(a)(x-a)^{1} + \frac{1}{2}f^{”}(a)(x-a)^{2} + \cdots \\
& \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(x-a)^{n-1} + \frac{1}{n!}f^{(n)}(c_x)(x-a)^{n} \quad (1)
\end{align}
$$

「定義域$I$で$n$回微分可能な関数の$f(x)$は$I$上の全ての$x$に関して$a \in I$を考えるとき、上記の$(1)$式が成立する$a$と$x$の間の点の$c_x$が存在する」と考えるのがテイラーの定理である。以下、このテイラーの定理の証明を行う。

i) $x = a$のとき
$(1)$式に$x=a$を代入すると、下記のように表せる。
$$
\large
\begin{align}
f(x) &= f(a) + f'(a)(x-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(x-a)^{n-1} + \frac{1}{n!}f^{(n)}(c_x)(x-a)^{n} \quad (1) \\
f(a) &= f(a) + f'(a)(a-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(a-a)^{n-1} + \frac{1}{n!}f^{(n)}(c_x)(a-a)^{n} \\
&= f(a)
\end{align}
$$

よって$x=a$のとき$c_x$の値によらず$(1)$式が成立するので、$c_x=a \in I$で$(1)$式が成立する。

ⅱ) $x \neq a$のとき
$b \neq a$である任意の$b \in I$に関して下記が成立することを示せば良い。
$$
\large
\begin{align}
f(b) &= f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} + \frac{1}{n!}f^{(n)}(c_b)(b-a)^{n} \quad (1)’
\end{align}
$$

ここで下記が成立するように定数$A$を定める。
$$
\large
\begin{align}
A(b-a)^{n} = f(b) – \left[ f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} \right]
\end{align}
$$

また、下記のように$I$上の関数$g(x)$を定義する。
$$
\large
\begin{align}
g(x) &= f(b) – \left[ f(x) + f'(x)(b-x)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(x)(b-x)^{n-1} \right] – A(b-x)^{n} \\
&= f(b) – \left[ f(x) + f'(x)(b-x)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(x)(b-x)^{n-1} + A(b-x)^{n} \right]
\end{align}
$$

このとき$g(a), g(b)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
g(a) &= f(b) – \left[ f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} + A(b-a)^{n} \right] \\
&= \left[ f(b) – f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} \right] – A(b-a)^{n} \\
&= A(b-a)^{n} – A(b-a)^{n} = 0 \\
g(b) &= f(b) – \left[ f(b) + f'(x)(b-b)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(b)(b-b)^{n-1} + A(b-b)^{n} \right] \\
&= f(b) – f(b) = 0
\end{align}
$$

よって$g(a)=g(b)=0$が成り立つのでロルの定理より、$g'(c_b)=0$となる$c_b$が$a$と$b$の間に存在する。

次に$g'(x)$の計算を行う。$k \geq 1$のとき下記が成立する。
$$
\large
\begin{align}
\left( \frac{1}{k!} f^{(k)}(x)(b-x)^{k} \right)’ &= \frac{1}{k!} f^{(k+1)}(x)(b-x)^{k} + \frac{k}{k!} f^{(k+1)}(x)(b-x)^{k-1} \times (b-x)’ \\
&= \frac{1}{k!} f^{(k+1)}(x)(b-x)^{k} – \frac{k}{k!} f^{(k+1)}(x)(b-x)^{k-1}
\end{align}
$$

よって$g'(x)$は下記のように計算できる。
$$
\large
\begin{align}
g'(x) &= \\
&= -\frac{1}{(n-1)!} f^{(n)}(x) (b-x)^{n-1} + nA(b-x)^{n-1}
\end{align}
$$

ここで$g'(c_b)=0$であるから下記が成立する。
$$
\large
\begin{align}
g'(c_b) &= -\frac{1}{(n-1)!} f^{(n)}(c_b) (b-c_b)^{n-1} + nA(b-c_b)^{n-1} = 0 \\
nA \cancel{(b-c_b)^{n-1}} &= \frac{1}{(n-1)!} f^{(n)}(c_b) \cancel{(b-c_b)^{n-1}} \\
A &= \frac{1}{n!} f^{(n)}(c_b)
\end{align}
$$

$g(a)=0$の式に$\displaystyle A = \frac{1}{n!} f^{(n)}(c_b)$を代入すると下記が得られる。
$$
\large
\begin{align}
g(a) = f(b) – \left[ f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} + A(b-a)^{n} \right] &= 0 \\
f(b) – \left[ f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} + \frac{1}{n!} f^{(n)}(c_b)(b-a)^{n} \right] &= 0 \\
f(b) = f(a) + f'(a)(b-a)^{1} + \cdots + \frac{1}{(n-1)!}f^{(n-1)}(a)(b-a)^{n-1} + \frac{1}{n!}f^{(n)}(c_b)(b-a)^{n} & \quad (1)’
\end{align}
$$

上記のように$(1)’$式が得られるので、$(1)’$式が成立する。

したがって$(1)$式で表されたテイラーの定理は$x \in I$の全ての$x$で成立する。

有限テイラー展開の近似精度

有限テイラー展開の数式

有限テイラー展開の近似精度

参考

・有限マクローリン展開を用いた近似値・近似誤差の計算