指数関数・対数関数は統計学でよく用いられる関数であり、確率分布を考える際の正規分布などの指数型分布族や、最尤推定を行う際に対数尤度を計算するなどでも用いられます。当記事では指数関数・対数関数の式変形がスムーズに行えるように、基本的な定義や公式に関して演習の作成を行いました。
・統計学 基本演習$100$選
https://www.hello-statisticians.com/practice_100_basic
演習は主に下記の内容などに基づいて作成を行いましたので、以下を合わせて確認すると良いと思います。
Contents
基本問題
指数関数・対数関数の定義と公式
・問題
・解答
・解説
指数関数・対数関数のグラフ
・問題
・解答
・解説
ネイピア数$e$の定義と関連の式の導出
・問題
$$
\large
\begin{align}
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^{n} = e \quad (1)
\end{align}
$$
ネイピア数$e$は上記の$(1)$式で定義される数であり、数字で表すと$e=2.71…$である。指数関数・対数関数に関する微分などの演算は上記のように定めた$e$を用いるとシンプルに表すことができるので、$e$の定義の式は重要である。
一方で微分の公式の導出などの計算はなかなか複雑であるので、$e$の定義に関しては演習を繰り返すことで抑えておくと良い。よってこの問題では以下、$e$の定義や関連する式の導出に関して取り扱いを行う。ここまでの内容を元に下記の問題に答えよ。
i) $\displaystyle \left( 1 + \frac{1}{n} \right)^{n}$に$n=1,2,3$をそれぞれ代入し、値の計算を行え。
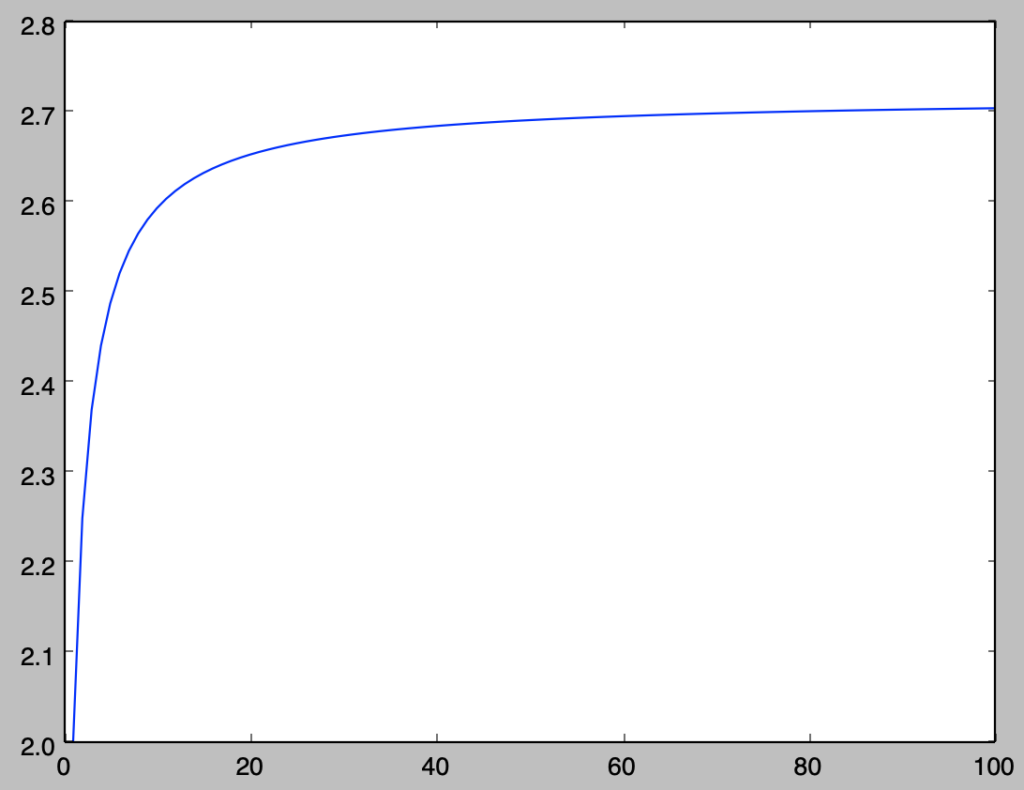
ⅱ) プログラムなどを用いることで$n=1$〜$n=100$までの$\displaystyle \left( 1 + \frac{1}{n} \right)^{n}$の値を計算し、グラフの描画を行え。
ⅲ) 下記の式が成立することを示せ。
$$
\begin{align}
\left( 1 – \frac{1}{t} \right)^{-t} = \left( 1 + \frac{1}{t-1} \right)^{t-1} \times \left( 1 + \frac{1}{t-1} \right)
\end{align}
$$
iv) 下記の式に対し、$t=-n$とおき、ⅲ)の変形を用いることで下記の式を示せ。
$$
\begin{align}
\lim_{n \to -\infty} \left( 1 + \frac{1}{n} \right)^{n} = e
\end{align}
$$
v) $\displaystyle n=\frac{1}{h}$を考えることで下記の式を示せ。
$$
\large
\begin{align}
\lim_{h \to 0} \left( 1 + h \right)^{\frac{1}{h}} = e
\end{align}
$$
・解答
i)
$\displaystyle \left( 1 + \frac{1}{1} \right)^{1}, \left( 1 + \frac{1}{2} \right)^{2}, \left( 1 + \frac{1}{3} \right)^{3}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\left( 1 + \frac{1}{1} \right)^{1} &= (1+1)^{1} =2 \\
\left( 1 + \frac{1}{2} \right)^{2} &= \left( \frac{3}{2} \right)^{2} \\
&= \frac{9}{4} = 2.25 \\
\left( 1 + \frac{1}{3} \right)^{3} &= \left( \frac{4}{3} \right)^{3} \\
&= \frac{64}{27} = 2.370370…
\end{align}
$$
ⅱ)
下記を実行することで$n=1$〜$n=100$までの$\displaystyle \left( 1 + \frac{1}{n} \right)^{n}$の値を計算し、グラフの描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
n = np.arange(1.,101.,1.)
y_n = np.zeros([100])
for i in range(100):
y_n[i] = (1.+1./n[i])**n[i]
plt.plot(n,y_n)
plt.show()実行結果
ⅲ)
$\displaystyle \left( 1 – \frac{1}{t} \right)^{-t}$は下記のように式変形できる。
$$
\large
\begin{align}
\left( 1 – \frac{1}{t} \right)^{-t} &= \left( \frac{t-1}{t} \right)^{-t} \\
&= \left( \frac{t}{t-1} \right)^{t} \\
&= \left( \frac{(t-1)+1}{t-1} \right)^{t} \\
&= \left( 1 + \frac{1}{t-1} \right)^{t} \\
&= \left( 1 + \frac{1}{t-1} \right)^{t-1} \times \left( 1 + \frac{1}{t-1} \right)
\end{align}
$$
iv)
$t=-n$とおくことで、下記のように示すことができる。
$$
\large
\begin{align}
\lim_{n \to -\infty} \left( 1 + \frac{1}{n} \right)^{n} &= \lim_{t \to \infty} \left( 1 + \frac{1}{-t} \right)^{-t} \\
&= \lim_{t \to \infty} \left( 1 – \frac{1}{t} \right)^{-t} \\
&= \lim_{t \to \infty, t-1 \to \infty} \left[ \left( 1 + \frac{1}{t-1} \right)^{t-1} \times \left( 1 + \frac{1}{t-1} \right) \right] \\
&= e \times 1 \\
&= e
\end{align}
$$
v)
$h>0$のとき、$\displaystyle n=\frac{1}{h}$とおくことで、下記のように示すことができる。
$$
\large
\begin{align}
\lim_{h \to +0} \left( 1 + h \right)^{\frac{1}{h}} &= \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^{n} \\
&= e
\end{align}
$$
$h<0$のときも同様に$\displaystyle n=\frac{1}{h}$とおくことで、下記のように示すことができる。
$$
\large
\begin{align}
\lim_{h \to -0} \left( 1 + h \right)^{\frac{1}{h}} &= \lim_{n \to -\infty} \left( 1 + \frac{1}{n} \right)^{n} \\
&= e
\end{align}
$$
・解説
v)の導出にあたっては$h \to +0$が$n \to \infty$に対応し、$h \to -0$が$n \to -\infty$に対応することは注意しておくと良いです。$n \to -\infty$の場合の式に関してはⅲ)、iv)で取り扱いましたが、式変形が少々複雑なので流れを抑えておくと良いと思います。
この問題で取り扱った$e$の定義は二項分布の確率関数の極限からポアソン分布の確率関数を導出する際に出てくるなど、統計学でもよく出てくるので重要なトピックであるので、繰り返して習得しておくと良いと思います。
発展問題
指数関数の微分の公式の導出
$$
\large
\begin{align}
f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \quad (1)
\end{align}
$$
関数$f(x)$の導関数$f'(x)$は$(1)$式のように定義される。指数関数$f(x)=e^{x}$を考える際に$f'(x)=e^{x}$のような公式があるが、公式は$(1)$式に基づいて導出されたものであるということは把握しておく必要がある。
この問題では以下、$(1)$式に基づいて指数関数$f(x)=e^{x}$の微分に関して$f'(x)=e^{x}$が成立することを示し、式変形を行うことで$a^{x}, \, a>0$の微分の公式について同時に示す。ここまでの内容を元に下記の問題に答えよ。
i) $f(x)=e^{x}$ に関して$(1)$式を適用し、$f'(x)$が下記のように表せることを確認せよ。
$$
\begin{align}
f'(x) = \lim_{h \to 0} e^{x} \cdot \frac{e^{h}-1}{h}
\end{align}
$$
ⅱ) $\displaystyle \lim_{h \to 0} \frac{e^{h}-1}{h}=1$を$k=e^{h}-1$とおくことで示せ。
ⅲ) $(e^{x})’=e^{x}$を示せ。
iv) $a^{x}=e^{\log_{e}{a} x}$が成立することを確認せよ。
v) iv)の結果と合成関数の微分の公式を用いて$(a^{x})’=a^{x}\log_{e}{a}$が成立することを示せ。
・解答
i)
$f(x)=e^{x}$ に関して$(1)$式を適用することで、$f'(x)$は下記のように表せる。
$$
\large
\begin{align}
f'(x) &= \lim_{h \to 0} \frac{e^{x+h}-e^{x}}{h} \\
&= \lim_{h \to 0} \frac{e^{x}e^{h}-e^{x}}{h} \\
&= \lim_{h \to 0} e^{x} \cdot \frac{e^{h}-1}{h}
\end{align}
$$
ⅱ)
$k=e^{h}-1$は$h$に関して下記のように解ける。
$$
\large
\begin{align}
k &= e^{h}-1 \\
e^{h} &= k+1 \\
h &= \log_{e}{(k+1)}
\end{align}
$$
また、$h \to 0$のとき$k \to 0$である。よって、$\displaystyle \lim_{h \to 0} \frac{e^{h}-1}{h}$は下記のように考えることができる。
$$
\large
\begin{align}
\lim_{h \to 0} \frac{e^{h}-1}{h} &= \lim_{k \to 0} \frac{k}{\log_{e}{(k+1)}} \\
&= \lim_{k \to 0} \frac{1}{\displaystyle \frac{1}{k} \log_{e}{(k+1)}} \\
&= \lim_{k \to 0} \frac{1}{\log_{e}{(1+k)^{\frac{1}{k}}}} \\
&= \frac{1}{\log_{e}{e}} \\
&= \frac{1}{1} = 1
\end{align}
$$
ⅲ)
i)、ⅱ)の結果を元に$(e^{x})’=e^{x}$は下記のように示すことができる。
$$
\large
\begin{align}
(e^{x})’ &= \lim_{h \to 0} \frac{e^{x+h}-e^{x}}{h} \\
&= \lim_{h \to 0} e^{x} \cdot \frac{e^{h}-1}{h} \\
&= e^{x} \cdot 1 = e^{x}
\end{align}
$$
iv)
対数の定義より、$e$の$\log_{e}{a}$乗は$a$である。よって$a=e^{\log_{e}{a}}$が成立するので、同時に$a^{x}=e^{\log_{e}{a} x}$も成立する。
v)
$(a^{x})’$は下記のように計算できる。
$$
\large
\begin{align}
(a^{x})’ &= (e^{\log_{e}{a} x}) \\
&= \log_{e}{a} e^{\log_{e}{a} x} \\
&= a^{x} \log_{e}{a}
\end{align}
$$
・解説
指数関数の微分を考えるにあたっては$(e^{x})’=e^{x}$に基づいて$(a^{x})’=a^{x} \log_{e}{a}$は導出できるので、$(e^{x})’=e^{x}$の導出の流れは一通り確認しておくと良いと思います。
対数関数の微分の公式の導出
・問題
$$
\large
\begin{align}
f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \quad (1)
\end{align}
$$
関数$f(x)$の導関数$f'(x)$は$(1)$式のように定義される。対数関数$f(x)=\log_{e}{x}$を考える際に$\displaystyle f'(x) = \frac{1}{x}$のような公式があるが、公式は$(1)$式に基づいて導出されたものであるということは把握しておく必要がある。
この問題では以下、$(1)$式に基づいて$\displaystyle (\log_{e}{x})’ = \frac{1}{x}$が成立することを示し、式変形を行うことで$\log_{a}{x}, \, a>0, a \neq 0$の微分の公式について同時に示す。ここまでの内容を元に下記の問題に答えよ。
i) $f(x)=\log_{e}{x}$ に関して$(1)$式を適用し、$f'(x)$が下記のように表せることを確認せよ。
$$
\begin{align}
f'(x) = \lim_{h \to 0} \log_{e}{\left( 1 + \frac{h}{x} \right)}^{\frac{1}{h}}
\end{align}
$$
ⅱ) $(2^3)^2, 2^6$をそれぞれ計算し、結果が一致することを確かめよ。
ⅲ) ⅱ)で確認したように$(a^{x})^{y}=a^{xy}$が成立することとネイピア数の定義に基づいて、$(1)$式を元に$\displaystyle (\log_{e}{x})’ = \frac{1}{x}$を導出せよ。
iv) 底の変換公式を用いて$\log_{a}{x}, \, a>0, a \neq 0$を$e$を底とする対数関数に変換せよ。
v) iv)の結果と合成関数の微分の公式を用いて$\displaystyle (\log_{a}{x})’=\frac{1}{x \log_{e}{a}}$が成立することを示せ。
・解答
i)
$f(x)=\log_{e}{x}$ に関して$(1)$式を適用することで、$f'(x)$は下記のように表せる。
$$
\large
\begin{align}
f'(x) &= \lim_{h \to 0} \frac{\log_{e}{(x+h)}-\log_{e}{x}}{h} \\
&= \lim_{h \to 0} \frac{1}{h} \log_{e}{\frac{x+h}{x}} \\
&= \lim_{h \to 0} \log_{e}{\left( 1 + \frac{h}{x} \right)}^{\frac{1}{h}}
\end{align}
$$
ⅱ)
$(2^3)^2=8^2=64, 2^6=64$より、$(2^3)^2=2^6$が成立することが確認できる。
ⅲ)
$\displaystyle (\log_{e}{x})’ = \frac{1}{x}$は下記のように示すことができる。
$$
\large
\begin{align}
(\log_{e}{x})’ &= \lim_{h \to 0} \frac{\log_{e}{(x+h)}-\log_{e}{x}}{h} \\
&= \lim_{h \to 0} \log_{e}{\left( 1 + \frac{h}{x} \right)}^{\frac{1}{h}} \\
&= \lim_{h \to 0} \log_{e}{\left[ \left( 1 + \frac{h}{x} \right)^{\frac{x}{h}} \right]^{\frac{1}{x}}} \\
&= \lim_{h \to 0} \frac{1}{x} \log_{e}{\left( 1 + \frac{h}{x} \right)^{\frac{x}{h}}} \\
&= \frac{1}{x} \log_{e}{e} = \frac{1}{x}
\end{align}
$$
iv)
底の変換公式を用いることで$\log_{a}{x}, \, a>0, a \neq 0$は下記のように変形できる。
$$
\large
\begin{align}
\log_{a}{x} &= \frac{\log_{e}{x}}{\log_{e}{a}}
\end{align}
$$
v)
$\displaystyle (\log_{a}{x})’$は下記のように計算できる。
$$
\large
\begin{align}
(\log_{a}{x})’ &= \left( \frac{\log_{e}{x}}{\log_{e}{a}} \right)’ \\
&= \frac{1}{x \log_{e}{a}}
\end{align}
$$
・解説
対数関数の微分を考えるにあたっては$\displaystyle (\log_{e}{x})’ = \frac{1}{x}$に基づいて$\displaystyle (\log_{a}{x})’=\frac{1}{x \log_{e}{a}}$は導出できるので、$(\log_{e}{x})’$の導出の流れは一通り確認しておくと良いと思います。
