当記事では「統計学を学ぶにあたって最低限抑えておきたい数学」の中から「指数関数・対数関数とその応用」に関して取り扱います。指数関数は正規分布や指数分布などの確率分布で用いられることが多く、対数関数は最尤法で対数尤度を考える際によく用いられます。
取りまとめにあたっては数学の解説に関してはなるべくシンプルに取り扱いますが、統計学への応用に関連した複雑な内容に関しては目次に「*」をつけました。「*」がついているものはやや難しいので、読み飛ばしても問題ありません。
・基本数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
指数関数
指数関数の概要
$f(x) = a^{x},a>0$で表される関数を指数関数といいます。指数関数を理解するにあたっては$1$次関数や$2$次関数と同様にグラフの描画を行うとわかりやすいです。以下、Pythonを用いてグラフの描画を行います。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2,2.01,0.01)
x_ = np.arange(-2,3,1)
a = np.array([2,0.5,1.5,1.])
for i in range(a.shape[0]):
y, y_ = a[i]**x, a[i]**x_
plt.subplot(2,2,i+1)
plt.ylim([-1,5])
plt.title("f(x) = {}^x".format(a[i]))
plt.plot(x,y)
plt.scatter(x_,y_)
plt.show()・実行結果
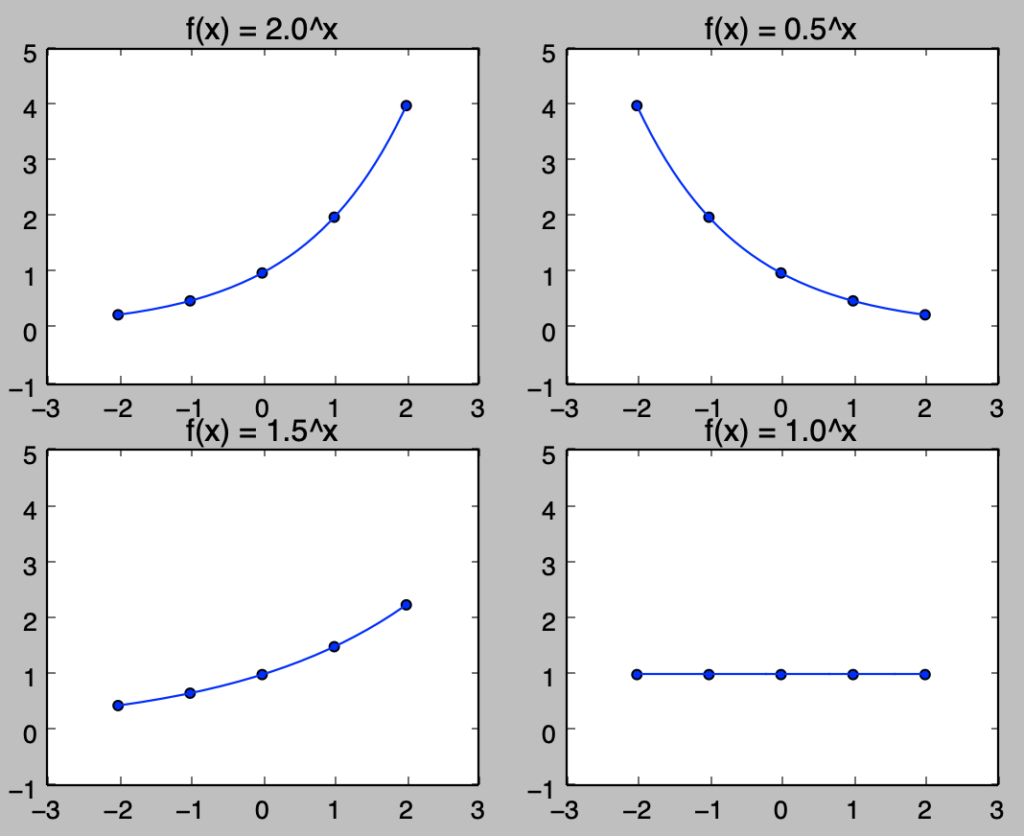
上図より、$a>1$のとき単調増加、$0<a<1$のとき単調減少、$a=1$のとき$f(x)=1$の定数関数であることがそれぞれ確認できます。
指数関数に関する基本公式
$a>0$の指数関数$a^x, a^y$に関して下記が成立する。
$$
\large
\begin{align}
a^{x} \times a^{y} &= a^{x+y} \\
(a^{x})^{n} &= a^{nx}
\end{align}
$$
底の変換公式
$$
\large
\begin{align}
\log_{a}{b} &= \frac{\log_{c}{b}}{\log_{c}{a}} \\
\log_{a}{x} &= \frac{1}{\log_{x}{a}}
\end{align}
$$
指数関数とネイピア数$e$*
$$
\large
\begin{align}
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^{n} = e = 2.71…
\end{align}
$$
上記のように定義されるネイピア数$e$を用いることで指数関数や対数関数の微分などを行う際に有用です。極限や指数関数や対数関数の微分は数Ⅲのトピックでありやや難しいのでここでは省略しますが、下記で詳しくまとめましたので余裕のある際に確認してみると良いかもしれません。
・参考
ネイピア数$e$の定義と指数関数・対数関数の微分の導出
https://www.hello-statisticians.com/explain-terms-cat/def_napier1.html
対数関数
対数関数の概要
対数関数は$0<a<1$or$1<a$のとき$f(x)=\log_{a}(x),x>0$のように表します。対数関数は指数関数の逆関数であり、$y=\log_{a}(x)$は$a^{y}=x$が対応します。要するに「$a$を$\log_{a}(x)$乗すれば$x$になる」と考えれば良いです。
これまで取り扱った関数と同様にグラフで確認するとわかりやすいので、以下、Pythonを用いてグラフの描画を行います。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.5,10.1,0.1)
x_ = np.arange(1,11,1)
a = [2,"e",10]
y = [np.log2(x), np.log(x), np.log10(x)]
y_ = [np.log2(x_), np.log(x_), np.log10(x_)]
for i in range(3):
plt.subplot(2,2,i+1)
plt.title("log_{}(x)".format(a[i]))
plt.plot(x,y[i])
plt.scatter(x_,y_[i])
plt.show()・実行結果
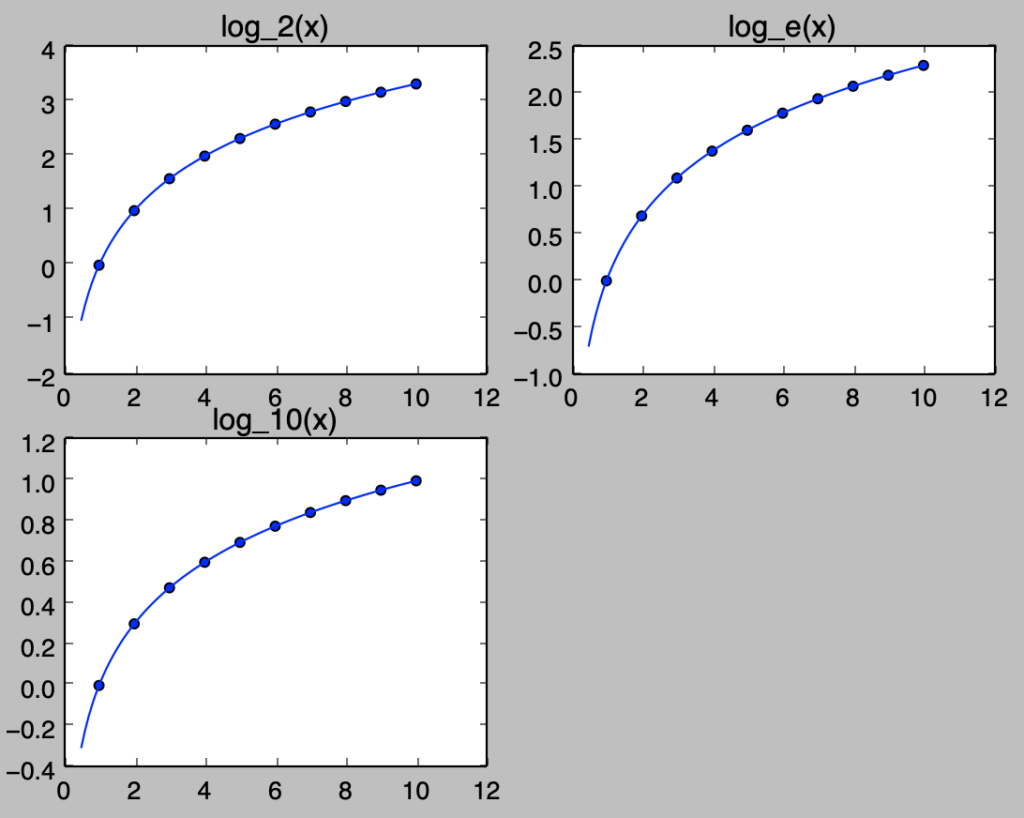
上記より$\log_{2}(2)=1, \log_{2}(4)=2, \log_{2}(8)=3, \log_{10}(1)=0, \log_{10}(10)=1$がそれぞれ確認できます。
対数に関する公式
対数$\log_{a}(x)$に関して、下記の公式が成立することは抑えておくと良いです。
$$
\large
\begin{align}
\log_{a}(AB) &= \log_{a}{A} + \log_{a}{B} \\
\log_{a}(A^{n}) &= n \log_{a}{A}
\end{align}
$$
指数関数と対数関数の応用
指数関数と確率分布
「確率分布」を大まかに理解するにあたっては「ヒストグラムの確率化を行なったもの」と考えると良いです。この確率分布を考える上で指数関数はよく用いられます。以下、代表例の指数分布と正規分布をご紹介します。

[…] […]