多次元正規分布と二次形式(Mahalanobis distance)の直感的な理解

多次元正規分布(Multidimensional normal distribution)の式を理解するにあたっては二次形式の理解が重要となる。当記事では「パターン認識と機械学習」の$2.3$節の記載を参考に、多次元正規分布を二次形式の視点から確認するものとする。

前提の理解

直交行列の概要

$\mathbf{U}$を$n$行$n$列の行列、$\mathbf{I}$を$n$行$n$列の単位行列とする。この際に、以下が成立する$\mathbf{U}$は直交行列と呼ばれる。
$$
\large
\begin{align}
\mathbf{U}\mathbf{U}^{\mathrm{T}} = \mathbf{U}^{\mathrm{T}}\mathbf{U} = \mathbf{I}
\end{align}
$$

上記は逆行列の定義式$\mathbf{U}\mathbf{U}^{-1} = \mathbf{U}^{-1}\mathbf{U} = \mathbf{I}$と同様の形式だが、逆行列の定義式は一般的な行列について成り立つ一方で、直交行列の式は必ずしも一般的な式では成立しない。また、二つの定義式を見比べることで、直交行列に関して下記が成立することもわかる。
$$
\large
\begin{align}
\mathbf{U}^{-1} = \mathbf{U}^{\mathrm{T}}
\end{align}
$$
直交行列は少々特殊な行列だが、固有ベクトルを元にした議論を行う際に利用するなど、重要なトピックである。

直交行列の理解

直交行列のような計算を行うことができる原理を理解するにあたっては、直交する長さが$1$の単位ベクトルを並べた行列を考えることで直交行列を作成することができることについて知っておくとよい。具体的に考える方がわかりやすいので、簡単な例を元に確認する。
$$
\large
\begin{align}
\mathbf{u}_1 &= \frac{1}{\sqrt{5}}\left(\begin{array}{c} 2 \\ 1 \end{array} \right) \\
\mathbf{u}_2 &= \frac{1}{\sqrt{5}}\left(\begin{array}{c} -1 \\ 2 \end{array} \right)
\end{align}
$$

上記のような$\mathbf{u}_1$、$\mathbf{u}_2$を考えた際に、$\mathbf{u}_1 \cdot \mathbf{u}_2 = 0$かつ$|\mathbf{u}_1| \neq 0$かつ$|\mathbf{u}_2| \neq 0$が成立するので、$\mathbf{u}_1$と$\mathbf{u}_2$は直交することがわかる。ここで$1$行目を$\mathbf{u}_1^{\mathrm{T}}$、$2$行目を$\mathbf{u}_2^{\mathrm{T}}$とする行列$\mathbf{U}$を考えると、$\mathbf{U}$は下記のように表すことができる。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle \frac{1}{\sqrt{5}} \\ \displaystyle -\frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right)
\end{align}
$$

このとき、$\det(\mathbf{U})$を求めると下記のようになる。
$$
\large
\begin{align}
\det(\mathbf{U}) &= \frac{2}{\sqrt{5}} \times \frac{2}{\sqrt{5}} – \left( -\frac{1}{\sqrt{5}} \right) \times \frac{1}{\sqrt{5}} \\
&= \frac{4}{5} + \frac{1}{5} \\
&= 1
\end{align}
$$

よって、$\mathbf{U}^{-1}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{U}^{-1} &= \frac{1}{\det(\mathbf{U})} \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle -\frac{1}{\sqrt{5}} \\ \displaystyle \frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right) \\
&= \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle -\frac{1}{\sqrt{5}} \\ \displaystyle \frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right)
\end{align}
$$

逆行列の公式を用いた計算に過ぎないためここでは詳細は省略するが、$\mathbf{U}\mathbf{U}^{\mathrm{T}}=\mathbf{I}$となることは行列の積を計算することで確認できる。

ここでは直交行列が主題なので、以下では逆行列と行列の転置が一致することについて詳しく確認を行う。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle \frac{1}{\sqrt{5}} \\ \displaystyle -\frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right) \\
\mathbf{U}^{-1} &= \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle -\frac{1}{\sqrt{5}} \\ \displaystyle \frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right) \\
\mathbf{U}^{\mathrm{T}} &= \left(\begin{array}{cc} \displaystyle \frac{2}{\sqrt{5}} & \displaystyle -\frac{1}{\sqrt{5}} \\ \displaystyle \frac{1}{\sqrt{5}} & \displaystyle \frac{2}{\sqrt{5}} \end{array} \right)
\end{align}
$$

上記では逆行列と行列の転置の成分が一致することについて注目しておくとよい。これは直交行列で一般的に成立する。また、ここで$\det(\mathbf{U})=1$であることも直交行列では一般に成立することも抑えておくとよい。

ここで確認を行った、「直交行列は直交するベクトルを並べた行列で、逆行列と転置が一致する」ということは多くの議論の前提となるため重要である。

対称行列の固有値・固有ベクトルと直交行列

直交行列を考えるにあたって、同時に出てくることが多いのが対称行列の固有値・固有ベクトルである。対称行列の相異なる固有値に対応する固有ベクトルは直交するため、大きさが$1$になるように調整を行うだけで前述の手順に基づいて直交行列を作成することができる。導出は下記で取り扱った。

対称行列(symmetric matrix)の固有値と固有ベクトルの性質とその導出

$D$次元空間における分散共分散行列の$D$個の固有ベクトルを考えると、$i$番目の大きさ$1$の固有ベクトル$\mathbf{u}_i$は下記のように表せる。
$$
\large
\begin{align}
\mathbf{u}_i = \left(\begin{array}{c} u_{i1} \\ \vdots \\ u_{iD} \end{array} \right)
\end{align}
$$
$$
\large
\mathbf{u}_i^{\mathrm{T}} \mathbf{u}_j =
\begin{cases}
1 \quad (i = j) \\
0 \quad (i \neq j)
\end{cases}
\qquad (1)
$$

前項と同様に$\mathbf{u}_i^{\mathrm{T}}$を$i$行目とする行列$\mathbf{U}$を考えると、$\mathbf{U}$の要素は下記のようになる。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{c} \mathbf{u}_1^{\mathrm{T}} \\ \vdots \\ \mathbf{u}_D^{\mathrm{T}} \end{array} \right) \\
&= \left(\begin{array}{ccc} u_{11} & \cdots & u_{1D} \\ \vdots & \ddots & \vdots \\ u_{D1} & \cdots & u_{DD} \end{array} \right)
\end{align}
$$
ベクトルと行列の成分の対応がわからなくなりやすいため、上記において、$\mathbf{u}_i^{\mathrm{T}} = \left(\begin{array}{r} u_{i1} & \cdots & u_{iD} \end{array} \right)$であることは注意して確認しておくとよい。

ここで$\mathbf{U}$が直交行列となるため、下記が成立する。
$$
\begin{align}
\mathbf{U}\mathbf{U}^{\mathrm{T}} &= \mathbf{U}^{\mathrm{T}}\mathbf{U} = \mathbf{I} \\
\left(\begin{array}{ccc} u_{11} & \cdots & u_{1D} \\ \vdots & \ddots & \vdots \\ u_{D1} & \cdots & u_{DD} \end{array} \right)\left(\begin{array}{ccc} u_{11} & \cdots & u_{D1} \\ \vdots & \ddots & \vdots \\ u_{1D} & \cdots & u_{DD} \end{array} \right) &= \left(\begin{array}{ccc} u_{11} & \cdots & u_{D1} \\ \vdots & \ddots & \vdots \\ u_{1D} & .. & u_{DD} \end{array} \right)\left(\begin{array}{ccc} u_{11} & \cdots & u_{1D} \\ \vdots & \ddots & \vdots \\ u_{D1} & \cdots & u_{DD} \end{array} \right) = \left(\begin{array}{ccc} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{array} \right)
\end{align}
$$

上記を確認する際に、$\mathbf{U}\mathbf{U}^{\mathrm{T}}=\mathbf{I}$は$(1)$式からそのまま導出できる一方で、$\mathbf{U}^{\mathrm{T}}\mathbf{U}=\mathbf{I}$は逆行列の性質より導出していることは注意しておくとよい。

基底の変換と行列

線形代数学において基底(basis)は、線形独立のベクトルからなる集合である。
https://ja.wikipedia.org/wiki/基底_(線型代数学)
抽象的に確認すると難しいので、簡単な例を元に確認する。
$$
\large
\begin{align}
\mathbf{e}_1 &= \left(\begin{array}{c} 1 \\ 0 \end{array} \right) \\
\mathbf{e}_2 &= \left(\begin{array}{c} 0 \\ 1 \end{array} \right)
\end{align}
$$

たとえば上記のように定義した$\mathbf{e}_1$、$\mathbf{e}_2$は線形独立であるが、以下詳しく確認する。
$$
\large
\begin{align}
a\mathbf{e}_1+b\mathbf{e}_2 = \left(\begin{array}{c} 0 \\ 0 \end{array} \right) = \vec{0}
\end{align}
$$

$\mathbf{e}_1$、$\mathbf{e}_2$の線形独立は、$a\mathbf{e}_1+b\mathbf{e}_2=\vec{0}$のとき、$a=b=0$となることが確認できれば良いが、ベクトルの成分を比較することで$a=b=0$が導出できる。よって、$\mathbf{e}_1$、$\mathbf{e}_2$は線形独立であり、基底とすることができる。

ここで、下記のような$\mathbf{a}_1$、$\mathbf{a}_2$を考える。
$$
\large
\begin{align}
\mathbf{a}_1 &= \left(\begin{array}{c} 2 \\ 1 \end{array} \right) \\
\mathbf{a}_2 &= \left(\begin{array}{c} 1 \\ 2 \end{array} \right)
\end{align}
$$

$s\mathbf{a}_1+t\mathbf{a}_2=\vec{0}$を考えるとき、$2s+t=0$、$s+2t=0$の連立方程式を解くと$s=t=0$となるので$\mathbf{a}_1$、$\mathbf{a}_2$も線形独立であり、これも基底であると考えることができる。

線形独立と基底について確認できたので、次に「行列を用いた基底の変換」について取り扱う。
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array} \right) &= x\mathbf{e}_1 + y\mathbf{e}_2 \\
&= X\mathbf{a}_1 + Y\mathbf{a}_2
\end{align}
$$

ここで、上記のように考えた際に、$\displaystyle \left(\begin{array}{c} x \\ y \end{array} \right)$の基底を変換することを考えるとする。
このとき$\mathbf{a}_1$、$\mathbf{a}_2$は$\mathbf{e}_1$、$\mathbf{e}_2$を用いて表すことができることから二つの基底の組に対して以下のように関係式を作成する。
$$
\large
\begin{align}
\mathbf{a}_1 &= \left(\begin{array}{c} 2 \\ 1 \end{array} \right) \\
&= 2\mathbf{e}_1 + \mathbf{e}_2 \\
\mathbf{a}_2 &= \left(\begin{array}{c} 1 \\ 2 \end{array} \right) \\
&= \mathbf{e}_1 + 2\mathbf{e}_2
\end{align}
$$

これを$X\mathbf{a}_1 + Y\mathbf{a}_2$に代入すると下記のようになる。
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array} \right) &= X\mathbf{a}_1 + Y\mathbf{a}_2 \\
&= X(2\mathbf{e}_1 + \mathbf{e}_2) + Y(\mathbf{e}_1 + 2\mathbf{e}_2) \\
&= (2X + Y)\mathbf{e}_1 + (X + 2Y)\mathbf{e}_2 \\
&= \left(\begin{array}{c} 2X + Y \\ X + 2Y \end{array} \right) \\
&= \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \left(\begin{array}{c} X \\ Y \end{array} \right)
\end{align}
$$

上記より、それぞれの基底に対応する$\displaystyle \left(\begin{array}{c} x \\ y \end{array} \right)$と$\displaystyle \left(\begin{array}{c} X \\ Y \end{array} \right)$の値は下記のように行列を用いた変換で表すことができる。
$$
\large
\begin{align}
\left(\begin{array}{c} x \\ y \end{array} \right) &= \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \left(\begin{array}{c} X \\ Y \end{array} \right) \\
\left(\begin{array}{c} X \\ Y \end{array} \right) &= \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right)^{-1} \left(\begin{array}{c} x \\ y \end{array} \right)
\end{align}
$$

固有ベクトルと基底の変換

前項における$\mathbf{e}_1$、$\mathbf{e}_2$は$x$軸、$y$軸をそのまま使うことと同様なので、基本的には$\mathbf{e}_1$、$\mathbf{e}_2$を基底に用いることが多い。この変換にあたって、前項の$\mathbf{a}_1$、$\mathbf{a}_2$のような変換を用いると、逆行列を計算する必要が生じ、$2$行$2$列の行列の逆行列のようにシンプルな公式のない$3$行$3$列以上の行列であまり望ましくはない。この解決にあたっては、直交行列を用いて基底の変換を行うことを考えれば逆行列と行列の転置が一致するため、導出をシンプルに行うことができる。

大きさが$1$かつそれぞれが直交する正規直交基底を用いて作成した行列を用いて基底の変換を行うことで、逆変換の際に逆行列ではなく行列の転置を用いて計算できるので導出が行いやすい。大きさを$1$にした固有ベクトルは基本的には正規直交基底となるため、処理がシンプルになる。
$$
\large
\begin{align}
\mathbf{U} &= \left(\begin{array}{c} \mathbf{u}_1^{\mathrm{T}} \\ \vdots \\ \mathbf{u}_D^{\mathrm{T}} \end{array} \right) \\
&= \left(\begin{array}{ccc} u_{11} & \cdots & u_{1D} \\ \vdots & \ddots & \vdots \\ u_{D1} & \cdots & u_{DD} \end{array} \right)
\end{align}
$$

上記のように定義した$\mathbf{U}$を用いて、$D$次元ベクトル$\mathbf{x}$を$\mathbf{y}$に変換すると考えると、変換は下記のように記載できる。
$$
\large
\begin{align}
\mathbf{x} &= \mathbf{U}^{\mathrm{T}}\mathbf{y} \\
\mathbf{y} &= (\mathbf{U}^{\mathrm{T}})^{-1}\mathbf{x} \\
&= (\mathbf{U}^{\mathrm{T}})^{\mathrm{T}}\mathbf{x} \\
&= \mathbf{U}\mathbf{x}
\end{align}
$$

多次元正規分布の直感的理解

多次元正規分布の数式

多次元正規分布の数式は下記のように表すことができる。
$$
\large
\begin{align}
N(\mathbf{x}|\mathbf{\mu}, \mathbf{\Sigma}) = \frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} \exp \left( -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu}) \right) \quad (2)
\end{align}
$$

上記の式における$\mathbf{\mu}$は平均ベクトル、$\mathbf{\Sigma}$は分散共分散行列をそれぞれ表す。

分散共分散行列の逆行列の導出

以下、多次元正規分布の式に現れる$\mathbf{\Sigma}^{-1}$の導出について考える。
$D$行$D$列の分散共分散行列の$i$番目の固有値を$\lambda_i$、それに対応する大きさ1の固有ベクトルを$\mathbf{u}_i \quad (i=1,2, \cdots ,D)$と表すとする。このとき、固有値・固有ベクトルの定義より下記が成立する。
$$
\large
\begin{align}
\mathbf{\Sigma} \mathbf{u}_i = \lambda_i \mathbf{u}_i
\end{align}
$$

上記に左から$\mathbf{\Sigma}^{-1}$をかけると下記のようになる。
$$
\large
\begin{align}
\mathbf{\Sigma}^{-1}\mathbf{\Sigma} \mathbf{u}_i &= \mathbf{\Sigma}^{-1} \lambda_i \mathbf{u}_i \\
\mathbf{u}_i &= \lambda_i \mathbf{\Sigma}^{-1} \mathbf{u}_i
\end{align}
$$

上記の右辺の計算にあたって、$\lambda_i$と$\mathbf{\Sigma}^{-1}$の順番を入れ替えたが、これは$\lambda_i$がスカラー値であるからである。次に上記の両辺に右から$\mathbf{u}_i^{\mathrm{T}}$をかけ、スカラー$\lambda_i$でわると下記のようになる。
$$
\large
\begin{align}
\frac{1}{\lambda_i} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} = \mathbf{\Sigma}^{-1} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} \quad (3)
\end{align}
$$

ここで$\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}}$について考えると下記のように計算できる。
$$
\large
\begin{align}
\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} &= \left(\begin{array}{c} u_{i1} \\ \vdots \\ u_{iD} \end{array} \right) \left(\begin{array}{r} u_{i1} & \cdots & u_{iD} \end{array} \right) \\
&= \left(\begin{array}{ccc} u_{i1}^2 & \cdots & u_{i1}u_{iD} \\ \vdots & \ddots & \vdots \\ u_{iD}u_{i1} & \cdots & u_{iD}^2 \end{array} \right) \quad (4)
\end{align}
$$

また、$\mathbf{U}^{\mathrm{T}}\mathbf{U}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{U}^{\mathrm{T}}\mathbf{U} &= \left(\begin{array}{ccc} u_{11} & \cdots & u_{D1} \\ \vdots & \ddots & \vdots \\ u_{1D} & \cdots & u_{DD} \end{array} \right)\left(\begin{array}{ccc} u_{11} & \cdots & u_{1D} \\ \vdots & \ddots & \vdots \\ u_{D1} & \cdots & u_{DD} \end{array} \right) \\
&= \left(\begin{array}{ccc} \displaystyle \sum_{i=1}^{D} u_{i1}^2 & \cdots & \displaystyle \sum_{i=1}^{D} u_{i1}u_{iD} \\ \vdots & \ddots & \vdots \\ \displaystyle \sum_{i=1}^{D} u_{iD}u_{i1} & \cdots & \displaystyle \sum_{i=1}^{D} u_{iD}^2 \end{array} \right) = \left(\begin{array}{ccc} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{array} \right) \quad (5)
\end{align}
$$

$(4)$式、$(5)$式の対角成分などを見比べることで、下記が成立することがわかる。
$$
\large
\begin{align}
\sum_{i=1}^{D} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} &= \left(\begin{array}{ccc} \displaystyle \sum_{i=1}^{D} u_{i1}^2 & \cdots & \displaystyle \sum_{i=1}^{D} u_{i1}u_{iD} \\ \vdots & \ddots & \vdots \\ \displaystyle \sum_{i=1}^{D} u_{iD}u_{i1} & \cdots & \displaystyle \sum_{i=1}^{D} u_{iD}^2 \end{array} \right) \\
&= \mathbf{U}^{\mathrm{T}}\mathbf{U} \\
&= \left(\begin{array}{ccc} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{array} \right) \quad (6)
\end{align}
$$

$(6)$式を元に$(3)$式に適用することで、下記のように導出することができる。
$$
\large
\begin{align}
\sum_{i=1}^{D} \frac{1}{\lambda_i} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} &= \sum_{i=1}^{D} \mathbf{\Sigma}^{-1} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} \\
&= \mathbf{\Sigma}^{-1} \sum_{i=1}^{D} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} \\
&= \mathbf{\Sigma}^{-1} \mathbf{U}^{\mathrm{T}}\mathbf{U} \\
&= \mathbf{\Sigma}^{-1} \mathbf{I} \\
&= \mathbf{\Sigma}^{-1}
\end{align}
$$

上記より、$\mathbf{\Sigma}^{-1}$は下記のように表すことができる。
$$
\large
\begin{align}
\mathbf{\Sigma}^{-1} = \sum_{i=1}^{D} \frac{1}{\lambda_i} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} \quad (7)
\end{align}
$$

固有ベクトルを用いた基底の変換

$(2)$では下記のように多変数正規分布の確率密度関数について表した。
$$
\large
\begin{align}
N(x|\mathbf{\mu}, \mathbf{\Sigma}) = \frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} \exp \left( -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu}) \right)
\end{align}
$$

ここで上記の指数関数の中に着目し、下記のように$\Delta^2$を考える。
$$
\large
\begin{align}
\Delta^2 = (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu})
\end{align}
$$

上記に$(7)$式を代入すると下記のようになる。
$$
\large
\begin{align}
\Delta^2 &= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \Sigma^{-1}(\mathbf{x}-\mathbf{\mu}) \\
&= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \sum_{i=1}^{D} \frac{1}{\lambda_i} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu}) \\
&= \sum_{i=1}^{D} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i} \quad (8)
\end{align}
$$

上記の式で$(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i$と$\mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})$はどちらもベクトル$\mathbf{x}-\mathbf{\mu}$からベクトル$\mathbf{u}_i$への正射影を意味するので、これを$y_i$とおく。これは下記のような式で表すことができる。
$$
\large
\begin{align}
y_i = (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i = \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu}) \quad (9)
\end{align}
$$

$(8)$式と$(9)$式より、$\Delta^2$は下記のように表せる。
$$
\large
\begin{align}
\Delta^2 &= \sum_{i=1}^{D} \frac{(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{x}-\mathbf{\mu})}{\lambda_i} \\
&= \sum_{i=1}^{D} \frac{y_i^2}{\lambda_i} \quad (10)
\end{align}
$$

$(10)$式は固有ベクトルへの正射影に対応する値を$\sqrt{\lambda_i}$でわった値を元に平均ベクトル$\mu$からの距離を考えていると解釈できる。この二次形式$\Delta^2$はマハラノビス距離(Mahalanobis distance)と呼ばれており、固有値が大きい方向の差の評価を少なくする一方で固有値が小さい方向の差の評価を大きくする処理を行なっていると考えればわかりやすい。

また、ここで下記のように$\mathbf{y}$、$\mathbf{U}$を定義する。
$$
\large
\begin{align}
\mathbf{y} = \left(\begin{array}{c} y_{1} \\ \vdots \\ u_{D} \end{array} \right)
\end{align}
$$
$$
\large
\begin{align}
\mathbf{U} = \left(\begin{array}{c} \mathbf{u}_1^{\mathrm{T}} \\ \vdots \\ \mathbf{u}_D^{\mathrm{T}} \end{array} \right)
\end{align}
$$

上記と$(9)$式より、$\mathbf{y}$は下記のように表すことができる。
$$
\large
\begin{align}
\mathbf{y} = \mathbf{U} (\mathbf{x}-\mathbf{\mu})
\end{align}
$$

これは分散共分散行列の固有ベクトルに基づく直交行列を用いて、$\mathbf{x}-\mathbf{\mu}$の基底を変換することを意味している。

二次形式(Mahalanobis distance)の図形的理解

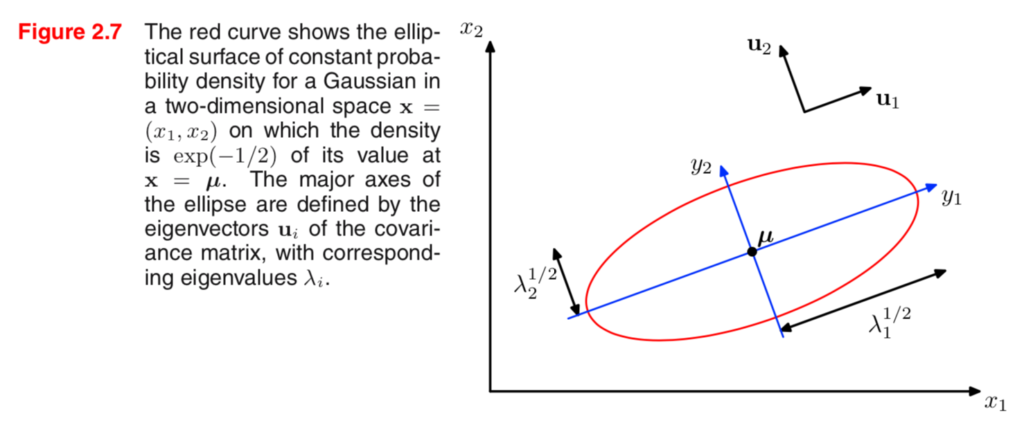
図形的理解は上記を元に行うと良い。分散共分散行列の固有ベクトル方向に基底を変換し、かつ、固有値が大きい方向の差の評価を小さくするような計算を行う。
$$
\large
\begin{align}
\Delta^2 = \sum_{i=1}^{D} \frac{y_i^2}{\lambda_i} \quad (10)と同じ
\end{align}
$$

図と上記で表した$(10)$式を見比べて理解することで、多変量正規分布における確率密度関数の取り扱いについて確認すると良いと思われる。

PCAとの関連

PCAは分散共分散行列の最大の固有値に対応する固有ベクトルが、最もサンプルの分散が大きい方向となりこれを主成分と考えて次元の削減の処理を行うなどの手法である。PCAについて詳しくは下記に取りまとめた。
https://www.hello-statisticians.com/explain-terms-cat/pca1.html

まとめ

多次元正規分布の確率密度関数の理解にあたっては、指数関数の中について理解ができれば$1$次元の正規分布と同様に理解することができる。山の等高線のように確率密度関数を考えることで、概ね理解できると思われる。