「統計検定$2$級 公式問題集 CBT対応版」の解答例を取りまとめるにあたって、当記事では「PART.$2$ 分野・項目別 問題・解説」のCategory.$1$「$1$変数記述統計」の解答例を作成しました。解答例は「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
解答例
Q.1
相対度数表の定義より、それぞれ下記のように計算できる。
ア)
$$
\large
\begin{align}
100 – (85.1+2.1) = 12.8
\end{align}
$$
イ)
$$
\large
\begin{align}
100 – (76.6+17.0+2.1) = 4.3
\end{align}
$$
よって、正解は⑤である。
Q.2
累積相対度数を考えればよい。
| 階級 | 相対度数(%) | 累積相対度数(%) |
| 〜$100$ | $13.2$ | $13.2$ |
| $100$〜$200$ | $7.2$ | $20.4$ |
| $200$〜$300$ | $7.0$ | $27.4$ |
| $300$〜$400$ | $6.1$ | $33.5$ |
| $400$〜$500$ | $5.6$ | $39.1$ |
| $500$〜$600$ | $5.5$ | $44.6$ |
| $600$〜$700$ | $4.5$ | $49.1$ |
| $700$〜$800$ | $4.2$ | $53.3$ |
上記より、正解は①である。
Q.3
東京の箱ひげ図には$16$〜$18$度のサンプルが$2$つあるが、$(A)$のみが対応する。よって正解は①である。
Q.4
① 最高得点は$90$点であるので×
② 最低得点は$40$点であるので×
③ 正しい
④ 上位$20$%の最低得点は$78$点であるので×
⑤ 最頻値は$58$点であるので×
上記より正解は③である。
Q.5
Ⅰ 傾向変動は長期の動きであるが、常に直線であるとは限らないので×
Ⅱ 正しい
Ⅲ 不規則変動は傾向変動と季節変動以外の変動を指すので、予測が困難な偶然運動も含むので×
上記より正解は②である。
Q.6
平均変化率$r$に関して下記が成立する。
$$
\large
\begin{align}
102.6 \left( 1+\frac{r}{100} \right)^3 &= 105.6 \\
1+\frac{r}{100} &= \left( \frac{105.6}{102.6} \right)^{\frac{1}{3}} \\
r &= 100 \left[ \left( \frac{105.6}{102.6} \right)^{\frac{1}{3}} – 1 \right]
\end{align}
$$
上記より正解は④である。
Q.7
$\overline{F}$は下記のように計算できる。
$$
\large
\begin{align}
\overline{F} &= 1.8 \overline{C} + 32 \\
&= 1.8 \times 2.4 + 32 \\
&= 36.32
\end{align}
$$
また、$s_F$は下記のように計算できる。
$$
\large
\begin{align}
s_F &= \sqrt{\frac{1}{16} \sum_{i=1}^{17}((1.8C_i+32)-(1.8\overline{C}-32))^2} \\
&= \sqrt{\frac{1.8^2}{16} \sum_{i=1}^{17}(C_i-\overline{C})^2} \\
&= \sqrt{1.8^2 \times 7^2} \\
&= 1.8 \times 7 \\
&= 12.6
\end{align}
$$
上記より正解は④である。
Q.8
累積相対度数は下記を実行することで作成できる。
import numpy as np
x = np.array([[5.4, 10.7, 16.3, 24.1, 43.5], [5.1, 10.3, 15.4, 22.7, 46.4], [8.7, 14.3, 17.8, 23.0, 36.2], [5.2, 9.8, 14.9, 22.3, 47.9], [8.4, 13.1, 17.2, 22.7, 38.6]])
print(np.cumsum(x,axis=1))・実行結果
array([[ 5.4, 16.1, 32.4, 56.5, 100. ],
[ 5.1, 15.4, 30.8, 53.5, 99.9],
[ 8.7, 23. , 40.8, 63.8, 100. ],
[ 5.2, 15. , 29.9, 52.2, 100.1],
[ 8.4, 21.5, 38.7, 61.4, 100. ]])また、ローレンツ曲線は下記を実行することで得られる。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[5.4, 10.7, 16.3, 24.1, 43.5], [5.1, 10.3, 15.4, 22.7, 46.4], [8.7, 14.3, 17.8, 23.0, 36.2], [5.2, 9.8, 14.9, 22.3, 47.9], [8.4, 13.1, 17.2, 22.7, 38.6]])
x_cum = np.zeros([x.shape[0],x.shape[0]+1])
x_cum[:,1:] = np.cumsum(x,axis=1)
nation_label = ["JPN", "USA", "SWE", "CHN", "DEU"]
for i in range(x_cum.shape[0]):
plt.plot(np.arange(6),x_cum[i,:],label=nation_label[i])
plt.legend(loc="upper left")
plt.show()・実行結果
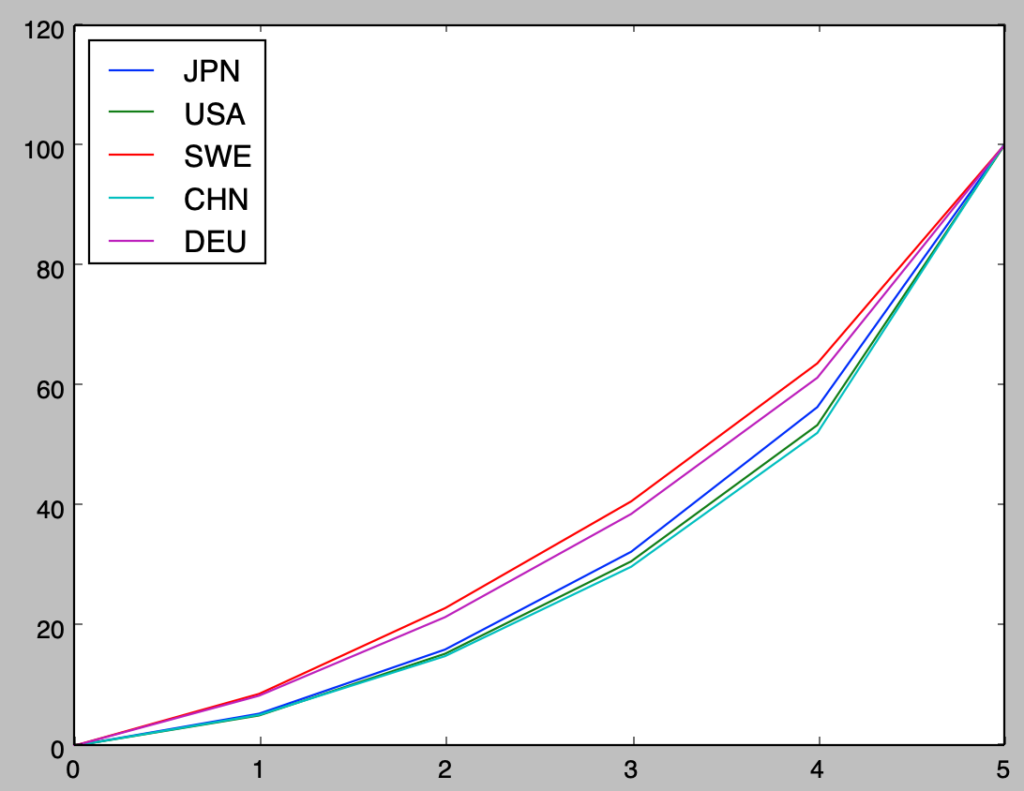
上記より、下記のように考えることができる。
Ⅰ 完全平等線は$(0,0)$と$(5,100)$を通る直線なので、いずれの国のローレンツ曲線も完全平等線の下に弧を描く。よって正しい。
Ⅱ ジニ係数は完全平等線とローレンツ曲線の間の面積に対応するので、アメリカ>日本>ドイツである。よって正しくない。
Ⅲ 中国のローレンツ曲線はスウェーデンのローレンツ曲線の下を通る。よって正しい。
したがって、正解は⑤である。
Q.9
$12n$か月ごとに正の相関と$12n+6$か月ごとに負の相関があることから正解は②である。ACFはAuto Correlatino Functionの略であり、自己相関係数に対応することは抑えておくと良い。
Q.10
基準年の第$i$財の価格を$p_{0i}$、購入数量を$q_{0i}$、対象年の第$i$財の価格を$p_{ti}$、購入数量を$q_{ti}$とおく。このとき「対象年に基準年と同じ購入量を購入した場合の総購入金額の比率」を表すラスパイレス価格指数$L_{t}$は下記のように定義される。
$$
\large
\begin{align}
L_{t} = \frac{\displaystyle \sum_{i=1}^{n} p_{ti} q_{0i}}{\displaystyle \sum_{i=1}^{n} p_{0i} q_{0i}} \times 100
\end{align}
$$
上記の定義に対応するのが②であるので、正解は②である。また、計算結果は$107.6$であり、平均価格が上昇したと考えることができる。
・考察
ラスパイレス指数は「価格の調査は標本抽出を元に行うことができコストがそれほどかからないが、数量調査は全数調査が必要でありコストがかかる」ことから、広く用いられることが多いと抑えておくと良いです。
参考
・【統計検定$2$級対応】統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

[…] 統計検定$2$級 公式問題集 CBT対応版 Q.$1.8$より […]