当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.2.2$節「ローレンツ曲線」の内容を元に経済などの分野でよく用いられるローレンツ曲線とジニ係数の概要に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
ローレンツ曲線・ジニ係数の概要
概要
ローレンツ曲線(Lorenz curve)はM.O.ローレンツが考案した「所得などの量の集中度や格差を表すグラフ」です。ローレンツ曲線は下記のようなグラフで表されます。
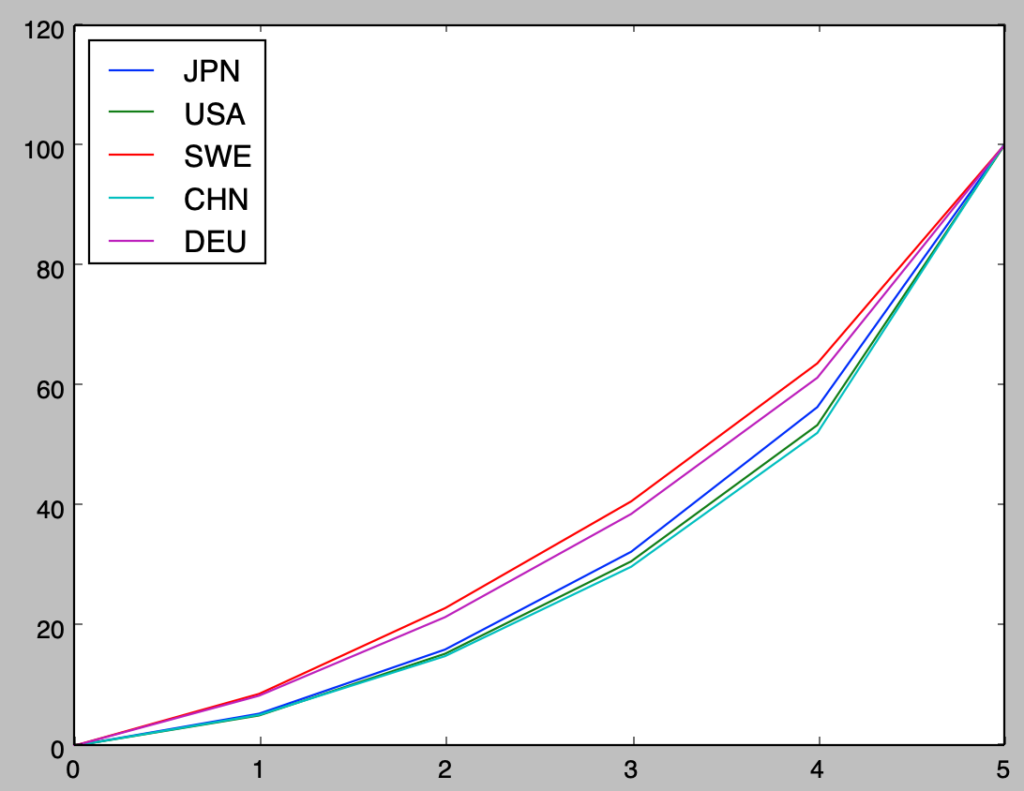
上図は日本、アメリカ、スウェーデン、中国、ドイツの$5$か国の五分位所得割合に基づくローレンツ曲線を表したものです。ローレンツ曲線は上にいくほど「平等」で下にいくほど「不平等」であることを表します。図ではスウェーデン、ドイツ、日本、アメリカ、中国の順で平等であることが読み取れます。
ジニ係数(Gini’s coefficient)はグラフの$(0,0)$と$(5,100)$を通る直線とそれぞれのローレンツ曲線の間の面積の$2$倍で定義される指標であり、ジニ係数が大きいほど「不平等」であると考えられます。なお、グラフは$2011$〜$2014$年を元に作成されているので、その点には注意が必要です。
必要な数学
ジニ係数は「完全平等曲線」と「ローレンツ曲線」の間の面積の$2$倍で定義されるので、積分の定義や台形公式に基づく数値積分の基本的な計算法に関しては抑えておくと良いです。
ローレンツ曲線とジニ係数
ローレンツ曲線
ローレンツ曲線の描画にあたっては、まず所得の順に家計を並べ、世帯数を元に五等分します。たとえば$1$億世帯ある場合は所得の順に$1$億世帯をソートし、$2,000$万世帯ずつで五等分を行います。このときにそれぞれの$2,000$万世帯ずつが全体の所得に占める割合を計算します。計算結果は度数分布表と同様の要領で、表で表すことが可能です。前節で確認したローレンツ曲線に対応する表を作成すると、下記のように表せます。
| 階級 | 第$1$階級 | 第$2$階級 | 第$3$階級 | 第$4$階級 | 第$5$階級 |
| 日本 | $5.4$ | $10.7$ | $16.3$ | $24.1$ | $43.5$ |
| アメリカ | $5.1$ | $10.3$ | $15.4$ | $22.7$ | $46.4$ |
| スウェーデン | $8.7$ | $14.3$ | $17.8$ | $23.0$ | $36.2$ |
| 中国 | $5.2$ | $9.8$ | $14.9$ | $22.3$ | $47.9$ |
| ドイツ | $8.4$ | $13.1$ | $17.2$ | $22.7$ | $38.6$ |
上記の表を確認するにあたっては、どの行も「左から右にいくにつれて数字が必ず大きくなる」という点は抑えておく必要があります。このことは元々所得の順にソートを行なった上でグループ分けし、割合を計算したことを鑑みれば必然です。
次に「確率の累積」を左から順に計算します。左から「第$1$階級の数字」、「第$1$階級の数字+第$2$階級の数字」〜「第$1$階級の数字+第$2$階級の数字+$\cdots$+第$5$階級の数字」の数字を並べます。五カ国の例に基づいて計算すると下記のような結果が得られます。
| 階級 | 第$1$階級 | 第$2$階級 | 第$3$階級 | 第$4$階級 | 第$5$階級 |
| 日本 | $5.4$ | $16.1$ | $32.4$ | $56.5$ | $100$ |
| アメリカ | $5.1$ | $15.4$ | $30.8$ | $53.5$ | $99.9$ |
| スウェーデン | $8.7$ | $23$ | $40.8$ | $63.8$ | $100$ |
| 中国 | $5.2$ | $15$ | $29.9$ | $52.2$ | $100.1$ |
| ドイツ | $8.4$ | $21.5$ | $38.7$ | $61.4$ | $100$ |
上記を元にローレンツ曲線の描画を行うことができます。累積を計算するので一番右の列は$100$に近い値になりますが、有効数字や四捨五入を行う都合上、必ずしも$100$に一致しないことにも注意が必要です。一連の流れは下記を実行することでグラフを描くことができます。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[5.4, 10.7, 16.3, 24.1, 43.5], [5.1, 10.3, 15.4, 22.7, 46.4], [8.7, 14.3, 17.8, 23.0, 36.2], [5.2, 9.8, 14.9, 22.3, 47.9], [8.4, 13.1, 17.2, 22.7, 38.6]])
x_cum = np.zeros([x.shape[0],x.shape[0]+1])
x_cum[:,1:] = np.cumsum(x,axis=1)
nation_label = ["JPN", "USA", "SWE", "CHN", "DEU"]
for i in range(x_cum.shape[0]):
plt.plot(np.arange(6),x_cum[i,:],label=nation_label[i])
plt.legend(loc="upper left")
plt.show()・実行結果

ジニ係数
ジニ係数は全世帯が平等である場合の完全平等線(complete equality line)とローレンツ曲線の間の面積の$2$倍に対応します。下記を実行することで前項の例に完全平等線を追加することができます。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[5.4, 10.7, 16.3, 24.1, 43.5], [5.1, 10.3, 15.4, 22.7, 46.4], [8.7, 14.3, 17.8, 23.0, 36.2], [5.2, 9.8, 14.9, 22.3, 47.9], [8.4, 13.1, 17.2, 22.7, 38.6]])
x_cum = np.zeros([x.shape[0],x.shape[0]+1])
x_cum[:,1:] = np.cumsum(x,axis=1)
nation_label = ["JPN", "USA", "SWE", "CHN", "DEU"]
for i in range(x_cum.shape[0]):
plt.plot(np.arange(6)/5.,x_cum[i,:]/100.,label=nation_label[i])
plt.plot(np.array([0.,1.]), np.array([0., 1.]), color="black",label="equality line")
plt.legend(loc="upper left")
plt.show()・実行結果
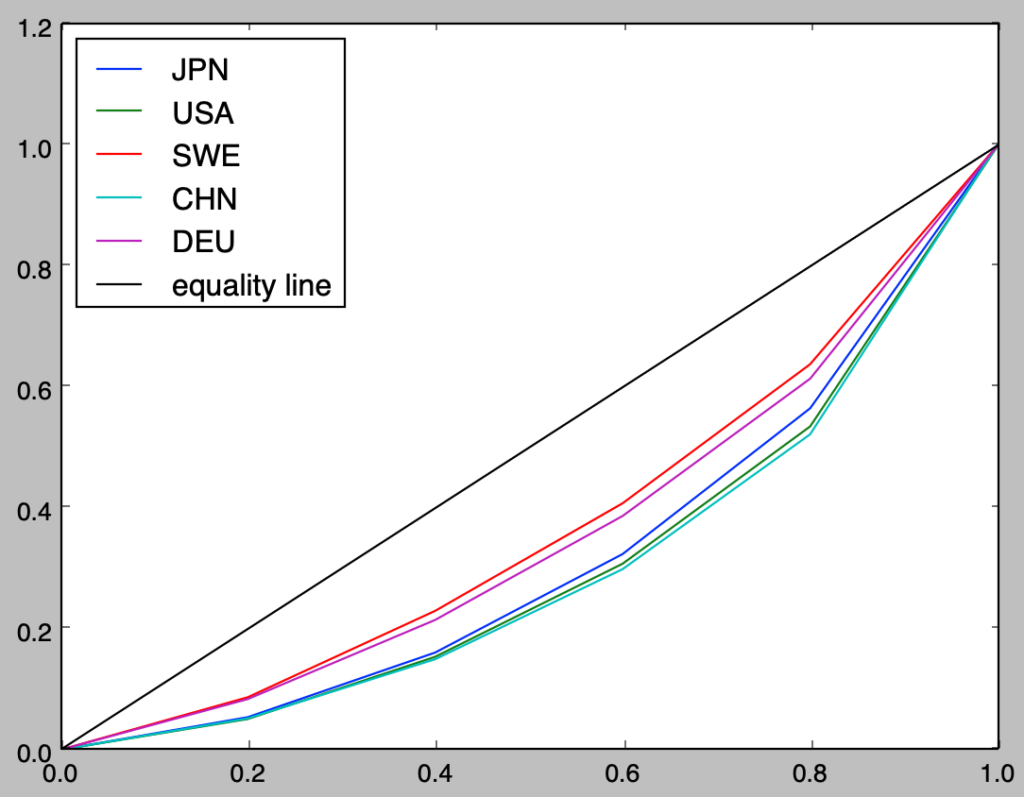
上図のようなローレンツ曲線を元に「不平等」かどうかを論じることができますが、前項の表では第$1$階級では相対確率がアメリカ<中国である一方で、それ以外ではアメリカ>中国が成立するなど、取り扱いが難しい場合があります。
このような場合に面積に基づいて定量化を行うジニ係数のような指標があると用いやすいです。各国のジニ係数は台形公式に基づいて下記のような処理を行うことで計算することができます。
import numpy as np
x = np.array([[5.4, 10.7, 16.3, 24.1, 43.5], [5.1, 10.3, 15.4, 22.7, 46.4], [8.7, 14.3, 17.8, 23.0, 36.2], [5.2, 9.8, 14.9, 22.3, 47.9], [8.4, 13.1, 17.2, 22.7, 38.6]])
x_cum = np.zeros([x.shape[0],x.shape[0]+1])
x_cum[:,1:] = np.cumsum(x,axis=1)/100.
s = np.repeat(1.*1./2.,5)
for i in range(x.shape[1]):
s -= 0.2*(x_cum[:,i]+x_cum[:,i+1])/2.
Gini = 2*s
print(Gini)・実行結果
[ 0.3584 0.381 0.2548 0.3906 0.28 ]上記より、ジニ係数を大きい順に並べると、「中国」、「アメリカ」、「日本」、「ドイツ」、「スウェーデン」であることが確認できます。
