上記の「確率分布(probability distribution)①」で取り扱えなかった確率分布に関する演習を以下では取り扱いました。
・標準演習$100$選
https://www.hello-statisticians.com/practice_100
離散型確率分布
超幾何分布と母分散の有限修正
・問題
$N$個のサンプルが$2$つのグループで構成されており、グループ$1$が$M$個、グループ$2$が$N-M$個あると仮定する。このとき、$n$個の標本の無作為抽出を考える際に、$N$が有限であるならば一度抽出を行なった標本を戻すか戻さないかによって取り扱いが変わることに注意が必要である。
具体的には抽出を行なった標本を戻した上で次の抽出を行う「復元抽出」と戻さないで抽出を行う「非復元抽出」があるが、「復元抽出」が二項分布で表される一方で、「非復元抽出」は超幾何分布で表される。
以下では「非復元抽出」に関して取り扱う「超幾何分布」の確率関数や期待値$E[Y]$、分散$V[Y]$の導出、さらに二項分布の分散との対応から「母分散の有限修正(finite correction)」に関して取り扱う。下記の問いにそれぞれ答えよ。
i)
$M$個のグループ$1$の標本と$N-M$個のグループ$2$の標本から構成される$N$個から$n$個の「非復元無作為抽出」を行う際にグループ$1$が抽出された個数を確率変数の$Y$で表すとき、確率関数$p(y)=P(Y=y)$を表せ。ただし$\max(0,n-(N-M)) \leq y \leq \min(n,M)$を仮定して良い。
ⅱ)
i)で用いた「$\max(0,n-(N-M)) \leq y \leq \min(n,M)$」の仮定に関して簡単に解釈せよ。
ⅲ)
$i$回目の抽出でグループ$1$を引いた場合に$X_i=1$、グループ$2$を引いた場合に$X_i=0$のように確率変数$X_i$を定義する。このとき確率変数$Y$は$Y = X_1 + X_2 + \cdots + X_n$のように表せる。$X_i$に関して$E[X_i], E[X_i^2]$を答えよ
iv)
ⅲ)で定めた$X_i$を元に$E[X_iX_j], \, i \neq j$を表せ。
v)
$V[X_i]=E[X_i^2]-E[X_i]^2, \, \mathrm{Cov}(X_i,X_j)=E[X_iX_j]-E[X_i]E[X_j]$を用いて$V[X_i], \mathrm{Cov}(X_i,X_j)$を計算せよ。
vi)
$E[Y] = E[X_1 + X_2 + \cdots + X_n]$を元に超幾何分布の期待値$E[Y]$を計算せよ。
vⅱ)
$V[Y] = V[X_1 + X_2 + \cdots + X_n]$を元に超幾何分布の分散$V[Y]$を計算せよ。
vⅲ)
「復元抽出」の場合は二項分布を元に考えることができるが、$Z \sim \mathrm{Bin}(n,p)$の分散を$V[Z]$とおくと$V[Z]=np(1-p)$のように表せる。ここで$p=M/N$のように表すとき、$V[Y]/V[Z]$を計算せよ。
・解答
i)
確率関数$p(y)=P(Y=y)$は下記のように表すことができる。
$$
\large
\begin{align}
p(y) = \frac{{}_{M} C_{y} {}_{N-M} C_{n-y}}{{}_{N} C_{n}}
\end{align}
$$
ⅱ)
$y \leq \min(n,M)$は「グループ$1$を抽出する個数$y$」が「抽出する個数$n$」と「グループ$1$の個数$M$個」のどちらも上回らないことを表す。$\max(0,n-(N-M)) \leq y$は「グループ$1$を抽出する個数$y$」が「$0$以上」かつ「グループ$2$の個数$N-M$個が$n$より少なくなる際の$y$の下限値が$n-(N-M)$」であることを表す。$y \leq \min(n,M)$と$\max(0,n-(N-M)) \leq y$の数式は特にグループ$1$と$2$の数に偏りがある場合や$n$がそれなりに大きい場合に注意が必要である。
ⅲ)
$E[X_i], E[X_i^2]$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
E[X_i] &= 0 \cdot P(X_i=0) + 1 \cdot P(X_i=1) \\
&= P(X_i=1) \\
&= \frac{M}{N} \\
E[X_i^2] &= 0^2 \cdot P(X_i=0) + 1^2 \cdot P(X_i=1) \\
&= P(X_i=1) \\
&= \frac{M}{N}
\end{align}
$$
iv)
$i \neq j$のとき、$E[X_iX_j]$は下記のように表せる。
$$
\large
\begin{align}
E[X_iX_j] &= 0 \cdot (P(X_i=0,X_j=0)+P(X_i=1,X_j=0)+P(X_i=0,X_j=1)) + 1 \cdot P(X_i=1,X_j=1) \\
&= P(X_i=1,X_j=1) \\
&= \frac{M(M-1)}{N(N-1)}
\end{align}
$$
v)
$V[X_i], \mathrm{Cov}(X_i,X_j)$は下記のように計算できる。
$$
\large
\begin{align}
V[X_i] &= E[X_i^2] – E[X_i]^2 \\
&= \frac{M}{N} – \left( \frac{M}{N} \right)^2 \\
&= \frac{M(N-M)}{N^2} \\
\mathrm{Cov}(X_i,X_j) &= E[X_iX_j] – E[X_i]E[X_j] \\
&= \frac{M(M-1)}{N(N-1)} – \frac{M^2}{N^2} \\
&= \frac{MN(M-1)}{N^2(N-1)} – \frac{M^2(N-1)}{N^2(N-1)} \\
&= \frac{\cancel{M^2N} – MN – \cancel{M^2N} + M^2}{N^2(N-1)} \\
&= -\frac{M(N-M)}{N^2(N-1)}
\end{align}
$$
vi)
超幾何分布の期待値$E[Y]$は下記のように計算できる。
$$
\large
\begin{align}
E[Y] &= E[X_1 + X_2 + \cdots + X_n] \\
&= nE[X_i] \\
&= \frac{nM}{N}
\end{align}
$$
vⅱ)
超幾何分布の分散$V[Y]$は下記のように計算できる。
$$
\large
\begin{align}
V[Y] &= V[X_1 + X_2 + \cdots + X_n] \\
&= nV[X_i] + 2 \cdot {}_{n} C_{2} \mathrm{Cov}(X_i,X_j) \\
&= nV[X_i] + n(n-1) \mathrm{Cov}(X_i,X_j) \\
&= \frac{nM(N-M)}{N^2} – \frac{n(n-1)M(N-M)}{N^2(N-1)} \\
&= \frac{nM(N-M)}{N^2(N-1)} [(N-\cancel{1})-(n-\cancel{1})] \\
&= \frac{nM(N-M)(N-n)}{N^2(N-1)} \\
&= n \cdot \frac{M}{N} \left( 1-\frac{M}{N} \right) \times \frac{N-n}{N-1}
\end{align}
$$
vⅲ)
$V[Z]=np(1-p)$に$p=M/N$を代入することで下記が得られる。
$$
\large
\begin{align}
V[Z] &= np(1-p) \\
&= n \cdot \frac{M}{N} \left( 1-\frac{M}{N} \right)
\end{align}
$$
よって$V[Y]/V[Z]$は下記のように考えることができる。
$$
\large
\begin{align}
\frac{V[Y]}{V[Z]} = \frac{N-n}{N-1}
\end{align}
$$
・解説
「統計検定準$1$級対応 ワークブック」の問題$5.3$を元に作成を行いました。vⅱ)の計算では$V[X_1 + X_2 \cdots X_n]$の計算にあたって、共分散の$\mathrm{Cov}(X_i,X_j)$を考える必要があることに注意が必要です。詳しくは下記などを確認すると良いと思います。
また、vⅲ)の答えが有限修正(finite correction)の際の項に一致することは確認しておくと良いです。
重複組合せと負の二項分布
・問題
負の二項分布$NB(r,p)$は確率$p$の事象$1$が$r$回起こるまでに$(1-p)$の事象$2$が$Y$回起こると考える場合の$Y$の分布であり、$Y=y$回起こる確率を表す確率関数を$p(y)$とおくと、$p(y)$は下記のように表すことができる。
$$
\large
\begin{align}
p(y) &= {}_{r} H_{y} p^{r} (1-p)^{y}, \quad y=0,1,2, \cdots \\
{}_r H_{y} &= {}_{y+r-1} C_{y} = \frac{(y+r-1)(y+r-2) \cdots (r+1)r}{y!}
\end{align}
$$
以下では上記の重複組合せ${}_{r} H_{y}$や確率関数の理解と、幾何分布の期待値$E[X_i]$と分散$V[X_i]$を用いて$NB(r,p)$の期待値$E[Y]$と分散$V[Y]$の導出を行う。下記の問いにそれぞれ答えよ。
i) 重複組合せ${}_{r} H_{y}$は「$r$種類のものを重複して$y$個選ぶ際の選び方」とされるが、${}_{r} H_{y}$が${}_{r+y-1} C_{y}$に一致することを下図などを用いることで簡単に解説せよ。
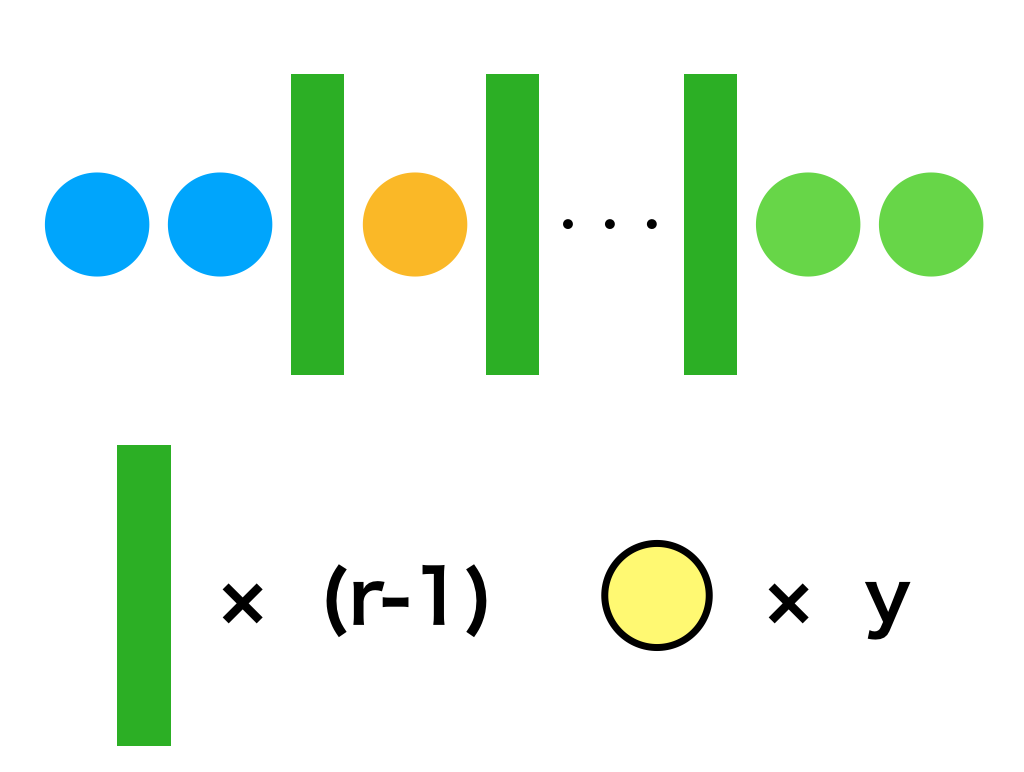
ⅱ) 整数$a$と$0$以上の整数$b$に対し、二項係数の一般化を下記のように定める。
$$
\begin{align}
\left(\begin{array}{c} a \\ b \end{array} \right) \equiv \frac{a(a-1) \cdots (a-b+1)}{b!}
\end{align}
$$
このとき下記が成立することを示せ。
$$
\begin{align}
{}_{r} H_{y} = (-1)^{y} \left(\begin{array}{c} -r \\ y \end{array} \right)
\end{align}
$$
ⅲ) $p=0.5, r=3$のとき、確率関数$p(y)$を元に$p(0), p(1), p(2), p(3), p(4), p(5)$をそれぞれ計算せよ。
iv) 確率$p$の事象が$X_i$回目に起こると考えるとき、幾何分布$\mathrm{Geo}(p)$に基づいて期待値$E[X_i], V[X_i]$は下記のように表すことができる。
$$
\begin{align}
E[X_i] &= \frac{1}{p} \\
V[X_i] &= \frac{1-p}{p^2}
\end{align}
$$
ここで$\displaystyle Y = \sum_{i=1}^{r} X_i, Y \sim \mathrm{NB}(r,p)$であることに基づいて負の二項分布$\mathrm{NB}(r,p)$の期待値$E[Y]$を計算せよ。
v) $\displaystyle Y = \sum_{i=1}^{r} X_i, Y \sim \mathrm{NB}(r,p)$であることに基づいて負の二項分布$\mathrm{NB}(r,p)$の分散$V[Y]$を計算せよ。
・解答
i)
図を元に「○」と「|」の並べ替え方の総数が重複組合せの定義に一致することが確認できる。
ⅱ)
下記のように導出を行うことができる。
$$
\large
\begin{align}
{}_r H_{y} &= {}_{y+r-1} C_{y} \\
&= \frac{(y+r-1)(y+r-2) \cdots (r+1)r}{y!} \\
&= \frac{r(r+1) \cdots (r+y-2)(r+y-1)}{y!} \\
&= (-1)^{y} \frac{(-r)(-r-1) \cdots (-r-y+2)(-r-y+1)}{y!} \\
&= (-1)^{y} \left(\begin{array}{c} -r \\ y \end{array} \right)
\end{align}
$$
ⅲ)
下記のようにそれぞれ計算できる。
$$
\large
\begin{align}
p(0) &= {}_{3} H_{0} 0.5^3(1-0.5)^0 \\
&= {}_{3+0-1} C_{0} 0.5^3 = 0.125 \\
p(1) &= {}_{3} H_{1} 0.5^3(1-0.5)^1 \\
&= {}_{3+1-1} C_{1} 0.5^4 = 3 \cdot 0.5^4 \simeq 0.188 \\
p(2) &= {}_{3} H_{2} 0.5^3(1-0.5)^2 \\
&= {}_{3+2-1} C_{2} 0.5^5 = 6 \cdot 0.5^5 \simeq 0.188 \\
p(3) &= {}_{3} H_{3} 0.5^3(1-0.5)^3 \\
&= {}_{3+3-1} C_{3} 0.5^6 = 10 \cdot 0.5^6 \simeq 0.156 \\
p(4) &= {}_{3} H_{4} 0.5^3(1-0.5)^4 \\
&= {}_{3+4-1} C_{3} 0.5^7 = 15 \cdot 0.5^7 \simeq 0.117 \\
p(5) &= {}_{3} H_{5} 0.5^3(1-0.5)^5 \\
&= {}_{3+5-1} C_{5} 0.5^8 = 21 \cdot 0.5^7 \simeq 0.082
\end{align}
$$
iv)
確率変数$\displaystyle Y = \sum_{i=1}^{r} (X_i-1)$に関して下記が成立する。
$$
\large
\begin{align}
E[Y] &= E \left[ \sum_{i=1}^{r} (X_i-1) \right] = E \left[ -r + \sum_{i=1}^{r} X_i \right] \\
&= – r + \sum_{i=1}^{r} E[X_i] \\
&= -r+\frac{r}{p} = \frac{r(1-p)}{p}
\end{align}
$$
v)
確率変数$\displaystyle Y = \sum_{i=1}^{r} (X_i-1)$に関して下記が成立する。
$$
\large
\begin{align}
V[Y] &= V \left[ \sum_{i=1}^{r} (X_i-1) \right] = V \left[ -r + \sum_{i=1}^{r} X_i \right] \\
&= 0 + \sum_{i=1}^{r} V[X_i] \\
&= \frac{r(1-p)}{p^2}
\end{align}
$$
・解説
ⅲ)の計算結果に関して$p(0)+p(1)+p(2)=0.5$が成立することが確認できますが、$3$本先取で$3$勝$0$敗〜$3$勝$2$敗の確率の和に対応させると結果が妥当であると解釈できます。
多項分布
・問題
$2$項分布では確率変数$X$が$0, 1$の$2$値を取る場合を取り扱うが、$Y$が$K \leq 2$の$K$値を取るように拡張したときに確率変数ベクトル$Y$が従う分布が多項分布である。
$$
\large
\begin{align}
X_{n} &= \left(\begin{array}{cc} X_{n1} \\ \vdots \\ X_{nK} \end{array} \right) \quad (1) \\
Y &= \left(\begin{array}{cc} Y_{1} \\ \vdots \\ Y_K \end{array} \right) = \left(\begin{array}{cc} \displaystyle \sum_{n=1}^{N} X_{n1} \\ \vdots \\ \displaystyle \sum_{n=1}^{N} X_{nK} \end{array} \right) \quad (2) \\
\sum_{k=1}^{K} X_{nk} &= 1, \quad \sum_{k=1}^{K} Y_k = n
\end{align}
$$
二項分布では$n$回の試行それぞれで$X=1$である確率を$p$、$X=0$である確率を$1-p$で取り扱うが、多項分布の場合は$(1)$式の$X_{nk}=1$の確率を$p_k$とおき、$p_1, p_2, p_3, \cdots p_{K-1}, p_{K}$のようにそれぞれの値に対する確率を取り扱う。確率パラメータが$p$の二項分布は$\mathrm{Bin}(n,p)$のように表記することが多いが、$N$回の試行に関して確率パラメータが$p_1, p_2, p_3, \cdots p_{K-1}, p_{K}$である多項分布は下記のように表される。
$$
\large
\begin{align}
Y & \sim \mathrm{Multi}(N, p_1, \cdots , p_K) \\
\sum_{k=1}^{K} p_k &= 1
\end{align}
$$
ここで上記の確率関数を$p(y_1,\cdots,y_K)$とおくと$p(y_1,\cdots,y_K)$は$p_1, p_2, p_3, \cdots p_{K-1}, p_{K}$を用いて下記のように表すことができる。
$$
\large
\begin{align}
p(y_1,\cdots,y_K) &= \frac{(y_1 + \cdots + y_K)!}{y_1! \cdots y_K!} p_1^{y_1} \cdots p_K^{y_K} \\
&= \frac{\displaystyle \left( \sum_{k=1}^{K} y_k \right)!}{\displaystyle \prod_{k=1}^{K} y_k!} \prod_{k=1}^{K} p_k^{y_k}
\end{align}
$$
この問題では以下、多項分布の確率関数や期待値、分散、共分散、確率母関数などの表記や導出について取り扱う。下記の問いにそれぞれ答えよ。
i) $n=3, p_1=0.2, p_2=0.5, p_3=0.3$のとき、$y_1=1, y_2=1, y_3=1$である確率を計算せよ。
ⅱ) $1$〜$N$回の試行の$n$回目の試行の確率変数$X_{nk}$に関して期待値$E[X_{nk}]$と分散$V[X_{nk}]$の式をそれぞれ表せ。
ⅲ) 確率変数$Y_k$の期待値$E[Y_{k}]$と分散$V[Y_{k}]$の式をそれぞれ表せ。
iv) 確率変数$X_{nk}, X_{nk’}, \, k \neq k’$の共分散$\mathrm{Cov}(X_{nk}, X_{nk’})$を導出せよ。
v) 確率変数$Y_{k}, Y_{k’}, \, k \neq k’$の共分散$\mathrm{Cov}(Y_{k}, Y_{k’})$を導出せよ。
vi) $X_{n1}, \cdots X_{nK}$に関して確率母関数$G_{X_{n1}, \cdots X_{nK}}(s_1, \cdots, s_K)=E[s_1^{X_{n1}} \cdots s_K^{X_{nK}}]$を定めるとき、$G_{X_{n1}, \cdots X_{nK}}(s_1, \cdots, s_K)$を導出せよ。
vⅱ) vi)を元に確率母関数$G_{Y_{1}, \cdots X_{K}}(s_1, \cdots, s_K)=E[s_1^{Y_{1}} \cdots s_K^{Y_{K}}]$を導出せよ。
・解答
i)
下記のように計算を行うことができる。
$$
\large
\begin{align}
p(y_1,\cdots,y_K) &= \frac{(y_1 + \cdots + y_K)!}{y_1! \cdots y_K!} p_1^{y_1} \cdots p_K^{y_K} \\
&= \frac{(1+1+1)!}{1 \cdot 1 \cdot 1} 0.2^{1} \cdot 0.5^{1} \cdot 0.3^{1} \\
&= 3 \cdot 0.09 = 0.27
\end{align}
$$
ⅱ)
確率変数$X_{nk}$の期待値$E[X_{nk}]$と分散$V[X_{nk}]$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
E[X_{nk}] &= 1 \cdot P(X_{nk}=1) + 0 \cdot P(X_{nk} \neq 1) \\
&= p_{k} \\
E[X_{nk}^{2}] &= 1^2 \cdot P(X_{nk}=1) + 0^2 \cdot P(X_{nk} \neq 1) \\
&= p_{k} \\
V[X_{nk}] &= E[X_{nk}^{2}] – E[X_{nk}]^{2} \\
&= p_{k} – p_{k}^{2} = p_{k}(1-p_{k})
\end{align}
$$
ⅲ)
確率変数$Y_k$の期待値$E[Y_{k}]$と分散$V[Y_{k}]$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
E[Y_{k}] &= E \left[ \sum_{n=1}^{N} X_{nk} \right] \\
&= \sum_{n=1}^{N} E[X_{nk}] \\
&= N p_{k} \\
V[Y_{k}] &= V \left[ \sum_{n=1}^{N} X_{nk} \right] \\
&= \sum_{n=1}^{N} V[X_{nk}] \\
&= N p_{k} (1-p_k)
\end{align}
$$
iv)
共分散$\mathrm{Cov}(X_{nk}, X_{nk’})$は下記のように考えることができる。
$$
\large
\begin{align}
\mathrm{Cov}(X_{nk}, X_{nk’}) &= E[X_{nk} X_{nk’}] – E[X_{nk}] E[X_{nk’}] \\
&= 0 – p_{k} p_{k’} \\
&= – p_{k} p_{k’}
\end{align}
$$
v)
確率変数$Y_{k}, Y_{k’}, \, k \neq k’$の共分散$\mathrm{Cov}(Y_{k}, Y_{k’})$は下記のように表せる。
$$
\large
\begin{align}
\mathrm{Cov}(Y_{k}, Y_{k’}) &= N \mathrm{Cov}(X_{nk}, X_{nk’}) \\
&= – N p_{k} p_{k’}
\end{align}
$$
vi)
確率母関数$G_{X_{n1}, \cdots X_{nK}}(s_1, \cdots, s_K)$は下記のように表せる。
$$
\large
\begin{align}
G_{X_{n1}, \cdots X_{nK}}(s_1, \cdots, s_K) &= E[s_1^{X_{n1}} \cdots s_K^{X_{nK}}] \\
&= p_{1} s_1^{1} \cdots s_K^{0} + \cdots + p_{K} s_1^{0} \cdots s_K^{1} \\
&= p_{1} s_1 + \cdots p_{K} s_{K}
\end{align}
$$
vⅱ)
確率母関数$G_{Y_{1}, \cdots X_{K}}(s_1, \cdots, s_K)=E[s_1^{Y_{1}} \cdots s_K^{Y_{K}}]$は下記のように導出できる。
$$
\large
\begin{align}
G_{Y_{1}, \cdots X_{K}}(s_1, \cdots, s_K) &= E[s_1^{Y_{1}} \cdots s_K^{Y_{K}}] \\
&= E[s_1^{\sum_{n=1}^{N} X_{n1}} \cdots s_K^{\sum_{n=1}^{N} X_{nK}}] \\
&= E \left[ \prod_{n=1}^{N} s_1^{X_{n1}} \cdots \prod_{n=1}^{N} s_1^{X_{n1}} \right] \\
&= \prod_{n=1}^{N} E[s_1^{X_{n1}} \cdots s_K^{X_{nK}}] \\
&= (p_{1} s_1 + \cdots p_{K} s_{K})^{N}
\end{align}
$$
・解説
統計検定準$1$級対応ワークブックの$5$章の内容を元に問題の作成を行いましたので合わせて確認すると良いと思います。
確率変数の定義に関しては下記を参考に作成を行いました。
カテゴリ分布
多項分布
この問題では$X$が従う分布がカテゴリ分布、$Y$が従う分布が多項分布に一致するように確率変数ベクトルの定義を行いました。
連続型確率分布
コーシー分布
・問題
自由度$1$の$t$分布に対応するコーシー分布の確率密度関数を$f(x)$とおくと$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{1}{\pi (1+x^2)}
\end{align}
$$
この問題では以下、コーシー分布の確率密度関数の形状や全区間での積分などに関して演習形式で確認を行う。以下の問いにそれぞれ答えよ。
i) $f(x)$の導関数$f'(x)$を計算し、増減表を作成せよ。
ⅱ) $x=\tan{\theta}$とおき、置換積分を行うことで下記を示せ。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} f(x) dx = \int_{-\infty}^{\infty} \frac{1}{\pi (1+x^2)} dx = 1
\end{align}
$$
ⅲ) 自由度$n$の$t$分布の確率密度関数を$g(x)$とおくと$g(x)$は下記のように表せる。
$$
\large
\begin{align}
g(x) = \frac{\displaystyle \Gamma \left( \frac{n+1}{2} \right)}{\displaystyle \sqrt{\pi n} \Gamma \left( \frac{n}{2} \right)} \left( 1 + \frac{x^2}{n} \right)^{-\frac{n+1}{2}}
\end{align}
$$
上記に$n=1$を代入し、変形を行うとコーシー分布の確率密度関数$f(x)$が得られることを示せ。
・解答
i)
$f'(x)$は下記のように計算できる。
$$
\large
\begin{align}
f'(x) &= ([\pi (1+x^2)]^{-1})’ \\
&= \frac{1}{\pi} \times -\frac{1}{(1+x^2)^2} \times (1+x^2)’ \\
&= -\frac{2x}{\pi (1+x^2)^2}
\end{align}
$$
よって$f(x)$の増減表は下記のように作成できる。
$$
\large
\begin{array}{|c|*5{c|}}\hline x & -\infty & \cdots & 0 & \cdots & \infty \\
\hline f'(x)& & + & 0 & – & \\
\hline f(x)& 0 & \nearrow & \displaystyle \frac{1}{\pi} & \searrow & 0 \\
\hline
\end{array}
$$
ⅱ)
$x=\tan{\theta}$より、$\displaystyle \frac{dx}{d \theta} = \frac{1}{\cos^{2}{\theta}}$である。また、$x$と$\theta$は下記のように対応する。
| $x$ | $-\infty \to \infty$ |
| $\theta$ | $\displaystyle -\frac{\pi}{2} \to \frac{\pi}{2}$ |
よって、下記のように置換積分を行うことができる。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} f(x) dx &= \int_{-\infty}^{\infty} \frac{1}{\pi (1+x^2)} dx \\
&= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{\pi (1+\tan{\theta}^2)} \cdot \frac{1}{\cos^{2}{\theta}} d \theta \\
&= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cancel{\cos^{2}{\theta}}}{\pi} \cdot \frac{1}{\cancel{\cos^{2}{\theta}}} d \theta \\
&= \frac{1}{\pi} \left[ \theta \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
&= \frac{1}{\pi} \left[ \frac{\pi}{2} – \left( -\frac{\pi}{2} \right) \right] \\
&= 1
\end{align}
$$
ⅲ)
$g(x)$に$n=1$を代入すると下記のように変形を行うことができる。
$$
\large
\begin{align}
g(x) &= \frac{\displaystyle \Gamma \left( \frac{1+1}{2} \right)}{\displaystyle \sqrt{\pi \cdot 1} \Gamma \left( \frac{1}{2} \right)} \left( 1 + \frac{x^2}{1} \right)^{-\frac{1+1}{2}} \\
&= \frac{\Gamma(1)}{\displaystyle \sqrt{\pi} \Gamma \left( \frac{1}{2} \right)} (1+x^2)^{-1} \\
&= \frac{1}{\pi(1+x^2)}
\end{align}
$$
・解説
下記などを元に作成を行いました。
対数正規分布
・問題
$Y \sim \mathcal{N}(\mu,\sigma^2)$のように正規分布$\mathcal{N}(\mu,\sigma^2)$に従う確率変数$Y$に関して$X=e^Y$のような変数変換を考えたとき、$X$は対数正規分布$\Lambda(\mu,\sigma^2)$に従う。
対数正規分布$\Lambda(\mu,\sigma^2)$の確率密度関数を$f(x)$とおくと$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{1}{\sqrt{2 \pi \sigma^2} x} \exp{\left( -\frac{(\log{x}-\mu)^2}{2 \sigma^2} \right)}, \quad x>0
\end{align}
$$
以下、上記の確率密度関数の導出や対数正規分布$\Lambda(\mu,\sigma^2)$の$k$次モーメント$E[X^k]$や期待値・分散などの導出に関して演習形式で確認を行う。下記の問いにそれぞれ答えよ。
i) 正規分布$\mathcal{N}(\mu,\sigma^2)$の確率密度関数を$g(y)$とおくとき、$g(y)$を表せ。
ⅱ) i)の$g(y)$に対し、$x=e^{y}$を元に変数変換を行うことで、対数正規分布$\Lambda(\mu,\sigma^2)$の確率密度関数$f(x)$を導出せよ。
ⅲ) $X=e^{Y}$であることを元に、$E[X^{k}]=E[e^{kY}]$であることを確認せよ。
iv) ⅲ)で確認を行った$E[X^{k}]=E[e^{kY}]$より、$E[X^{k}]$は正規分布$\mathcal{N}(\mu,\sigma^2)$のモーメント母関数$m_{Y}(t)=E[e^{tY}]$に$t=k$を代入することで得られる。$m_{Y}(t)$を$\mu, \sigma^2$を用いて表せ。
v) 対数正規分布$\Lambda(\mu,\sigma^2)$の期待値$E[X]$と分散$V[X]$をそれぞれ表せ。
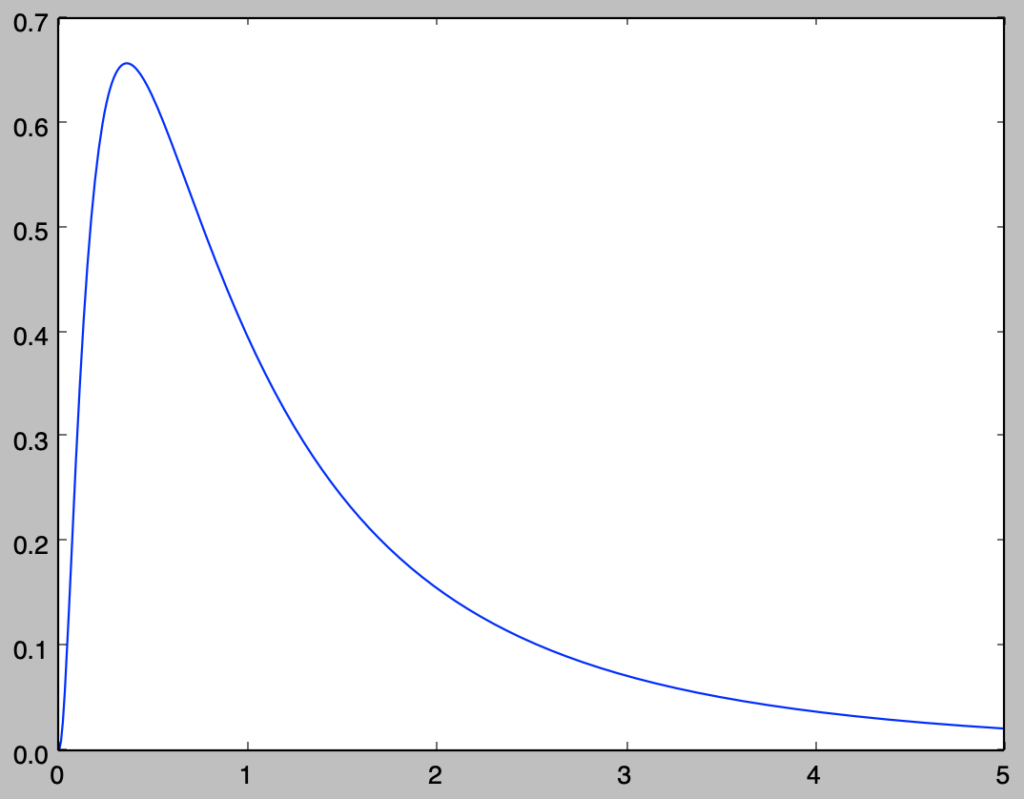
vi) 対数正規分布$\Lambda(0,1^2)$の確率密度関数$f(x)$のグラフを描け。
vⅱ) 対数正規分布$\Lambda(0,1^2)$の確率密度関数$f(x)$に関して下記が成立することを示せ。
$$
\large
\begin{align}
\lim_{x \to +0} f(x) &= 0 \\
\lim_{x \to \infty} f(x) &= 0
\end{align}
$$
・解答
i)
正規分布$\mathcal{N}(\mu,\sigma^2)$の確率密度関数を$g(y)$は下記のように表せる。
$$
\large
\begin{align}
g(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp{\left( -\frac{(y-\mu)^2}{2 \sigma^2} \right)}
\end{align}
$$
ⅱ)
$x=e^{y}$より$y=\log{x}, \, x>0$が得られ、$\displaystyle \frac{dy}{dx} = \frac{1}{x}$である。よって確率密度関数$f(x)$は変数変換の公式を元に下記のように導出できる。
$$
\large
\begin{align}
f(x) &= g(y) \left| \frac{dy}{dx} \right| \\
&= g(\log{x}) \cdot \frac{1}{x} \\
&= \frac{1}{\sqrt{2 \pi \sigma^2} x} \exp{\left( -\frac{(\log{x}-\mu)^2}{2 \sigma^2} \right)}, \quad x>0
\end{align}
$$
ⅲ)
$X=e^{Y}$より、下記のような変形を行える。
$$
\large
\begin{align}
E[X^{k}] &= E[(e^{Y})^{k}] \\
&= E[e^{kY}]
\end{align}
$$
iv)
正規分布$\mathcal{N}(\mu,\sigma^2)$のモーメント母関数$m_{Y}(t)=E[e^{tY}]$は下記のように表せる。
$$
\large
\begin{align}
m_{Y}(t) &= E[e^{tY}] \\
&= \exp{\left( \mu t + \frac{1}{2} \sigma^2 t^2 \right)}
\end{align}
$$
v)
対数正規分布$\Lambda(\mu,\sigma^2)$の期待値$E[X]$と分散$V[X]$はそれぞれ下記のように得られる。
$$
\large
\begin{align}
E[X] &= \exp{\left( \mu \cdot 1 + \frac{1}{2} \sigma^2 \cdot 1^2 \right)} \\
&= \exp{\left( \mu + \frac{1}{2} \sigma^2 \right)} \\
V[X] &= E[X^2] – E[X]^2 \\
&= \exp{\left( \mu \cdot 2 + \frac{1}{2} \sigma^2 \cdot 2^2 \right)} – \exp{\left[ 2 \left( \mu + \frac{1}{2} \sigma^2 \right) \right]} \\
&= \exp{\left( 2 \mu + 2 \sigma^2 \right)} – \exp{\left( 2 \mu + \sigma^2 \right)} \\
&= \exp{(\sigma^2)} \exp{\left( 2 \mu + \sigma^2 \right)} – \exp{\left( 2 \mu + \sigma^2 \right)} \\
&= \exp{\left( 2 \mu + \sigma^2 \right)} (\exp{(\sigma^2)} – 1)
\end{align}
$$
vi)
下記を実行することで対数正規分布$\Lambda(0,1^2)$のグラフを描くことができる。
import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 0., 1.
x = np.arange(0.01, 5.01, 0.01)
f_x = np.e**(-(np.log(x)-mu)**2/(2.*sigma**2))/(np.sqrt(2*np.pi)*sigma*x)
plt.plot(x,f_x)
plt.show()実行結果
vⅱ)
$$
\large
\begin{align}
\lim_{x \to +0} \log{f(x)} &= -\infty \\
\lim_{x \to \infty} \log{f(x)} &= -\infty
\end{align}
$$
$f(x) \to +0 \iff \log{f(x)} \to -\infty$より、上記を示せば良い。
$$
\large
\begin{align}
\lim_{x \to +0} \log{f(x)} &= \log{\left[ \frac{1}{\sqrt{2 \pi} x} \exp{\left( -\frac{(\log{x})^2}{2} \right)} \right]} \\
&= \lim_{x \to +0} \log{f(x)} \left[ -x – \frac{(\log{x})^2}{2} – \frac{1}{2} \log{(2 \pi)} \right] \\
&= -\infty \\
\lim_{x \to \infty} \log{f(x)} &= \lim_{x \to +0} \log{f(x)} \left[ -x – \frac{(\log{x})^2}{2} – \frac{1}{2} \log{(2 \pi)} \right] \\
&= -\infty
\end{align}
$$
よって下記が成立する。
$$
\large
\begin{align}
\lim_{x \to +0} f(x) &= 0 \\
\lim_{x \to \infty} f(x) &= 0
\end{align}
$$
・解説
この問題では対数正規分布$\Lambda(\mu,\sigma^2)$の導出や$k$次モーメント$E[X^k]$や期待値$E[X]$・分散$V[X]$などに関して取り扱いました。統計検定準$1$級のワークブックを元に作成を行いましたが、グラフに関しては解説がないので合わせて抑えておくと良いと思います。
