PointNetは点群(point clouds)の分類(classification)や点単位のセグメンテーション(segmentation)にMLP(Multi Layer Perceptron)を導入した研究です。当記事ではPointNetの論文を元にPointNetの処理手順を取りまとめました。
PointNetの論文である「PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation」や「深層学習 第$2$版」第$7$章の「集合・グラフのためのネットワークと注意機構」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
点群とInvariance
点群は並べ替えに不変であるという特徴を持ちます。同変性を表すequivarenceと不変性を表すinvarianceについては下記で詳しく取り扱ったので当記事では省略します。
点群の取り扱いにあたっては並び替え操作に関する不変性を念頭に置いた上で処理を組む必要があり、PointNetも例外ではないことに注意しておくと良いです。
PointNet
PointNetの処理概要
PointNetの処理の全体像は下図を元に掴むことができます。
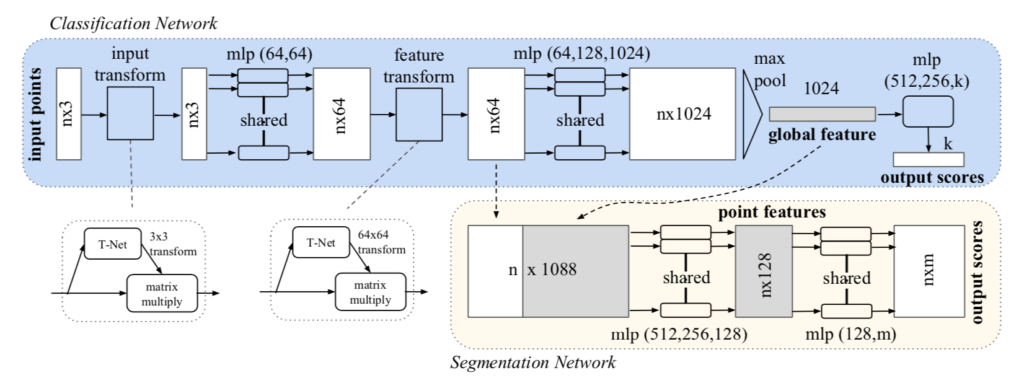
基本的には入力された$n$個の点ごとにMLP(Multi Layer Perceptron)処理を行うことに注意して上図は確認を行うと良いです。図のMLP演算の所に「shared」と記載があるのはMLPの計算に用いるパラメータを共有したと解釈するのが適切だと思われます1。
また、$n \times 1024$にmax poolingを施した結果、$1024$次元の特徴量が得られ、$512$次元$\longrightarrow$$256$次元$\longrightarrow$$k$次元とMLPによって計算され、$k$クラス分類問題に用いられる一連の流れを確認することもできます2。
Max PoolingとInvariance
前節で取り扱ったように点群は並べ替えに対して不変である必要があるので、CNNにおけるダウンサンプリングのように近傍の点と段階的に統合することはできません。したがって、PointNetでは$n \times 1024$の特徴量を点方向にmax poolingすることで大域特徴量(Global Feature)の抽出を行います。
Local and Global Information Aggregation
分類(Classification)タスクを解くにあたってはmax poolingを行うことで得たGlobal Featureをそのまま用いれば良い一方で、セグメンテーション(Segmentation)タスクでは点単位での分類が必要になります。
したがってPointNetでは$n \times 64$の点ごとの特徴量にそれぞれ$1024$次元のGlobal Featureを連結する(concatenate)ことで$n \times 1088$とし、その後の処理を行います。MLPにより、$n \times 1088$は下記のように推移します。
$$
\large
\begin{align}
n \times 1088 & \longrightarrow n \times 512 \longrightarrow n \times 256 \\
& \longrightarrow n \times 128 \longrightarrow n \times 128 \longrightarrow n \times m
\end{align}
$$
上記に基づいて点ごとに$m$クラス分類を行うことで、セグメンテーションを実現することができます。
Joint Alignment Network
点群はrigid transformationのように特定のgeometric transformationsに対して不変(invariant)である必要があります。PointNetではこの対応にあたってアフィン変換を実現する小さなニューラルネットワークであるT-netが導入されます。

[…] 【PointNet論文まとめ】DeepLearningを用いた点群の分類・セグメンテーション […]
[…] 【PointNet論文まとめ】DeepLearningを用いた点群の分類・セグメンテーション […]