当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$2.7.2$節「二項分布」の内容を元に二項分布の確率関数や期待値・分散の計算に関して取りまとめました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
二項分布の概要
概要
二項分布は$X_i=1$の確率が$p$であるベルヌーイ分布に基づくベルヌーイ試行を$n$回行った際に$1$が観測される回数の確率を取り扱います。たとえば確率$p=0.3$で成功する試行を$3$回行った際に$2$度成功する確率$P(X=2|n=3,p=0.3)$は下記のように表すことができます。
$$
\large
\begin{align}
P(X=2|n=3,p=0.3) &= 3 \times 0.3^{2} \times (1-0.3)^{1} \\
&= 0.189
\end{align}
$$
上記では$2$回成功、$1$回失敗を$0.3^{2} \times (1-0.3)^{1}$で表しており、成功が$1$回目・$2$回目・$3$回目のどこで起こるかの$3$通りがあることから$3$を掛けました。一般的な二項分布の確率関数の表記に関しては次節で取り扱います。
必要な数学
ベルヌーイ分布を元に二項分布の期待値や分散の式を表すにあたっては、$\displaystyle \sum$を用いることでシンプルに取り扱えるので抑えておくと良いと思います。
二項分布の確率関数・期待値・分散
二項分布の確率関数
ベルヌーイ分布の確率関数を$p(x)$とおくと、$p(x)$は下記のように表されます。
$$
\large
\begin{align}
p(x) = {}_{n} C_{x} p^{x} (1-p)^{n-x}
\end{align}
$$
式の解釈にあたっては前節で取り扱ったように$x$回成功、$n-x$回失敗を$p^{x} (1-p)^{n-x}$で表し、成功と失敗をどの順序で並べるかを${}_{n} C_{x}$を用いて表したと考えると良いです。
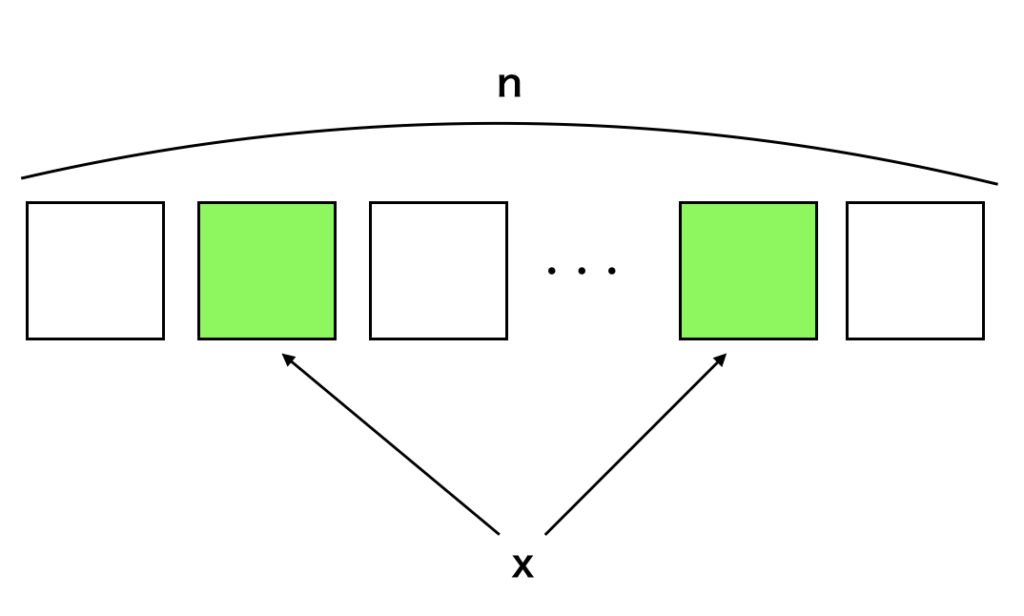
${}_{n} C_{x}$の理解にあたっては上図を元に考えると良いと思います。
二項分布の期待値・分散
二項分布の期待値と分散はベルヌーイ分布を元に計算を行うと良いです。$i$番目のベルヌーイ試行における確率変数を$X_i=1 \mathrm{or} 0$で表すとき、二項分布の確率変数$X$は下記のように定義することができます。
$$
\large
\begin{align}
X = \sum_{i=1}^{n} X_i
\end{align}
$$
「ベルヌーイ分布」より、$E[X_i]=p, V[X_i]=p(1-p)$なので、二項分布の期待値$E[X]$と分散$V[X]$はそれぞれ下記のように考えることができます。
$$
\large
\begin{align}
E[X] &= E \left[ \sum_{i=1}^{n} X_i \right] \\
&= \sum_{i=1}^{n} E[X_i] \\
&= np \\
V[X] &= V \left[ \sum_{i=1}^{n} X_i \right] \\
&= \sum_{i=1}^{n} V[X_i] \\
&= np(1-p)
\end{align}
$$
発展事項
確率変数$X_i$が$0,1$の$2$値を取ることを上記では$X_i=1 \mathrm{or} 0$のように表しましたが、集合の表記を用いて$X_i \in \{ 0,1 \}$と表す場合が多いので抑えておくと良いです。
また、$V[X]$の計算にあたって、$V[X_1+X_2]=V[X_1]+V[X_2]$を用いましたが、$X_1$と$X_2$の相関・共分散が$0$でないとこの式は使えないことに注意が必要です。超幾何分布などが$V[X_1+X_2] \neq V[X_1]+V[X_2]$の例に挙げられますが、下記で詳しく取り扱ったので当項では省略します。
