ブログ

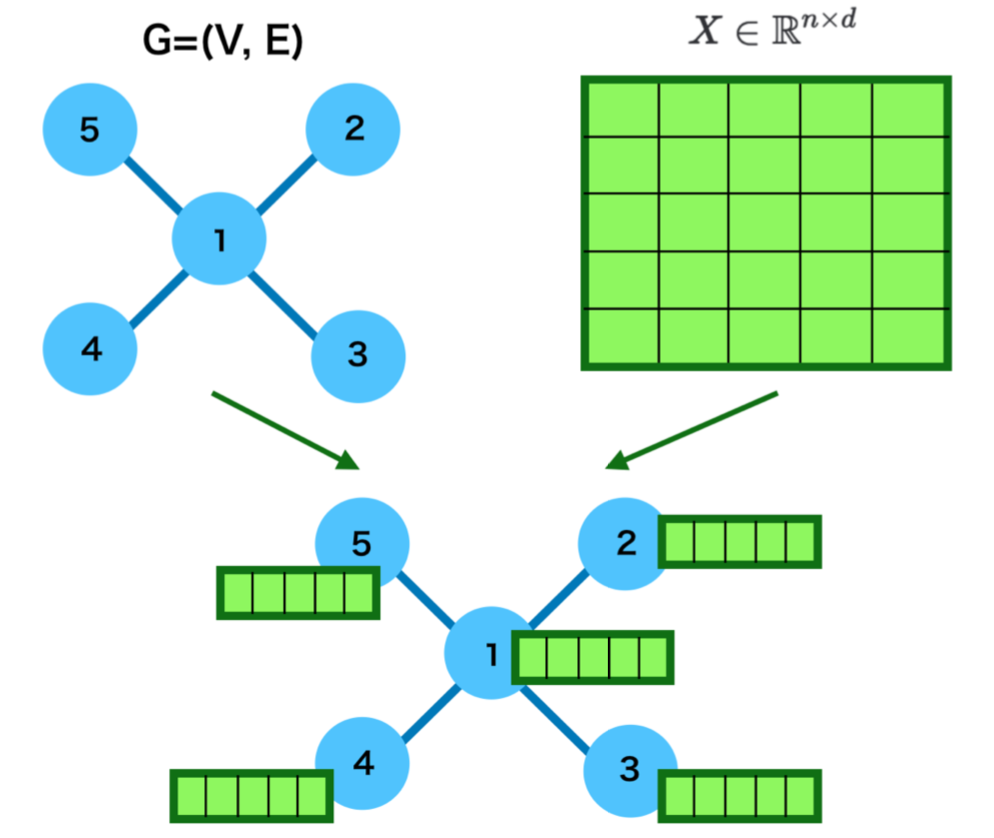
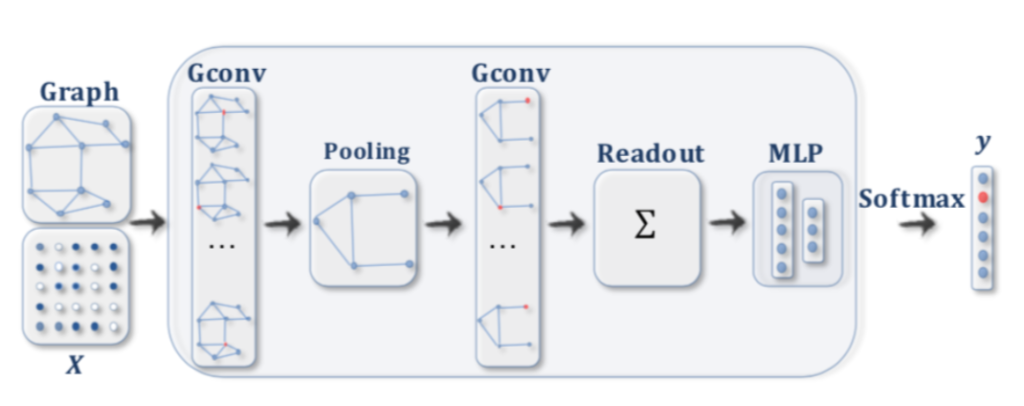
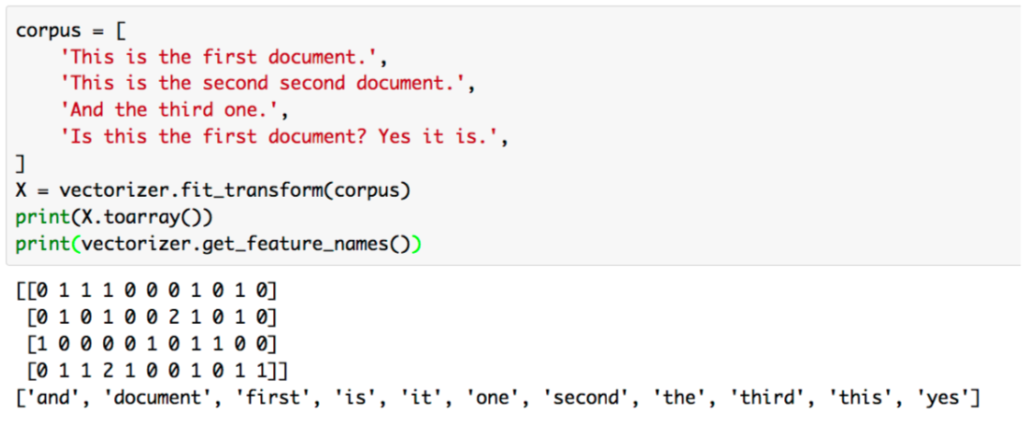
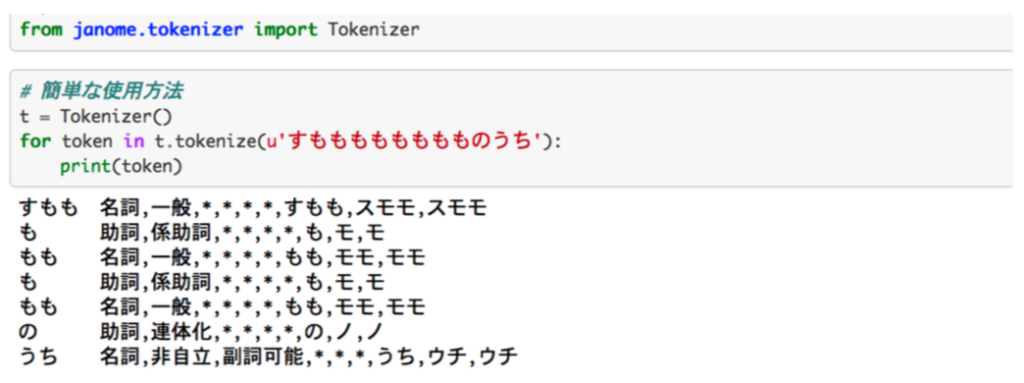
当記事は「言語処理のための機械学習入門(コロナ社)」の読解サポートにあたってChapter.$1$の「必要な数学知識」の章末問題の解説について行います。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

言語処理のための機械学習入門 (自然言語処理シリーズ)

高村 大也

2,399円(11/02 11:32時点)

Amazon

例題解答

例題1.1の解答例

$$
\large
\begin{align}
\mathrm{Objective} : \quad & f(\mathbf{x}) = -x_1x_2 \, \rightarrow \, \mathrm{Maximize} \\
\mathrm{Constraint} : \quad & c_1(\mathbf{x}) = x_1-x_2-a = 0
\end{align}
$$

$x_1-x_2-a = 0$より$x_1=x_2+a$を$f(\mathbf{x}) = -x_1x_2$に代入すると下記が得られる。
$$
\large
\begin{align}
f(\mathbf{x}) &= -x_1x_2 \\
&= -x_2(x_2+a) \\
&= – \left( x_2 + \frac{1}{2}a \right)^{2} + \frac{1}{4}a^2
\end{align}
$$

よって$\displaystyle x_1 = \frac{1}{2}a, x_2=-\frac{1}{2}a$のとき$f(\mathbf{x})$は最大値を取る。

例題1.2の解答例

例題1.3の解答例

$$
\large
\begin{align}
f(x) = -x^2
\end{align}
$$

上記のように定義する$f(x)$に関して$0 \leq t \leq 1$である$t$と、$x_1<x_2$である$x_1,x_2$を用いて下記のような式変形が成立する。
$$
\large
\begin{align}
& f(tx_1 + (1-t)x_2) – \left[ tf(x_1) + (1-t)f(x_2) \right] \\
&= -(tx_1 + (1-t)x_2)^2 – \left[ -tx_1^2 – (1-t)x_2^2 \right] \\
&= -t^2x_1^2 – (1-t)^2x_2^2 – 2t(1-t)x_1x_2 + tx_1^2 + (1-t)x_2^2 \\
&= t(1-t)x_1^2 + (1-t)(1-(1-t))x_2^2 – 2t(1-t)x_1x_2 \\
&= t(1-t)x_1^2 + t(1-t)x_2^2 – 2t(1-t)x_1x_2 \\
&= t(1-t)(x_1^2 + x_2^2 – 2x_1x_2) \\
&= t(1-t)(x_1-x_2)^2 \geq 0
\end{align}
$$

上記より、$f(tx_1 + (1-t)x_2) \geq tf(x_1) + (1-t)f(x_2)$が成立するので$f(x)=-x^2$は上に凸の関数である。

例題1.4の解答例

例題1.5の解答例

例題1.6の解答例

例題1.7の解答例

$$
\large
\begin{align}
\mathrm{Objective} : \quad & f(\mathbf{x}) = -(x_1^2+x_2^2) \, \rightarrow \, \mathrm{Maximize} \\
\mathrm{Constraint} : \quad & c_1(\mathbf{x}) = x_1+x_2-1 = 0
\end{align}
$$

上記の制約付き最適化問題のラグランジュ関数を$L(x_1,x_2,\lambda)$とおくと、$L(x_1,x_2,\lambda)$は下記のように表せる。
$$
\large
\begin{align}
L(x_1,x_2,\lambda) &= f(\mathbf{x}) + \lambda c_1(\mathbf{x}) \\
&= -(x_1^2+x_2^2) + \lambda(x_1+x_2-1)
\end{align}
$$

ここでKKT条件より下記が得られる。
$$
\large
\begin{align}
\frac{\partial L}{\partial x_1} &= -2x_1+\lambda = 0 \quad (1) \\
\frac{\partial L}{\partial x_2} &= -2x_2+\lambda = 0 \quad (2) \\
\frac{\partial L}{\partial \lambda} &= x_1+x_2-1 = 0 \quad (3)
\end{align}
$$

$(1),(2)$式より$x_1=x_2$が得られるので、$(3)$式に代入して最適解$\displaystyle (x_1,x_2) = \left( \frac{1}{2},\frac{1}{2} \right)$が得られる。

・考察
目的関数の等高線や制約条件の直線、最適解における勾配ベクトル$\nabla f(\mathbf{x})$と$\lambda \nabla c_1(\mathbf{x})$の釣り合いは下記を実行することでそれぞれ確認することができる。

import numpy as np
import matplotlib.pyplot as plt

x_, y_ = np.arange(-2., 2.01, 0.01), np.arange(-1., 3.01, 0.01)
x, y = np.meshgrid(x_,y_)
z = -(x**2 + y**2)

levs = np.arange(-3.5,-0., 0.5)

plt.scatter(1/2., 1/2., marker="*", s=300, color="blue")
plt.quiver(1/2., 1/2., 1, 1, color="red", angles='xy', scale_units='xy', scale=1)
plt.quiver(1/2., 1/2., -1, -1, color="green", angles='xy', scale_units='xy', scale=1)

plt.plot(x_, -x_+1, "r--")
plt.contour(x,y,z,levels=levs,cmap="viridis")

plt.colorbar()
plt.show()

実行結果

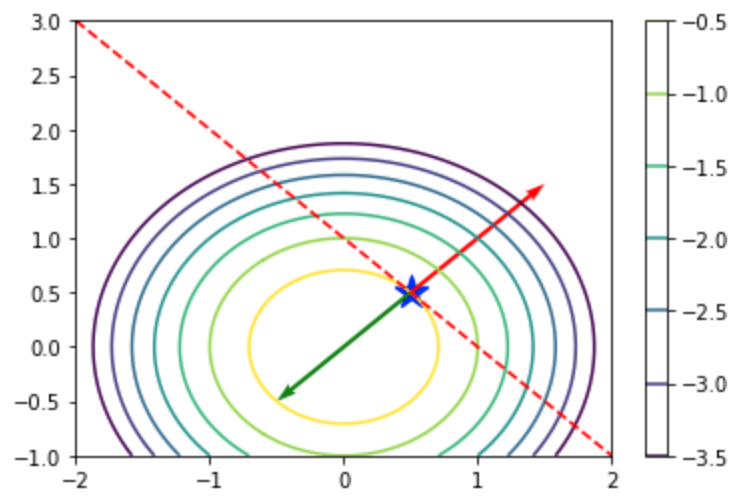
例題1.8の解答例

例題1.9の解答例

例題1.10の解答例

$X^2$の期待値を$E[X^2]$とおくと、$E[X]$は下記のように計算できる。
$$
\large
\begin{align}
E[X^2] &= \sum_{k=1}^{6} k^2 P(X=k) \\
&= \frac{1}{6} \sum_{k=1}^{6} k^2 \\
&= \frac{1}{6} \times \frac{1}{6} \cdot 6 \cdot (6+1) \cdot (12+1) \\
&= \frac{91}{6} \\
& \simeq 15.17
\end{align}
$$

例題1.11の解答例

例題1.12の解答例

標本平均を$\bar{x}$とおくと、標本平均の定義に基づいて下記のように計算を行うことができる。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{8} \sum_{i=1}^{8} x_i \\
&= \frac{1}{8} (3+6+5+5+2+4+5+2) \\
&= 4
\end{align}
$$

例題1.13の解答例

例題1.14の解答例

条件付き確率の定義に基づいて下記が成立する。
$$
\large
\begin{align}
P(x,y) &= P(y|x)P(x) \quad (1) \\
P(x,y) &= P(x|y)P(y) \quad (2)
\end{align}
$$

$(1),(2)$式より下記が成立する。
$$
\large
\begin{align}
P(y|x)P(x) &= P(x|y)P(y) \\
P(y|x) &= \frac{P(x|y)P(y)}{P(x)}
\end{align}
$$

例題1.15の解答例

$P(x_1,x_2,x_3)$は条件付き確率の定義式を元に下記のように表すことができる。
$$
\large
\begin{align}
P(x_1,x_2,x_3) &= P(x_1|x_2,x_3)P(x_2,x_3) \\
&= P(x_1|x_2,x_3)P(x_2|x_3)P(x_3) \quad (1)
\end{align}
$$

また、下記のようにも表すことができる。
$$
\large
\begin{align}
P(x_1,x_2,x_3) &= P(x_2|x_1,x_3)P(x_1,x_3) \\
&= P(x_2|x_1,x_3)P(x_1|x_3)P(x_3) \quad (2)
\end{align}
$$

$(1), (2)$式より下記が成立する。
$$
\large
\begin{align}
P(x_2|x_1,x_3)P(x_1|x_3) \cancel{P(x_3)} &= P(x_1|x_2,x_3)P(x_2|x_3) \cancel{P(x_3)} \\
P(x_2|x_1,x_3)P(x_1|x_3) &= P(x_1|x_2,x_3)P(x_2|x_3) \\
P(x_2|x_1,x_3) &= \frac{P(x_2|x_3)P(x_1|x_2,x_3)}{P(x_1|x_3)}
\end{align}
$$

例題1.16の解答例

$E[X]$は下記のように計算できる。
$$
\large
\begin{align}
E[X] &= 1 \cdot p + 0 \cdot (1-p) \\
&= p
\end{align}
$$

例題1.17の解答例

$X \sim \mathrm{Bin}(5,0.8)$である確率変数$X$に対し、下記のように$P(X=3)$を計算すれば良い。
$$
\large
\begin{align}
P(X=3) &= {}_{5} C_{3} \cdot 0.8^{3} \cdot 0.2^{2} \\
&= 10 \cdot 0.8^{3} \cdot 0.2^{2} \\
&= 0.2048
\end{align}
$$

例題1.18の解答例

観測値を$\mathbf{x}=(x_1,\cdots,x_6)$、$P$氏の確率を$P(\mathbf{x}|P)$、$N$氏の確率を$P(\mathbf{x}|N)$とおく。このとき$P(\mathbf{x}|P)$と$P(\mathbf{x}|N)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
P(\mathbf{x}|P) &= \frac{6!}{2!1!1!2!} 0.4^{2} 0.1^{1} 0.3^{1} 0.2^{2} = 0.03456 \\
P(\mathbf{x}|N) &= \frac{6!}{2!1!1!2!} 0.1^{2} 0.4^{1} 0.2^{1} 0.3^{2} = 0.01296
\end{align}
$$

例題1.19の解答例

パラメータ$\mu$に関する尤度を$L(\mu)$とおくと、$L(\mu)$は下記のように得られる。
$$
\large
\begin{align}
L(\mu) &= P(D|\mu) \\
&= \prod_{i=1}^{N} \frac{\mu^{x^{(i)} e^{-\mu}}}{x^{(i)}!}
\end{align}
$$

上記に対し、対数尤度$\log{L(\mu)}$は下記のように得られる。
$$
\large
\begin{align}
\log{L(\mu)} &= \log{\left[ \prod_{i=1}^{N} \frac{\mu^{x^{(i)}} e^{-\mu}}{x^{(i)}!} \right]} \\
&= \sum_{i=1}^{N} \log{\left[ \frac{\mu^{x^{(i)}} e^{-\mu}}{x^{(i)}!} \right]} \\
&= \sum_{i=1}^{N} (x^{(i)}\log{\mu} – \mu -\log{x^{(i)}!})
\end{align}
$$

上記の$\mu$に関する微分は標本平均$\bar{x}$を用いて下記のように表せる。
$$
\large
\begin{align}
\frac{\partial \log{L(\mu)}}{\partial \mu} &= \sum_{i=1}^{N} \left[ \frac{x^{(i)}}{\mu} – 1 \right] \\
&= \frac{N \bar{x}}{\mu} – N \\
&= \frac{N(\bar{x}-\mu)}{\mu}
\end{align}
$$

上記より、対数尤度$\log{L(\mu)}$と尤度$L(\mu)$を最大にする$\mu$は$\mu=\bar{x}$であることが得られる。

例題1.20の解答例

$N=n_{\mathrm{good}}+n_{\mathrm{bad}}+n_{\mathrm{exciting}}+n_{\mathrm{boring}}=10$であるので、それぞれ下記が成立する。
$$
\large
\begin{align}
p_{\mathrm{good}} &= \frac{n_{\mathrm{good}}}{N} \\
&= \frac{5}{10} = 0.5 \\
p_{\mathrm{bad}} &= \frac{n_{\mathrm{bad}}}{N} \\
&= \frac{1}{10} = 0.1 \\
p_{\mathrm{exciting}} &= \frac{n_{\mathrm{exciting}}}{N} \\
&= \frac{4}{10} = 0.4 \\
p_{\mathrm{boring}} &= \frac{n_{\mathrm{boring}}}{N} \\
&= \frac{0}{10} = 0
\end{align}
$$

例題1.21の解答例

“Yes”の発言回数を確率変数$X$で表すと、$X \sim \mathrm{Bin}(5,p)$が成立する。このとき尤度$L(p)=P(X_1=2,X_2=3,X_3=3)$は下記のように表せる。
$$
\large
\begin{align}
L(p) &= P(X_1=2, X_2=3, X_3=3) \\
&= P(X_1=2)P(X_2=3)P(X_3=3) \\
&= {}_{5} C_{2} ({}_{5} C_{3})^{2} p^{8} (1-p)^{7}
\end{align}
$$

上記に対し、対数尤度$\log{L(p)}$は下記のように得られる。
$$
\large
\begin{align}
\log{L(p)} = 8 \log{p} + 7 \log{(1-p)}
\end{align}
$$

上記の$p$に関する微分は下記のように得られる。
$$
\large
\begin{align}
\frac{\partial \log{L(p)}}{\partial p} &= \frac{8}{p} – \frac{7}{1-p} \\
&= \frac{8(1-p)-7p}{p(1-p)} \\
&= \frac{8-15p}{p(1-p)}
\end{align}
$$

上記より最尤推定解は$\displaystyle p=\frac{8}{15}$である。

例題1.22の解答例

例題1.23の解答例

$P_{\mathrm{Bin}}(X=0), P_{\mathrm{Bin}}(X=1), P_{\mathrm{Bin}}(X=2), P_{\mathrm{Bin}}(X=3)$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
P_{\mathrm{Bin}}(X=0) &= {}_{3} C_{0} \times 0.8^0 \times 0.2^3 = 0.2^3 \\
P_{\mathrm{Bin}}(X=1) &= {}_{3} C_{1} \times 0.8^1 \times 0.2^2 = 3 \times 0.8 \times 0.2^2 \\
P_{\mathrm{Bin}}(X=2) &= {}_{3} C_{2} \times 0.8^2 \times 0.2^1 = 3 \times 0.8^2 \times 0.2 \\
P_{\mathrm{Bin}}(X=3) &= {}_{3} C_{3} \times 0.8^3 \times 0.2^0 = 0.8^3
\end{align}
$$

上記を元にエントロピーの定義より$H(P_{\mathrm{Bin}})$は下記のように計算できる。
$$
\large
\begin{align}
H(P_{\mathrm{Bin}}) &= -\sum_{k=0}^{3} P_{\mathrm{Bin}}(X=k) \log{P_{\mathrm{Bin}}(X=k)} \\
&= -0.2^3 \log{0.2^3} – (3 \times 0.8 \times 0.2^2) \log{(3 \times 0.8 \times 0.2^2)} – (3 \times 0.8^2 \times 0.2) \log{(3 \times 0.8^2 \times 0.2)} – 0.8^3 \log{0.8^3} \\
&=
\end{align}
$$

例題1.24の解答例

例題1.25の解答例

演習問題解答

問題1.1の解答例

問題1.2の解答例

問題1.3の解答例

問題1.4の解答例

問題1.5の解答例

問題1.6の解答例

問題1.7の解答例

問題1.8の解答例

期待値を$E[X]$とおくと$E[X]$は下記のように計算できる。
$$
\large
\begin{align}
E[X] &= \frac{1}{6}(1+2+3+4+5+6) \\
&= \frac{21}{6} \\
&= \frac{7}{2}
\end{align}
$$

問題1.9の解答例

$P(x_1,x_2,x_3,x_4)$は条件付き確率の定義に基づいて下記のように表せる。
$$
\large
\begin{align}
P(x_1,x_2,x_3,x_4) = P(x_1,x_2|x_3,x_4)P(x_3,x_4) \quad (1)
\end{align}
$$

同様に条件付き確率の定義を用いることで下記のように表すこともできる。
$$
\large
\begin{align}
P(x_1,x_2,x_3,x_4) &= P(x_1|x_2,x_3,x_4)P(x_2,x_3,x_4) \\
&= P(x_1|x_2,x_3,x_4)P(x_2|x_3,x_4)P(x_3,x_4) \quad (2)
\end{align}
$$

$(1), (2)$式より下記が成立する。
$$
\large
\begin{align}
P(x_1,x_2|x_3,x_4) \cancel{P(x_3,x_4)} &= P(x_1|x_2,x_3,x_4) P(x_2|x_3,x_4) \cancel{P(x_3,x_4)} \\
P(x_1,x_2|x_3,x_4) &= P(x_1|x_2,x_3,x_4) P(x_2|x_3,x_4)
\end{align}
$$

上記より与式が示される。

問題1.10の解答例

$X \sim \mathrm{Bin}(5,0.8)$である確率変数$X$に対し、下記のように$P(X=3)+P(X=4)+P(X=5)$を計算すれば良い。
$$
\begin{align}
P(X=3) + P(X=4) + P(X=5) &= {}_{5} C_{3} \cdot 0.8^{3} \cdot 0.2^{2} + {}_{5} C_{4} \cdot 0.8^{4} \cdot 0.2^{1} + {}_{5} C_{5} \cdot 0.8^{5} \cdot 0.2^{0} \\
&= 10 \cdot 0.8^{3} \cdot 0.2^{2} + 5 \cdot 0.8^{4} \cdot 0.2^{1} + 0.8^{5} \cdot 0.2^{0} \\
&= 0.942 \cdots
\end{align}
$$

問題1.11の解答例

問題1.12の解答例

問題1.13の解答例

問題1.14の解答例

問題1.15の解答例

問題1.16の解答例

問題1.17の解答例

まとめ