数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事ではノンパラメトリック法の理解にあたって、順位和検定、並べ替え検定、符号検定などのPythonでの実装を取り扱いました。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
ノンパラメトリック法まとめ
Pythonを用いた処理
順位和検定
順位和検定は、2つの群$A,B$に関してそれぞれ観測値が得られるとき、観測値を小さい順に並べ、$A$の順位和の$P$値を計算する手法である。計算にあたっては組み合わせの計算を主に行う。処理の一連の流れは下記のようにPythonを用いて表すことができる。
・順位和の計算
import numpy as np
x = np.array([5., 10., 15., 12., 16., 20.])
x_A = x[:3]
x_B = x[3:]
rank_A, rank_B = np.argsort(x)[:3]+1, np.argsort(x)[3:]+1
sum_rank_A, sum_rank_B = np.sum(rank_A), np.sum(rank_B)
print("(x_A, x_B): ({}, {})".format(x_A, x_B))
print("(rank_A, rank_B): ({}, {})".format(rank_A, rank_B))
print("(sum_rank_A, sum_rank_B): ({}, {})".format(sum_rank_A, sum_rank_B))・実行結果
> print("(x_A, x_B): ({}, {})".format(x_A, x_B))
(x_A, x_B): ([ 5. 10. 15.], [ 12. 16. 20.])
> print("(rank_A, rank_B): ({}, {})".format(rank_A, rank_B))
(rank_A, rank_B): ([1 2 4], [3 5 6])
> print("(sum_rank_A, sum_rank_B): ({}, {})".format(sum_rank_A, sum_rank_B))
(sum_rank_A, sum_rank_B): (7, 14)・$P$値の計算
x = np.array([5., 10., 15., 12., 16., 20.])
x_A = x[:3]
x_B = x[3:]
rank_x = np.argsort(x)+1
rank_A, rank_B = rank_x[:3], rank_x[3:]
sum_rank_A, sum_rank_B = np.sum(rank_A), np.sum(rank_B)
count_A, count_all = 0., 0.
for i in range(x.shape[0]-2):
for j in range(i+1,x.shape[0]-1):
for k in range(j+1,x.shape[0]):
count_all += 1.
if (rank_x[i]+rank_x[j]+rank_x[k]) <= sum_rank_A:
count_A += 1.
print("P-value: {}/{}={}".format(int(count_A), int(count_all), count_A/count_all))・実行結果
> print("P-value: {}/{}={}".format(int(count_A), int(count_all), count_A/count_all))
P-value: 2/20=0.1並べ替え検定
下記で取り扱いを行った。
https://www.hello-statisticians.com/explain-books-cat/stat_workbook/stat_workbook_ch13.html#132
符号付き順位検定
符号検定
符号検定(sign test)は$n$個の観測値に関して値が正の観測値の数を$T_{+}$のように数え、この個数が二項分布$Bin(n,0.5)$に従うことに基づいて行う検定である。以下、$n=10$の場合で考える。
・二項分布$Bin(10,0.5)$の描画
import math
import numpy as np
import matplotlib.pyplot as plt
def calc_combination_vec(n, vec):
res = np.zeros(11)
for i in range(vec.shape[0]):
res[i] = math.factorial(n) / (math.factorial(vec[i]) * math.factorial(n-vec[i]))
return res
x = np.arange(0.,11.,1.)
p = calc_combination_vec(10, x) * 0.5**10
plt.bar(x, p, color="lightblue")
plt.show()・実行結果
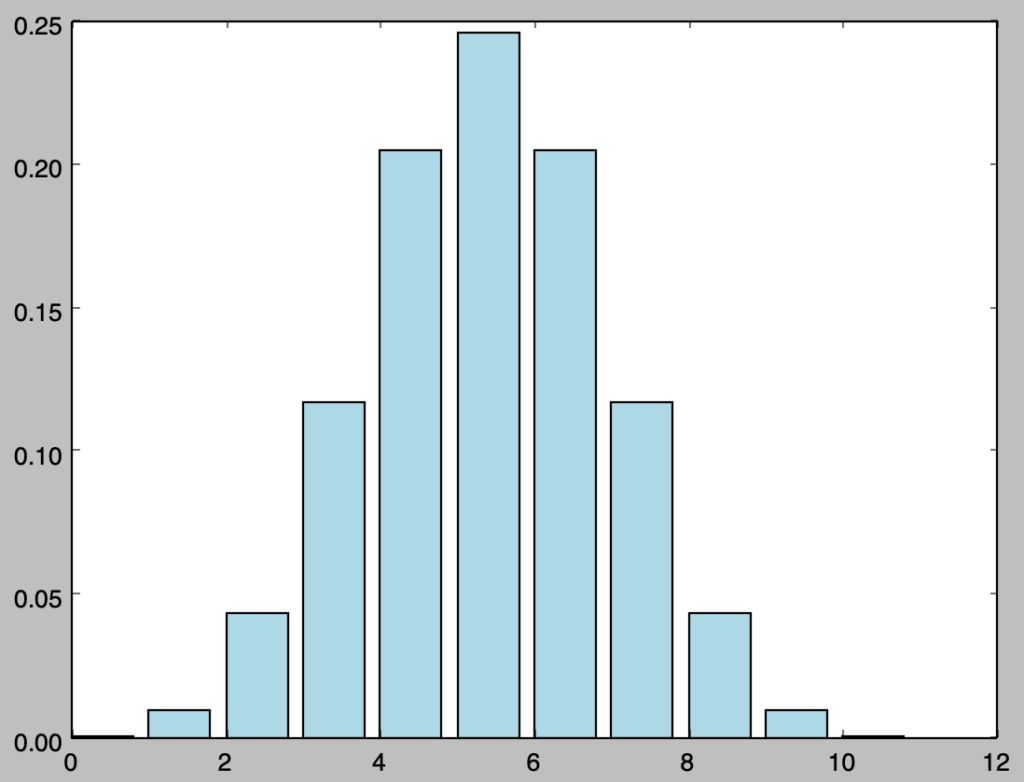
・$P$値の計算
x = np.arange(0.,11.,1.)
T = np.array([8., 9., 10.])
p = calc_combination_vec(10, x) * 0.5**10
p_value = np.array([np.sum(p[8:]), np.sum(p[9:]), np.sum(p[10:])])
print("P_value: {}".format(p_value))・実行結果
> print("P_value: {}".format(p_value))
P_value: [ 0.0546875 0.01074219 0.00097656]クラスカル・ウォリス検定
下記で取り扱いを行った。
https://www.hello-statisticians.com/explain-books-cat/stat_workbook/stat_workbook_ch13.html#134
