当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$29$の「重積分での変数変換」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。
・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook_math#math_stat
本章のまとめ
演習問題解答
問題$29.1$
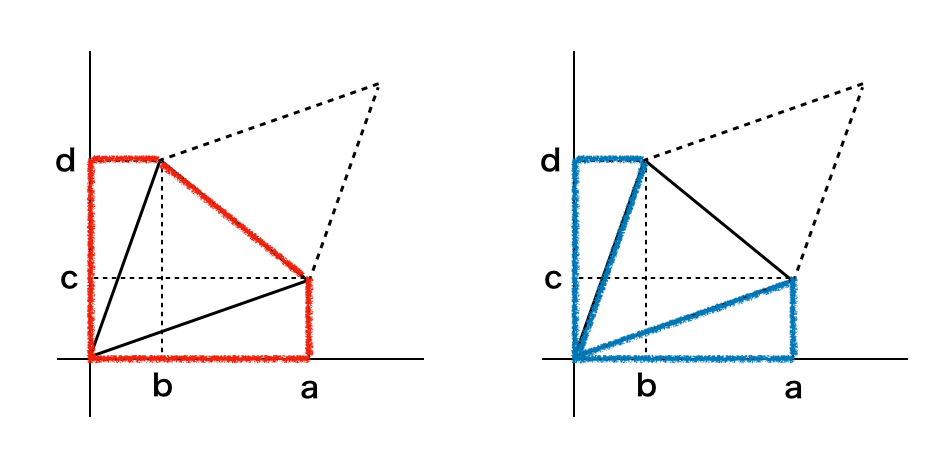
上記の図の「左の赤で囲った面積」から「右の青で囲った面積」を引いた面積を$S$とおくと、平行四辺形の面積は$2S$で計算できる。$2S = ad – bc$が成立することを以下に示す。
$$
\large
\begin{align}
2S &= 2 \times \left[ \left( ac + \frac{1}{2}(a+b)(d-c) \right) – \left( \frac{1}{2}ac + \frac{1}{2}bd \right) \right] \\
&= 2ac+(a+b)(d-c) – (ac+bd) \\
&= \cancel{2ac} + ad – \cancel{ac} + \cancel{bd} – bc – \cancel{ac} – \cancel{bd} = ad – bc
\end{align}
$$
・別解
下記のように内積の式や三角関数の加法定理を用いて導出を行なっても良い。
問題$29.2$
$$
\large
\begin{align}
\int \int_{D} \frac{1}{\sqrt{a^2-(x^2+y^2)}} \, dxdy, \quad D=\{ (x,y) | x^2+y^2 \leq a^2 \}, \quad a > 0
\end{align}
$$
上記に対し、$x = r \cos{\theta}, y = r \sin{\theta}$のような変数変換を考える。このとき変数変換にあたってのヤコビ行列式を$\det{J}$とおくと$\det{J}$は下記のように計算できる。
$$
\large
\begin{align}
\det{J} &= \left| \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right| \\
&= \left| \begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right| \\
&= r(\cos^{2}{\theta} + \sin^{2}{\theta}) = r
\end{align}
$$
また、$x^2+y^2 \leq a^2$に対応する$r, \theta$の範囲は下記のように表せる。
| $r$ | $0 \to a$ |
| $\theta$ | $0 \to 2 \pi$ |
よって重積分は下記のように計算できる。
$$
\large
\begin{align}
& \int \int_{D} \frac{1}{\sqrt{a^2-(x^2+y^2)}} \, dxdy, \quad D=\{ (x,y) | x^2+y^2 \leq a^2 \}, \quad a > 0 \\
&= \int \int_{D’} \frac{1}{\sqrt{a^2-r^2}} \det{J} \, dr d \theta, \quad D’=\{ (r,\theta) | 0 \leq r \leq a, 0 \leq \theta \leq 2 \pi \} \\
&= \int_{0}^{2 \pi} 1 d \theta \times \int_{0}^{a} \frac{r}{\sqrt{a^2-r^2}} dr \\
&= \int_{0}^{2 \pi} 1 d \theta \times \int_{0}^{a} \left( -\sqrt{a^2-r^2} \right)’ dr \\
&= \left[ \theta \right]_{0}^{2 \pi} \times \left[ -\sqrt{a^2-r^2} \right]_{0}^{a} \\
&= 2 \pi \times a \\
&= 2 \pi a
\end{align}
$$
