統計検定準1級対応の公式テキストである「統計学実践ワークブック」を1章から順に演習問題を中心に解説していきます。
今回は第1章「事象と確率」です。
重要ポイント
第1章で抑えておくべきポイントは、条件付き確率(conditional probability)、確率関数(probability function)、期待値(expectation)です。
条件付き確率とベイズの定理
2つの事象A, Bがあり、事象Aの生じる確率を$p(A)$と表現します。また、AとBが同時に生じる確率を$p(A \cap B)$と表します。このあたりはベン図を思い浮かべると理解しやすいですね(下図)。
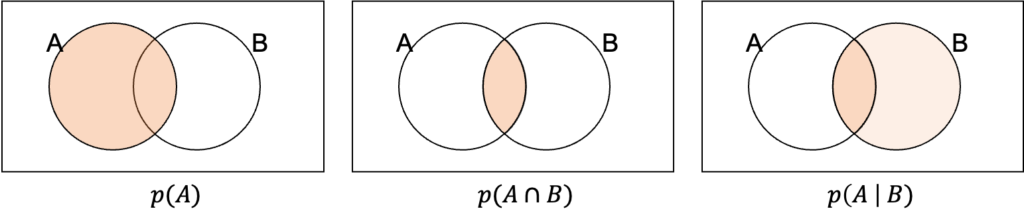
上図の右端である$p(A|B)$を条件付き確率と呼びます。これは、事象Bが生じたという条件の下でのAの生じる確率です。図から想像できますが、$p(A \cap B)$と以下の関係が成り立ちます。
$$
p(A | B) = \frac{p(A \cap B)}{p(A)}
$$
この関係は対称性があり、変形させると条件付き確率は以下のような関係があることがわかります。
$$
\begin{eqnarray}
p(A \cap B) = p(A | B)p(B) &= p(B | A)p(A) \\\
p(A | B) &= \frac{p(B | A)p(A)}{p(B)}
\end{eqnarray}
$$
この関係は特に、「ベイズの定理」と呼ばれています。特別な名前がついていますが、特に気にする必要はありません。条件付き確率の性質を使えば自然に導かれる式です。
確率関数
確率を考える対象であるランダムに変動する変数のことを「確率変数(random variable)」と呼びます。この確率変数(X)が実際に取りうる値(x)についての関数を確率関数(probability function) $p(x)$と呼びます。
この確率関数ですが、Xが連続値を取る場合は特に、確率密度関数(probability density function)と呼ばれています。確率なので、Xの取りうる全ての範囲を合わせると1になります。
$$
\int p(x) dx = 1.0
$$
Xが離散値(コインの裏表やサイコロの目など)を取る場合には、確率質量関数(probability mass function)と呼ばれています。これも確率の定義通り、全ての事象について足し合わせると1になります。(xが離散の値なので、積分ではなく総和になっています)
$$
\sum p(x) = 1.0
$$
期待値
確率変数Xの期待値$E[X]$は平均値とも呼ばれています。
以下の式で定義されており、とりうる全てのXに対して確率$p(x)$をかけて足し合わせたものです。
$$
E[X] = \sum_x xp(x)
$$
Xが連続型の確率変数の場合には、積分になります。
$$
E[X] = \int xp(x) dx
$$
期待値については、合わせてこちらも参照ください。
演習問題解説
演習問題の全文は掲載しません。テキストは各自で用意するか、以下の抜粋から想像してください。
問題概要 [1.1]
ある試験を受験した女性の比率が0.4で、男性合格率は0.4、女性比率は0.5だった。

(1) この試験全体の合格率は?
受験者全体の人数を$x$として、合格者の人数を$y$とします。すると男性受験者は$0.6x$、女性受験者は$0.4x$と表現できます。次に、合格者の人数$y$をxを使って表現すると以下の通りとなります。
$$
y = 0.6 x \cdot 0.4 + 0.4x \cdot 0.5
$$
「合格率」は単純に$y/x$ですので、$x, y$それぞれの関係から以下のように導出できます。
$$
\mathrm{rate} = \frac{y}{x} = (0.6 \cdot 0.4 + 0.4 \cdot 0.5) = 0.44
$$
(2) この試験の合格者の中から、ランダムに選んだ一人が女性である確率は?
この問題は、ベイズの定理を使っても計算できますが、以下のように考えた方が簡単だと思います。ベイズの定理を使った回答例はテキストを参照してください。
ランダムに選んだ一人が女性の確率とは、結局、合格者の中での女性比率ということになります。男性、女性それぞれの合格者の人数をxを使って表現すると以下のようになります。((1)の回答参照)
$$
\begin{eqnarray}
男性 = 0.24 x \\
女性 = 0.2 x
\end{eqnarray}
$$
女性の比率を算出します。
$$
$$
\begin{eqnarray}
\frac{0.2x}{0.24x + 0.2x} = \frac{0.2}{0.44} = \frac{5}{11}
\end{eqnarray}
問題概要 [1.2 ]
1,2,3の3種類の数字”だけ”が書かれているサイコロがあります。それぞれの数字がいくつ書かれているかは不明だが、少なくとも1回は書かれているものとします。
このサイコロで、1が出る確率と2が出る確率は等しい。また、各面が出る確率は$1/6$だとします。
このサイコロの期待値は2より大きいということがわかっているとします。
(1) このサイコロの期待値と分散は?
$p(X=1) = p(X=2)$ということなので、サイコロの目のパターンは二通りが考えられます。1~3の数字が2回づつ書かれているパターンと1と2は1回で3だけ4回書かれているパターンです。どっちかはわからないので、両パターンの期待値を計算してみます。
【2回づつのパターン】
$p(x)=\frac{1}{3}$となるので、以下のように計算できます。
$$
E[X] = \sum xp(x) = \frac{1}{3}(1+2+3) = 2
$$
問題に期待値は2より大きいとなっているため、この時点でこの2回づつパターンではないことがわかります。
ということで、あとは期待値と分散の定義に従って計算するだけ。
【3が4回書かれているパターン】
数字のパターンから、$p(X=1) = p(X=2) = \frac{1}{6}$で$p(X=3)=\frac{4}{6}$です。
$$
\begin{eqnarray}
E[X] &=& \sum xp(x) = \frac{1}{6}(1+2) + \frac{4}{6}(3) = \frac{5}{2}
\end{eqnarray}
$$
次に分散です。
$$
\begin{eqnarray}
V[X] = E[(x-\bar{x})^2] = E[x^2] – (E[X])^2
\end{eqnarray}
$$
ここで、
$$
E[X^2] = \frac{1}{6}(1^2 + 2^2) + \frac{4}{6}(3^2) = \frac{41}{6}
$$
なので、
$$
V[X] = \frac{41}{6} – \left( \frac{5}{2} \right)^2 = \frac{7}{12}
$$
です。
(2) このサイコロを2回投げて大きい方の数字を確率変数Yとするとき、確率P(Y=3)は?
2回投げて大きい方が3になるということなので、少なくとも1回は3が出る確率を考えます。つまり、3が出ないケースを1から引けば良いです。
$$
\begin{eqnarray}
P(Y=3) &=& 1 – p(X_1 \le 2, X_2 \le 2) \\
&=& 1 – p(X_1 \le 2)p(X_2 \le 2) \\
&=& 1 – \frac{2}{6}\frac{2}{6} = \frac{8}{9}
\end{eqnarray}
$$
問題概要 [1.3]
100人に一人の割合でかかる病気があります。
2段階の検査(検査1、検査2)があり、検査1では真に病気の人を99.0%で陽性と示しますが、病気ではない場合でも2%の確率で陽性になります。検査2は、検査1で陽性の人に対して行われる検査で真に病気の人は90%で陽性になりますが、病気ではなくても10%で陽性を示します。
(1) Aさんが検査1で陽性反応が出た場合に本当に病気の確率はいくらか?
検査で陽性反応が出たことを条件として、真に病気である確率を条件付き確率の性質(ベイズの定理)をそのまま使って算出します。
$$
\begin{eqnarray}
p(病気 | 検査1陽性) = \frac{p(検査1陽性 | 病気)p(病気)}{p(検査1陽性)}
\end{eqnarray}
$$
ここで、分母の$p(検査1陽性)$は以下のように算出します。
$$
\begin{eqnarray}
p(検査1陽性) &=& p(検査1陽性 | 病気)p(病気) + p(検査1陽性 | \bar{病気})p(\bar{病気}) \\
&=& 0.99 \cdot \frac{1}{100} + 0.02 \cdot \frac{99}{100} \\
&=& \frac{2.97}{100}
\end{eqnarray}
$$
ということで確率は以下の通りです。
$$
\begin{eqnarray}
p(病気 | 検査1陽性) &=& \frac{p(検査1陽性 | 病気)p(病気)}{p(検査1陽性)} \\
&=& 0.99 \cdot \frac{1}{100} \cdot \frac{100}{2.97} \\
&=& \frac{1}{3}
\end{eqnarray}
$$
病気の確率はまだまだ全然低いですね。
(2) Aさんが検査2でも陽性反応が出た場合に本当に病気の確率はいくらか?
これも(1)とほとんど同じですが、検査2は「検査1で陽性反応の人が受診する」ということです。 事前分布が検査1と異なり、「検査1で陽性反応の人」となります。
$$
\begin{eqnarray}
p(病気 | 検査2陽性, 検査1陽性) = \frac{p(検査2陽性 | 病気, 検査1陽性) p(病気 | 検査1陽性)}{p(検査2陽性)}
\end{eqnarray}
$$
これからわかる通り、分子の事前分布は(1)で導出した$p(病気 | 検査1陽性)$です。
また、ここでの分母は次のように導出されます。ここも(1)の結果を使います(なんせ、検査2は検査1をパスした人だけが対象ですから)。
$$
\begin{eqnarray}
p(検査2陽性) &=& p(検査2陽性 | 病気, 検査1陽性)p(病気 | 検査1陽性) + p(検査2陽性 | \bar{病気}, 検査1陽性)p(\bar{病気}, 検査1陽性) \\
&=& 0.9 \cdot \frac{1}{3} + 0.1 \cdot \frac{2}{3} \\
&=& \frac{1.1}{3}
\end{eqnarray}
$$
ということで、最終的な病気の確率は以下の通りです。
$$
\begin{eqnarray}
p(病気 | 検査2陽性, 検査1陽性) &=& \frac{p(検査2陽性 | 病気, 検査1陽性) p(病気 | 検査1陽性)}{p(検査2陽性)} \\
&=& 0.9 \cdot \frac{1}{3} \cdot \frac{3}{1.1} \\
&=& \frac{9}{11} \simeq 0.82
\end{eqnarray}
$$
参考書籍
統計学実践ワークブックは広大な範囲の準1級をカバーしているために、各トピックの内容は薄いです。そのため本章を理解するには以下の書籍も参考になると思います。



[…] 本章では、第$1$章でも扱った確率関数(probability function)について深めていきます。確率関数はデータの素性、対象のモデルを仮定するために必要な概念で統計的な分析や推論を行う上で非常に重要です。確率関数の具体例として$5,6$章で代表的な確率分布が紹介されます。また、それらを利用した推論などは$8$章以降となります。 […]