過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定準1級(2019.06)【正解と略解】(統計検定公式)
解答
[1] 解答
(1)
$\boxed{ \ \mathsf{1}\ }$ : ①
症例数 $n=475$ 帰無仮説 $H_0 : p=0.05$ の片側検定をするとき、検定統計量
$$
z=\frac{\hat p-p}{\sqrt{p(1-p)/n}}=\frac{\hat p-0.05}{\sqrt{0.05\times(1-0.05)/475}}=\frac{\hat p-0.05}{\sqrt{0.05\times0.95/475}}
$$
は、近似的に標準正規分布 $N(0,1)$ に従う。帰無仮説の下で $\hat p$ が $0.0733$ 以上になる確率は、
$$
\begin{align*}
P(\hat p \geqq 0.0733)&=P\left(\frac{\hat p-0.05}{\sqrt{0.05\times0.95/475}} \geqq \frac{0.0733-0.05}{\sqrt{0.05\times0.95/475}}\right)\\
&=P\left(\frac{\hat p-0.05}{\sqrt{0.05\times0.95/475}} \geqq 2.33\right)\\
&=0.0099 \fallingdotseq 0.01
\end{align*}
$$
(2)
$\boxed{ \ \mathsf{2}\ }$ : ④
症例数 $n$ として、問題文の片側検定を考える。
帰無仮説 $H_0 : p=0.05$ の下で $\hat p$ は正規分布 $N(0.05, (1-0.05)/n)$ に近似的に従い、有意水準 $2.5%$ のとき、棄却限界値は $0.05+Z_{0.025}\sqrt{0.05\times(1-0.05)/n}$ となる。
一方 、対立仮説 $H_1 : p=0.1$ の帰無仮説の下で $\hat p$ は正規分布 $N(0.1, (1-0.1)/n)$ に近似的に従い、検出力が $90\%$ のとき、棄却限界値は $0.1-Z_{(1-0.9)}\sqrt{0.1\times(1-0.1)/n}$となる。
ここで、 $Z_\alpha$ は 上側確率 $\alpha$ に対する標準正規分布のパーセント点を表し、標準正規分布の上側確率の表から $Z_{0.025}=1.96, Z_{0.1}=1.28$ である。
これらの条件を成立させるためには、
$$
\begin{align*}
0.05+Z_{0.025}\sqrt{0.05\times(1-0.05)/n} &\fallingdotseq 0.1-Z_{(1-0.9)}\sqrt{0.1\times(1-0.1)/n}\\
0.05+\frac{1.96\sqrt{0.05\times0.95}}{\sqrt{n}} &\fallingdotseq 0.1-\frac{1.28\sqrt{0.1\times0.9}}{\sqrt{n}}\\
\frac{1.96\sqrt{0.05\times0.95}+1.28\sqrt{0.1\times0.9}}{\sqrt{n}} &\fallingdotseq 0.1-0.05\\
\sqrt{n} &\fallingdotseq \frac{1.96\sqrt{0.05\times0.95}+1.28\sqrt{0.1\times0.9}}{0.1-0.05}\\
n &\fallingdotseq \left(\frac{1.96\sqrt{0.05\times0.95}+1.28\sqrt{0.1\times0.9}}{0.1-0.05}\right)^2\\
n &\fallingdotseq 263.2
\end{align*}
$$
[2] 解答
(1)
$\boxed{ \ \mathsf{3}\ }$ : ③
発現割合が $0.05$ の事象について、独立に $8$ 症例調べたとき、「少なくとも $1$ 例の有害事象が観測される」ということは、「有害事象が$8$ 症例中全く観測されない」ことではないことから、その確率は、$1-(1-0.05)^8 \fallingdotseq 0.34$ となる。
(2)
$\boxed{ \ \mathsf{4}\ }$ : ⑤
発現割合が $0.001$ の事象について、独立に $n$ 症例調べたとき、「少なくとも $1$ 例の有害事象が観測される」ということは、「有害事象が$n$ 症例中全く観測されない」ことではないことから、
$$
\begin{align*}
1-(1-0.001)^n &= 95\% \\
(1-0.001)^n &= 1-0.95 \\
n\log (1-0.001) &= \log 0.05\\
n &= \frac{\log 0.05}{\log (1-0.001)}
\end{align*}
$$
ここで、$\log (1-\varepsilon) \simeq -\varepsilon$ を使って、$\log (1-0.001) \simeq -0.001$
$$
\therefore n = \frac{\log 0.05}{-0.001} = \frac{2.3026\log_{10} (5/10^2)}{-0.001}= \frac{2.3026 \times (0.669 – 2)}{-0.001} \fallingdotseq 3065
$$
解説
母比率の検定
(「統計検定2級対応 統計学基礎」 p.148, p.118 参照)
大きさ $n$ の標本のうち母比率 $p$ の対象に該当する標本の数 $X$ の分布は二項分布 $B(n,p)$ に従うと考えられる。その期待値と分散は $E[x]=np,\ V[x]=np(1-p)$
$n$ が大きいとき、中心極限定理によって、次の $z$ は標準正規分布 $N(0,1)$ で近似できる。
$$
z=\frac{X-np}{\sqrt{np(1-p)}}
$$
ここで,標本比率は $\hat p=X/n$で求められるため、上式は次のように変形できる。
$$
z=\frac{\hat p-p}{\sqrt{p(1-p)/n}}
$$
したがって、母比率の検定では、帰無仮説 $H_0 : p=p_0$ の下で、次の統計検定量 $z$ が標準正規分布に従うものとして検定を行う。
$$
z=\frac{\hat p-p_0}{\sqrt{p_0(1-p_0)/n}}
$$
検定の過誤
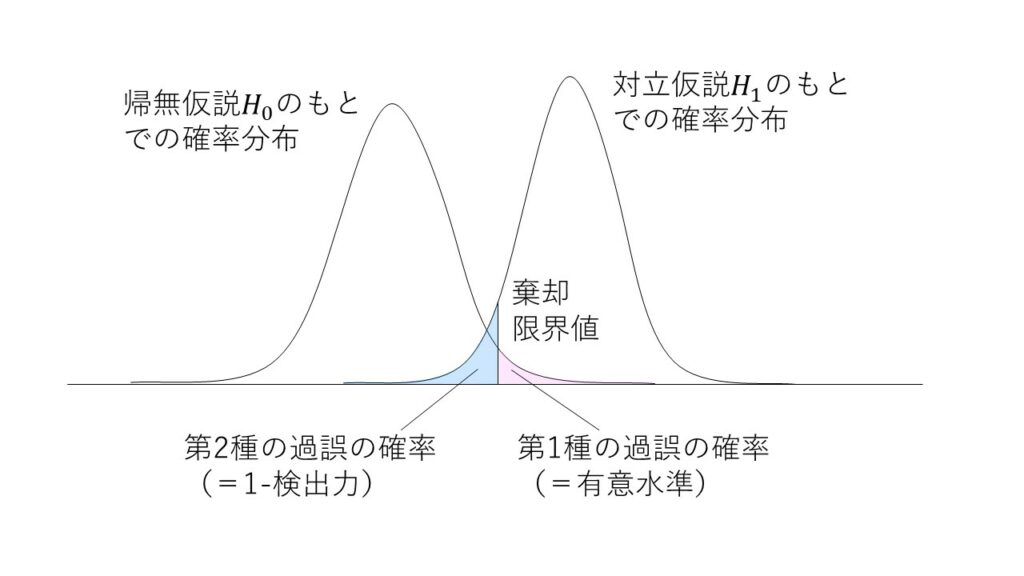
統計的仮説検定においては、帰無仮説(否定したい仮説)と対立仮説(検証したい仮説)の相反する2つの仮説を立てて検定を行う。したがって次の2種類の誤りが生じ得る。
- 第1種の過誤・・帰無仮説が正しいのに帰無仮説を棄却する過誤
この過誤を犯す確率を有意水準という。(第1種の過誤を犯す確率=有意水準) - 第2種の過誤・・対立仮説が正しいのに帰無仮説を棄却しない過誤
この過誤を犯さない確率を検出力という。(第2種の過誤を犯す確率=$1-$検出力)
これらの2種類の過誤は、帰無仮説が棄却されるぎりぎりの値である棄却限界値を境にトレードオフの関係にあり、第1種の過誤の確率を小さくすると第2種の過誤の確率は大きくなり、逆に第1種の過誤の確率を大きくすると第2種の過誤の確率は小さくなる。