過去問題
過去問題は統計検定公式が問題と解答例を公開しています。こちらを参照してください。
解答
[1]解答
$\boxed{ \ \mathsf{20}\ }$:①
結合されている終端ノードの距離は(ア),(イ)のいずれでも同じである.$A,B$の距離は$2$であり,表2から距離$2$なのは生徒$1$と生徒$2$の間だけなので,$A,B$が生徒$1$,$2$だとわかる.次に$D,E$の距離をみると約$1.5$であることが表2からわかる.生徒$3~5$の間で距離が$1.5$に近いのは生徒$4$と生徒$5$の$\sqrt{2}$であるからこれもわかる.最後に残ったのが$C$が生徒$3$である.
(ア)において,クラスター$\{A,B\}$と$C$がクラスターを形成しており,その距離は$2$より少し大きい.ここで,$A$と$C$の距離(つまり,生徒$1$と生徒$3$)及び,$B$と$C$(つまり生徒$2$と生徒$3$)の距離はそれぞれ,$\sqrt{17}$,$\sqrt{5}$となっている.$\sqrt{5} \approx 2.2$であるから(ア)が最近隣法であるとわかる.したがって,(イ)は最遠隣法となる.
[2]解答
(1) $\boxed{ \ \mathsf{21}\ }$:①
クラスター中心とそれに対応するクラスターは次のように変化する.
| クラスター中心 | クラスター | |
| 初期点 | $(10,10)$,$(10,8)$ | $\{ 1 \}$,$\{2,3,4,5\}$ |
| 1回目の変化 | $(10,10)$,$(8,7.25)$ | $\{1,2\}$, $\{3,4,5\}$ |
| 2回目の変化 | $(10,9)$,$(7.3,7)$ | $\{1,2\}$, $\{3,4,5\}$ |
まず,初期点に対するクラスターを考える.下図から明らかに生徒$3$,$4$,$5$は生徒$1$よりも生徒$2$に近い.よって初期点に対して割当てられたクラスターは$\{1\}$,$\{2,3,4,5\}$である.
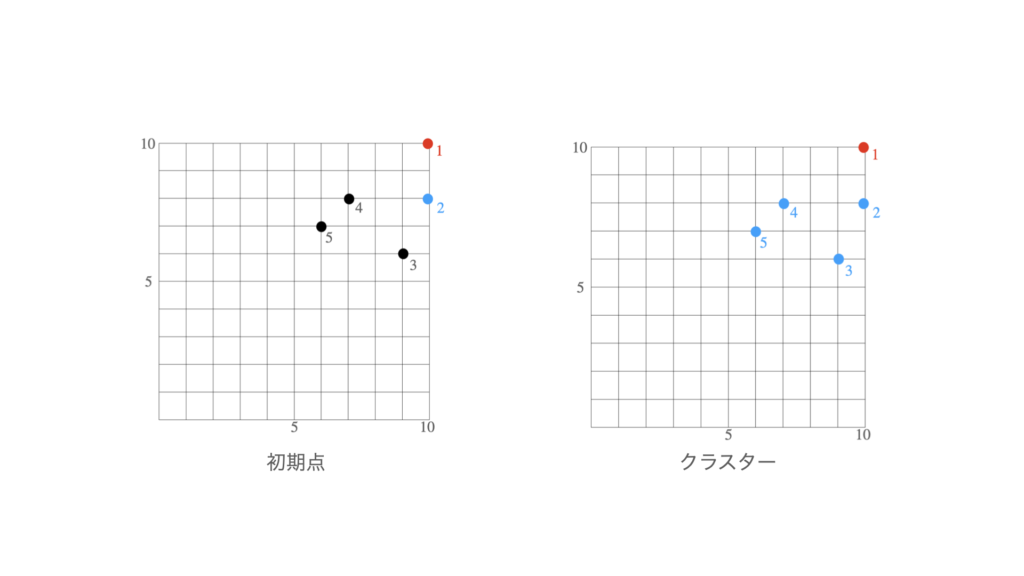
次に,このクラスターから新しいクラスター中心を求める(1回目の変化).クラスター$\{1\}$の中心は変化せず$(10,10)$である(赤い点).クラスター$\{2,3,4,5\}$に対応する中心は,
\[
\left( \dfrac{10+9+7+6}{4}, \dfrac{8+6+8+7}{4} \right)= (8,7.25)
\]
である(青い点).すると,生徒$1$,$2$が赤い点を中心とするクラスターに属し,生徒$3$,$4$,$5$が青い点を中心とするクラスターに属することがわかる.
したがって,出力されるクラスターは$\{1,2\}$,$\{3,4,5\}$である.
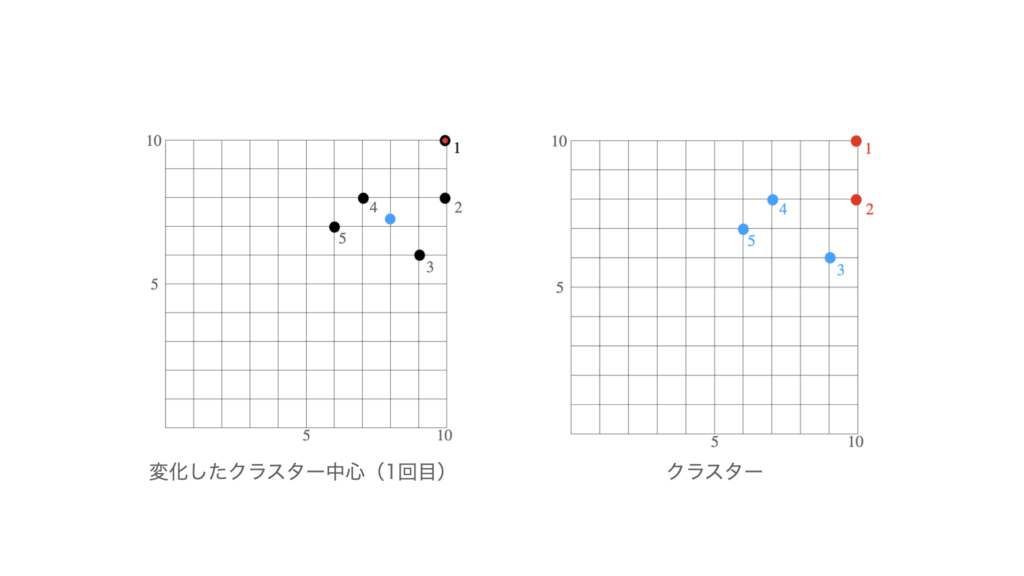
(2回目の変化)クラスター$\{1,2\}$,$\{3,4,5\}$に対応するクラスター中心はそれぞれ$(10,9)$,$(7.3,7)$である.これから出力されるクラスターは$\{1,2\}$,$\{3,4,5\}$であり変化しない.
以上から,出力されるクラスターは$\{1,2\}$,$\{3,4,5\}$である.
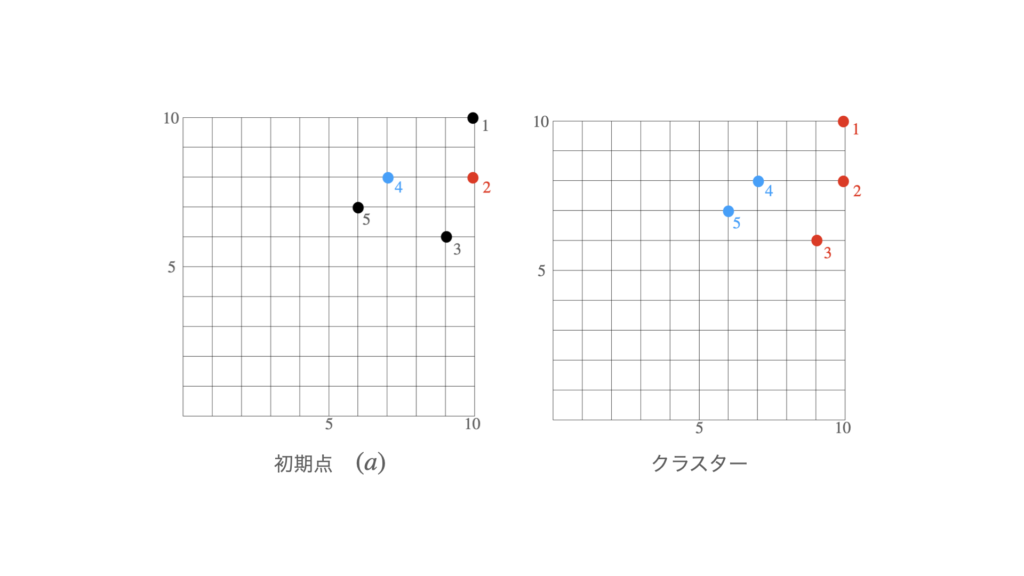
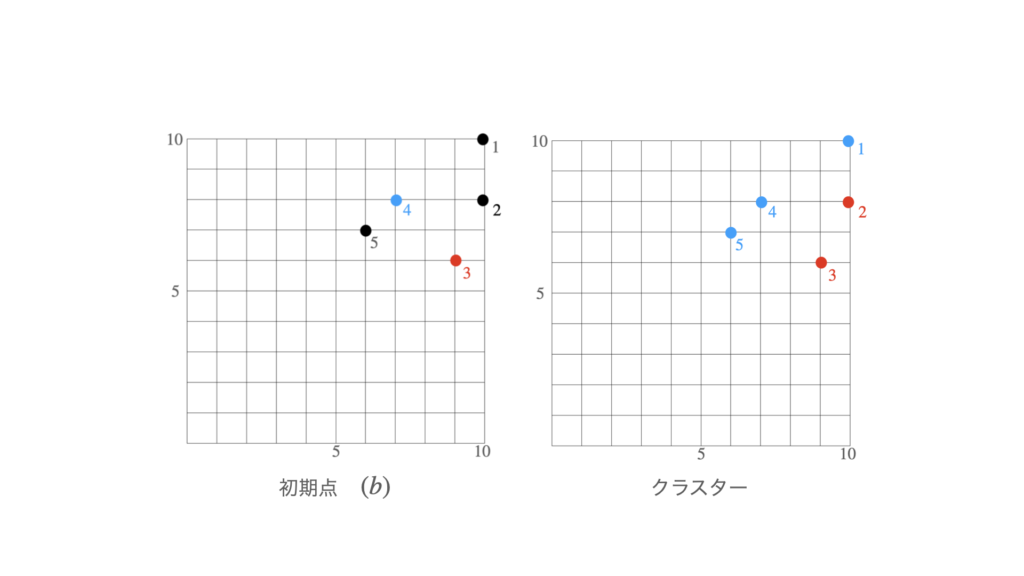
(2) $\boxed{ \ \mathsf{22}\ }$:④
下の図から初期点が$(a)$のときはクラスターは$\{1,2,3\}$,$\{4,5\}$となり,初期点が$(b)$のときは$\{1,4,5\}$,$\{2,3\}$となる.