「統計検定$2$級 公式問題集 CBT対応版」の解答例を取りまとめるにあたって、当記事では「PART.$2$ 分野・項目別 問題・解説」のCategory.$5$「確率分布」の解答例を作成しました。解答例は「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
解答例
Q.1
$$
\large
\begin{align}
f(x) &= a \left( 1 – \frac{x}{20} \right) \quad (0 \leq x \leq 20) \\
&= 0 \qquad (\mathrm{Otherwise})
\end{align}
$$
上記の$f(x)$が確率密度関数であるので、$\displaystyle \int_{-\infty}^{\infty} f(x) dx = 1$が成立しなくてはならない。よって、下記のように考えることができる。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} f(x) dx &= \int_{0}^{20} a \left( 1 – \frac{x}{20} \right) dx \\
&= a \left[ x – \frac{x^2}{40} \right]_{0}^{20} \\
&= a \left( 20 – \frac{20^2}{40} \right) \\
&= a (20 – 10) \\
&= 10a = 1 \\
a &= \frac{1}{10}
\end{align}
$$
上記より$\displaystyle a = \frac{1}{10}$の④が正しい。
Q.2
$X \sim \mathcal{N}(2,3^2)$より、$P(-1 < X \geq 4)$は$Z \sim \mathcal{N}(0,1)$である$Z$を用いて下記のように表すことができる。
$$
\large
\begin{align}
P(-1 < X \geq 4) &= P \left( \frac{-1-2}{3} < \frac{X-2}{3} \geq \frac{4-2}{3} \right) \\
&= P \left( -1 < Z \geq \frac{2}{3} \right) \\
&= 1 – 0.1587 – \left( \frac{1}{3} \cdot 0.2546 + \frac{2}{3} \cdot 0.2514 \right) \\
&= 1 – 0.1587 – 0.252 \\
&= 0.589
\end{align}
$$
上記より$0.59$の⑤が正しい。
Q.3
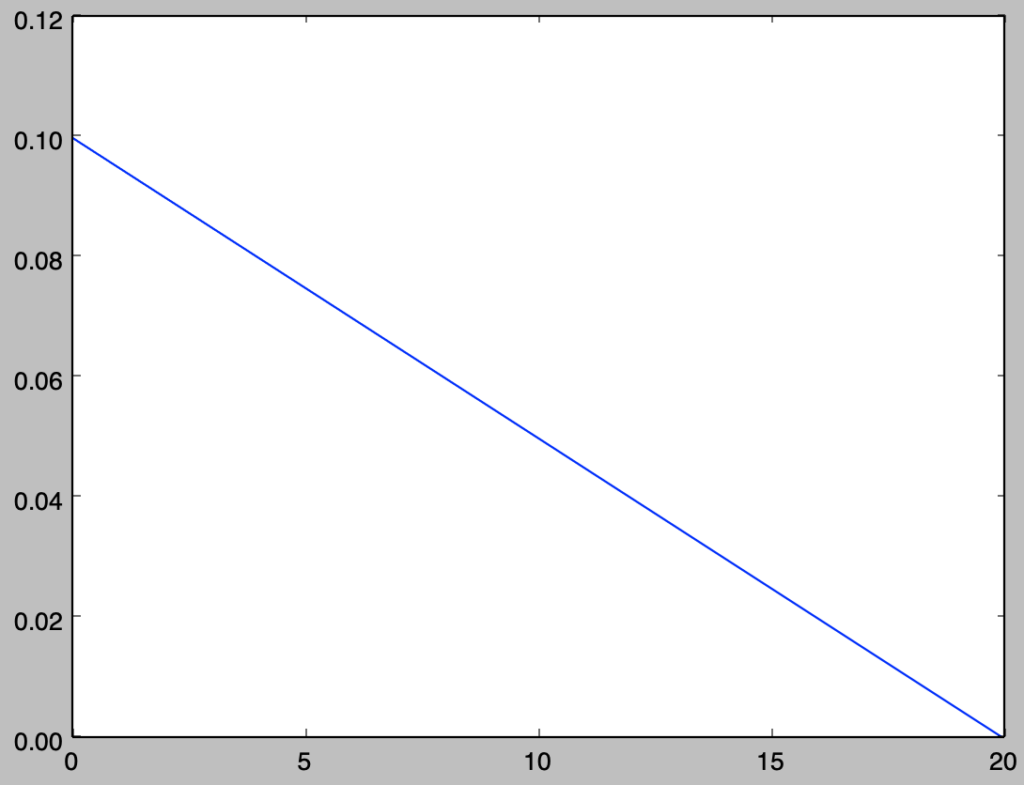
確率密度関数$f(x)$は上記のように図示できる。ここで水道料金は$0 \leq x \leq 10$で$1,000$円、$10 \leq x \leq 15$で$1,120$円、$15 \leq x \leq 20$で$1,280$円であるので、期待値$E[X]$は下記のように計算できる。
$$
\large
\begin{align}
E[X] &= \int_{0}^{10} 1000 f(x) dx + \int_{0}^{10} 1120 f(x) dx + \int_{0}^{10} 1280 f(x) dx \\
&= 1000 \left( \frac{20 \cdot 0.1}{2} – \frac{10 \cdot 0.05}{2} \right) + 1120 \left( \frac{10 \cdot 0.05}{2}-\frac{5 \cdot 0.025}{2} \right) + 1280 \cdot \frac{5 \cdot 0.025}{2} \\
&= 1000 \times \frac{3}{4} + 1120 \times \frac{3}{16} + 1280 \times \frac{1}{16} \\
&= 750 + 70 \times 3 + 80 \\
&= 1040
\end{align}
$$
上記より②が正解である。
・考察
確率密度関数に基づく三角形の面積が$\displaystyle 1:\frac{1}{4}:\frac{1}{16}$であることに着目すると計算しやすい。
Q.4
標本比率$\hat{p}$に関して下記が成立する。
$$
\large
\begin{align}
\hat{p} \sim \mathcal{N} \left( p,\frac{\hat{p}(1-\hat{p})}{n} \right)
\end{align}
$$
よって$Z \sim \mathcal{N}(0,1)$である確率変数$Z$を用いて$P(|\hat{p}-p| \leq 0.1)$は下記のように計算できる。
$$
\large
\begin{align}
P(|\hat{p}-p| \leq 0.1) &= P(-0.1 \leq \hat{p}-p \leq 0.1) \\
&= P \left( -\frac{0.1}{\sqrt{\hat{p}(1-\hat{p})/n}} \leq \frac{\hat{p}-p}{\sqrt{\hat{p}(1-\hat{p})/n}} \leq \frac{0.1}{\sqrt{\hat{p}(1-\hat{p})/n}} \right) \\
&= P \left( -\frac{0.1}{\sqrt{0.54(1-0.54)/100}} \leq Z \leq \frac{0.1}{\sqrt{0.54(1-0.54)/100}} \right) \\
& \simeq P( -2.01 \leq Z \leq 2.01) \\
& \simeq 1 – 2 \times 0.0222 = 0.9556
\end{align}
$$
上記より正解は⑤である。
Q.5
$2$以下の目が出る確率を$p$とおくと、$X \sim \mathrm{Bin}(7,p)$より下記が成立する。
$$
\large
\begin{align}
P(X=x) &= {}_{7} C_{x} p^{x} (1-p)^{7-x} \\
P(X=x+1) &= {}_{7} C_{x} p^{x+1} (1-p)^{6-x}
\end{align}
$$
このとき$\displaystyle \frac{P(X=x+1)}{P(X=x)}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{P(X=x+1)}{P(X=x)} &= \frac{{}_{7} C_{x} p^{x+1} (1-p)^{6-x}}{{}_{7} C_{x} p^{x} (1-p)^{7-x}} \\
&= \frac{7!}{(x+1)!(6-x)!} \times \frac{x!(7-x)!}{7!} \times \frac{p}{1-p} \\
&= \frac{7-x}{x+1} \times \frac{p}{1-p}
\end{align}
$$
上記に$\displaystyle p = \frac{1}{3}$を代入すると下記が得られる。
$$
\large
\begin{align}
\frac{P(X=x+1)}{P(X=x)} &= \frac{7-x}{x+1} \times \frac{p}{1-p} \\
&= \frac{7-x}{x+1} \times \frac{1}{3} \times \frac{3}{2} \\
&= \frac{-x+7}{2x+2}
\end{align}
$$
上記より②が正解である。
Q.6
Ⅰ 右に裾の長い分布では歪度は正の値であり、左に裾が長い分布では歪度は負の値であるので×
Ⅱ 尖度は中心部の尖り具合の指標であるので×
Ⅲ 自由度が大きいほど尖度の絶対値は小さくなり、$n \to \infty$で正規分布に収束するので×
上記より正解は⑤である。
Q.7
$X \sim \mathcal{N}(4000,500^2), Y \sim \mathcal{N}(4000,500^2)$のとき、$X-Y \sim \mathcal{N}(0,2 \cdot 500^2)$が成立する。よって確率$P(X-Y \geq 800)$は下記のように計算できる。
$$
\large
\begin{align}
P(X-Y \geq 800) &= P \left( Z \geq \frac{800}{500 \sqrt{2}} \right) \\
&= P( Z \geq 1.13 \cdots ) \\
&= 0.1292
\end{align}
$$
よって正解は③である。
Q.8
$$
\large
\begin{align}
E[X] &= 2.0, \, E[Y] = 3.0, \, E[XY] = 6.3, \, V[X] = 1.0, \, V[Y] = 1.0 \\
U &= 3X-2, \, V = -2Y-4
\end{align}
$$
上記に基づいて$E[U], E[V], E[UV]$は下記のように計算できる。
$$
\large
\begin{align}
E[U] &= E[3X-2] \\
&= 3E[X]-2 = 4 \\
E[V] &= E[-2Y-4] \\
&= -2E[Y]-4 = -10 \\
E[UV] &= E[(3X-2)(-2Y-4)] \\
&= – 6E[XY] – 12E[X] + 4E[Y] + 8 \\
&= -41.8
\end{align}
$$
よって共分散$\mathrm{Cov}[U,V]$は下記のように計算できる。
$$
\large
\begin{align}
\mathrm{Cov}[U,V] &= E[UV] – E[U]E[V] \\
&= -41.8 – 4 \times (-10) \\
&= -1.8
\end{align}
$$
また、$V[U], V[V]$は下記のように計算できる。
$$
\large
\begin{align}
V[U] &= V[3X-2] \\
&= 3^2 V[X] \\
&= 9 \\
V[V] &= V[-2Y-4] \\
&= (-2)^2 V[Y] \\
&= 4
\end{align}
$$
したがって相関係数$r[U,V]$は下記のように計算できる。
$$
\large
\begin{align}
r[U,V] &= \frac{\mathrm{Cov}[U,V]}{\sqrt{V[U]V[V]}} \\
&= \frac{-1.8}{3 \times 2} \\
&= -0.3
\end{align}
$$
以上より正解は④である。
参考
・【統計検定$2$級対応】統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
