当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$7$の「関数の展開」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。
・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook_math#math_stat
本章のまとめ
演習問題解答
問題$7.1$
$\displaystyle f(x) = \frac{1}{x+a} = (x+a)^{-1}$の導関数は下記のように計算できる。
$$
\large
\begin{align}
f'(x) &= -(x+a)^{-2} \\
f^{”}(x) &= 2!(x+a)^{-3} \\
f^{(3)}(x) &= -3!(x+a)^{-4} \\
f^{(4)}(x) &= 4!(x+a)^{-5} \\
f^{(5)}(x) &= -5!(x+a)^{-6} \\
& \vdots
\end{align}
$$
よって$\displaystyle f(x) = \frac{1}{x+a} = (x+a)^{-1}$のテイラー展開は下記のように得られる。
$$
\large
\begin{align}
f(x) &= f(0) + \frac{f'(0)}{1!}x + \frac{f^{”}(0)}{2!}x^2 + \frac{f^{(3)}(0)}{3!}x^3 \cdots \\
&= a^{-1} + \frac{-a^{-2}}{1!}x + \frac{2!a^{-3}}{2!}x^2 + \frac{-3!a^{-4}}{3!}x^3 \cdots \\
&= \frac{1}{a} – \frac{1}{a^2}x + \frac{1}{a^3}x^2 – \frac{1}{a^4}x^3 \cdots , \quad |x|<|a|
\end{align}
$$
問題$7.2$
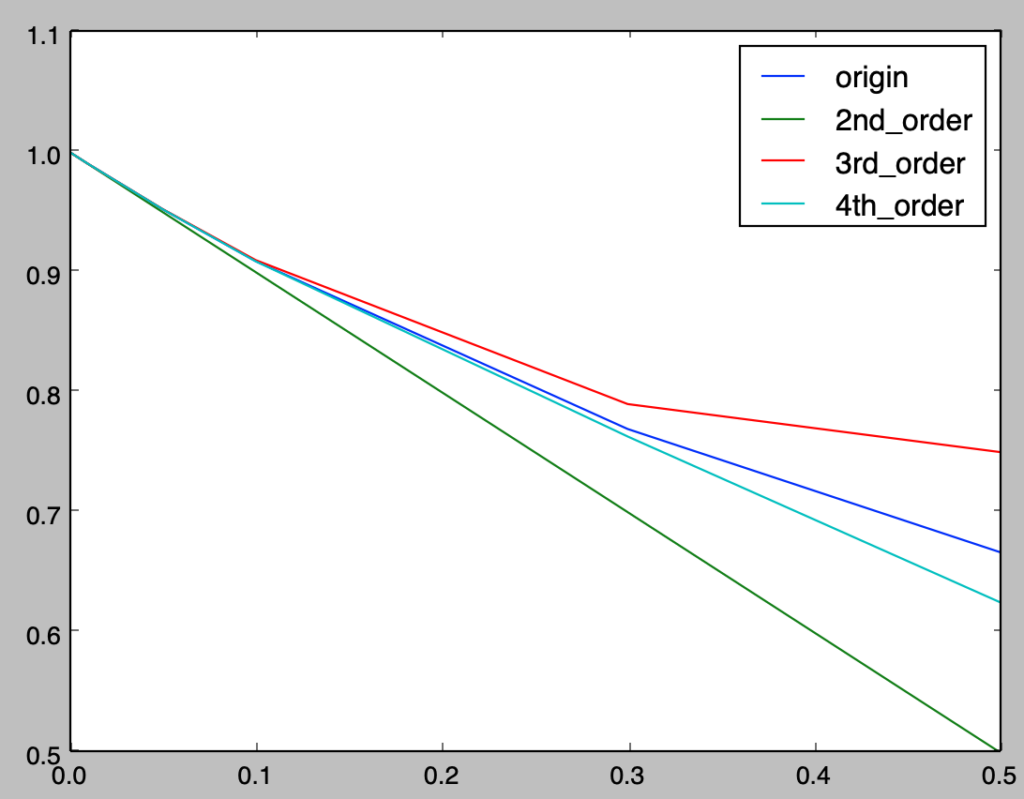
下記のような結果が得られる。
| $x$ | 真値 | 第$2$項まで | 第$3$項まで | 第$4$項まで |
| $0.5$ | $0.66666667$ | $0.5$ | $0.75$ | $0.625$ |
| $0.3$ | $0.76923077$ | $0.7$ | $0.79$ | $0.763$ |
| $0.1$ | $0.9090909$ | $0.9$ | $0.91$ | $0.909$ |
| $0.05$ | $0.95238095$ | $0.95$ | $0.9525$ | $0.952375$ |
| $0.01$ | $0.9900990$ | $0.99$ | $0.9901$ | $0.990099$ |
| $0$ | $1$ | $1$ | $1$ | $1$ |
詳しい計算やグラフの描画は下記を実行することで行うことができる。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.5, 0.3, 0.1, 0.05, 0.01, 0.])
a = 1.
f_x = np.zeros([6,4])
f_x[:,0] = 1/(x+a)
f_x[:,1] = 1/a - x/a**2
f_x[:,2] = 1/a - x/a**2 + x**2/a**3
f_x[:,3] = 1/a - x/a**2 + x**2/a**3 - x**3/a**4
print(f_x)
label_line = ["origin", "2nd_order", "3rd_order", "4th_order"]
for i in range(f_x.shape[1]):
plt.plot(x, f_x[:,i], label=label_line[i])
plt.legend()
plt.show()・実行結果
[[ 0.66666667 0.5 0.75 0.625 ]
[ 0.76923077 0.7 0.79 0.763 ]
[ 0.90909091 0.9 0.91 0.909 ]
[ 0.95238095 0.95 0.9525 0.952375 ]
[ 0.99009901 0.99 0.9901 0.990099 ]]