階乗・順列(Permutation)・組合せ(Combination)の定義と直感的理解

当記事では「統計学を学ぶにあたって最低限抑えておきたい数学」の中から「階乗・順列(Permutation)・組合せ(Combination)」に関して取り扱います。順列と組合せが混同されやすいので、可能な限り直感的な理解ができるように取りまとめを行いました。
取りまとめにあたっては数学の解説に関してはなるべくシンプルに取り扱いますが、統計学への応用に関連した複雑な内容に関しては目次に「*」をつけました。「*」がついているものはやや難しいので、読み飛ばしても問題ありません。

・基本数学まとめ
https://www.hello-statisticians.com/math_basic

階乗

概要

$$
\large
\begin{align}
n! = 1 \times 2 \times 3 \times \cdots \times (n-1) \times n
\end{align}
$$

自然数$n$の階乗$n!$は上記のように定められます。階乗に基づいて$n$人の並べ方を計算することができます。

直感的理解

階乗の直感的理解にあたっては、「$n$人の並べ替え」を元に考えると良いです。「並べ替え」を考える場合は、$n$個の場所を先に考えて、「それぞれの場所に人を割り振る」イメージを持つとわかりやすいです。

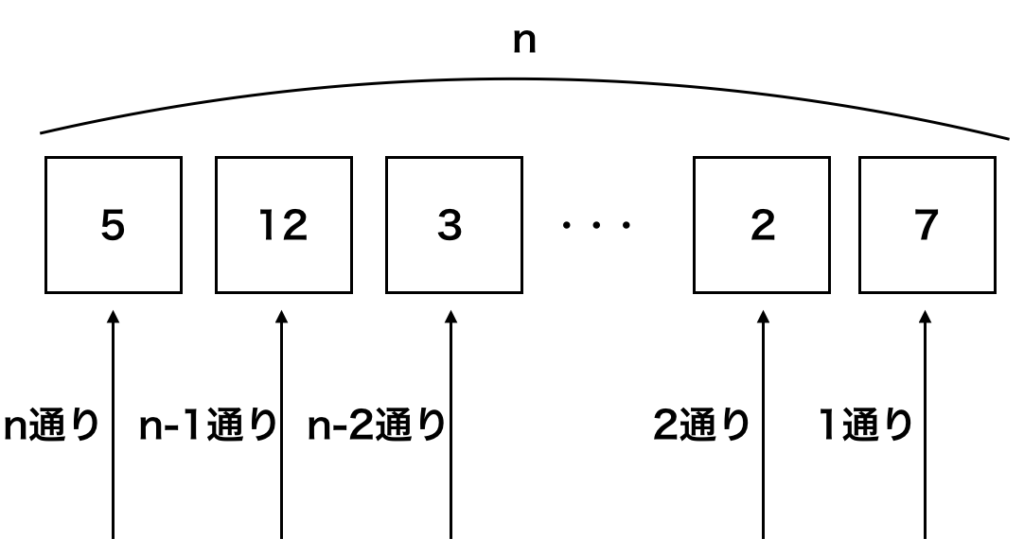
たとえば$n$人にそれぞれ$1$〜$n$の番号を割り振るとき、上図では$1$番目の場所には$n$通りの中から$5$を選び割り振りが行われます。このことにより、$2$番目の場所には$5$以外の$n-1$通りから$12$が選ばれ、同様に$n$番目の場所まで割り振りを行います。

$n-1$番目の場所には$2,7$から$2$、$n$番目の場所には残った$7$が対応します。このように考えるとき、全体の並べ方は$n!$通りに対応すると考えることができます。

順列

概要

$$
\large
\begin{align}
{}_{n} P_m = (n-m+1) \times (n-m+2) \times (n-m+3) \times \cdots \times (n-1) \times n
\end{align}
$$

自然数$m, n, \, n \geq m$に関して順列${}_{n} P_{m}$は上記のように定められます。上記の式に基づいて$n$人の中から$m$人を選んで並べる際の並べ方などの計算を行うことができます。

直感的理解

順列の直感的理解は階乗の図と同様に行うことができます。

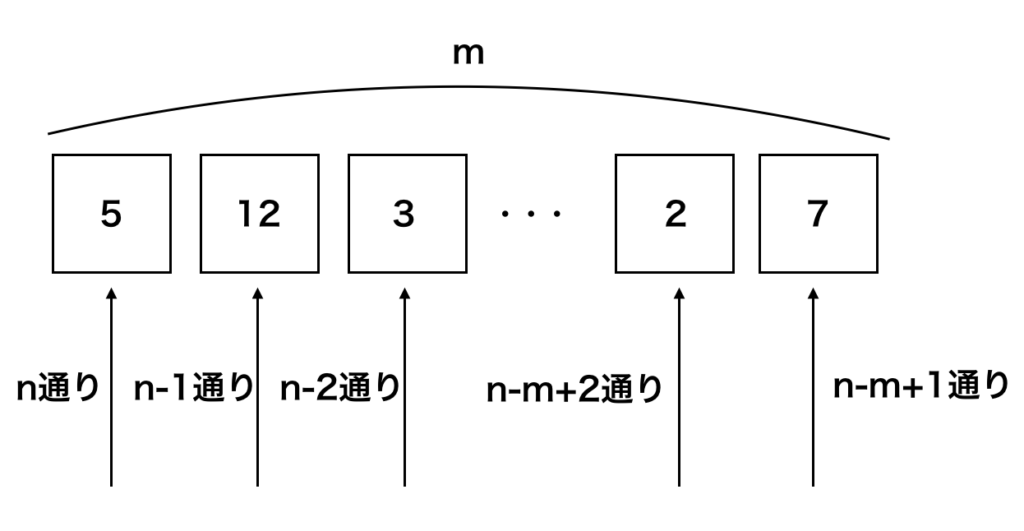
階乗の図では$n$個の場所を用意し、$n$人と対応させましたが、順列では「$m$個の場所に対応させる」と考えれば良いです。

組合せ

概要

$$
\large
\begin{align}
{}_{n} C_m = \frac{(n-m+1) \times (n-m+2) \times (n-m+3) \times \cdots \times (n-1) \times n}{m!}
\end{align}
$$

自然数$m, n, \, n \geq m$に関して組合せ${}_{n} C_{m}$は上記のように定められます。上記の式に基づいて$n$人の中から$m$人を選ぶ際の組合せを計算することができます。

直感的理解

組合せの直感的理解にあたっては「順列」の図で並べ替えを行わない場合を考えれば良いです。重複が$m!$通りあるので、順列の式を$m!$で割った式が組合せの式に一致します。