ロジスティック回帰などに関連してオッズ(odds)という考え方が用いられますが、教科書などの解説ではオッズそのものの取り扱いがあまり多くありません。そこで当記事ではオッズという考え方を中心に取り扱い、一般的な使用例も確認しながら具体的に理解できるように取りまとめを行いました。
作成にあたってはWikipediaのオッズのまとめや「統計学実践ワークブック」の$18$章「質的回帰」、$28$章「分割表」などを参考にしました。
・オッズ Wikipedia
オッズの概要
オッズの定義
ある事象が起こる確率を$p$、起こらない確率を$1-p$とするとき、下記のようにオッズ$\mathrm{Odds}$を定義する。
$$
\large
\begin{align}
\mathrm{Odds} = \frac{p}{1-p}
\end{align}
$$
定義域の$0 \leq p < 1$において上記は$p$に関する単調増加関数であり、式定義より$0 \leq \mathrm{Odds} < \infty$が成立する。式だけだと少々わかりにくいので、下記のPythonを実行することでオッズのグラフを描くことができる。
import numpy as np
import matplotlib.pyplot as plt
p = np.arange(0.,1.,0.05)
odds = p/(1-p)
plt.plot(p,odds)
plt.show()・実行結果
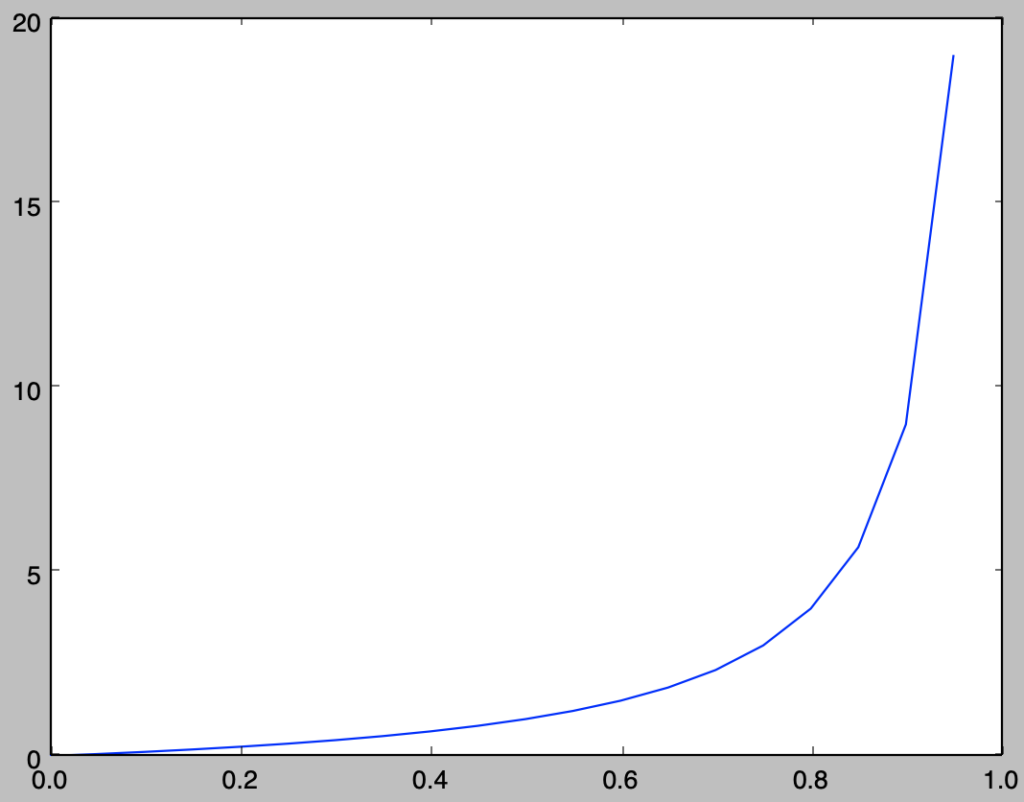
オッズの一般的な使用例
オッズは競馬などの賭けを行う際の儲けの計算に伝統的に用いられてきた。たとえば$5$回に$1$回に$A$、$5$回に$4$回に$B$が起こる場合を考える。このとき$A$が起こるオッズの$\mathrm{Odds}_{A}$と$B$が起こるオッズ$\mathrm{Odds}_{B}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\mathrm{Odds}_{A} &= \frac{0.2}{1-0.2} = 0.25 \\
\mathrm{Odds}_{B} &= \frac{0.8}{1-0.8} = 4
\end{align}
$$
上記のようにオッズを計算する場合、オッズの逆数$+1$が取り分の倍率となる。
一方で競馬などでのオッズは「払戻金」を「的中券$100$円分に対する金額」で表現される。これをパリミュチュエル方式という。
$\displaystyle \mathrm{Odds} = \frac{p}{1-p}$で定義されるオッズは的中時の倍率を重視する一般的な用法と少々異なるので注意が必要であると考えられる。
統計学におけるオッズの取り扱い
ロジスティック回帰とオッズ
「ロジスティック回帰」は「事象が生じる確率を予測する回帰に対応する」と解釈することができる。事象を表す確率変数を$Y$と定義し、$y_1,…,y_n$が観測されると考える。
$$
\large
\begin{align}
\pi_{i} &= \hat{y}_i = \frac{1}{1+\exp{(f(x_i))}} \quad (1) \\
f(x_i) &= \beta_0 + \beta_1 x_{i1} + … + \beta_{k} x_{ik}
\end{align}
$$
ここで上記の$(1)$式を$\exp{(f(x_i))}$に関して解くことを考える。
$$
\large
\begin{align}
\pi_{i} &= \frac{1}{1+\exp{(-f(x_i))}} \\
\pi_{i} &= \frac{\exp{(f(x_i))}}{\exp{(f(x_i))}+1} \\
\pi_{i}(1+\exp{(f(x_i))}) &= \exp{(f(x_i))} \\
\pi_{i} + \pi_{i} \exp{(f(x_i))} &= \exp{(f(x_i))} \\
\pi_{i} &= (1-\pi_{i}) \exp{(f(x_i))} \\
\frac{\pi_{i}}{1-\pi_{i}} &= \exp{(f(x_i))} \quad (2)
\end{align}
$$
$(2)$式より$\exp{(f(x_i))} = \exp{(\beta_0 + \beta_1 x_{i1} + … + \beta_{k} x_{ik})} = \exp{\beta_0} \exp{\beta_1 x_{i1}}…\exp{\beta_{k} x_{ik})}$は確率のオッズに対応することが読み取れる。
また、$\exp{(f(x_i))}$は下記のように表すことができる。
$$
\large
\begin{align}
\exp{(f(x_i))} &= \exp{(\beta_0 + \beta_1 x_{i1} + … + \beta_{k} x_{ik})} \\
&= e^{\beta_0} e^{\beta_1 x_{i1}}…e^{\beta_{k} x_{ik}} \quad (3)
\end{align}
$$
$(2), (3)$式より$\exp{(f(x_i))} = e^{\beta_0} e^{\beta_1 x_{i1}}…e^{\beta_{k} x_{ik}}$は「確率変数$Y$に関する事象が観測される確率」のオッズに対応することが読み取れる。
分割表とオッズ比
分割表における$2$群の一様性などを考えるにあたって、オッズの比率のオッズ比を考える。
