当記事は「経済・ファイナンスデータの計量時系列分析(朝倉書店)」の読解サポートにあたってChapter.1の「時系列分析の基礎概念」の章末問題の解説について行います。
基本的には書籍の購入者向けの解答例・解説なので、まだ入手されていない方は入手の上、ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。(そのため著者の意図とは異なる解説となる可能性はあります)
また、下記に公式の解答があるので、こちらも合わせて参照ください。
https://www.asakura.co.jp/user_data/contents/12792/3.pdf
章末の演習問題について
問題1.1の解答例
ラグ$k$の自己共分散$\gamma_{k}$に関して下記が成立する。
$$
\large
\begin{align}
\gamma_{k} = Cov(y_t, y_{t-k}) = Cov(y_{t-k}, y_t) = \gamma_{-k}
\end{align}
$$
上記より、$\gamma_{k}=\gamma_{-k}$が成立することが確認できる。
問題1.2の解答例
$$
\large
\begin{align}
y_{t} = \mu + \epsilon_{t}, \quad \epsilon_{t} \sim W.N.(\sigma^2)
\end{align}
$$
上記で表した$(1.8)$式の確率過程の平均$E[Y_t]$、分散$V[Y_t]$、自己共分散$Cov[Y_t,Y_{t-k}]$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
E[Y_t] &= E[\mu + \epsilon_{t}] = \mu \\
V[Y_t] &= V[\mu + \epsilon_{t}] \\
&= V[\epsilon_{t}] = \sigma^2 \\
Cov[Y_t,Y_{t-k}] &= Cov[\mu + \epsilon_{t},\mu + \epsilon_{t-k}] \\
&= Cov[\epsilon_{t},\epsilon_{t-k}] = 0
\end{align}
$$
上記より、式$(1.8)$は定常過程と考えることができる。
問題1.3の解答例
下記を実行することで図$1.3$と同様の結果が得られる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
mu = np.array([0., 2., -2., 0., 0., 2.])
sigma = np.array([1., 1., 1., 2., 3., 2.])
x = np.arange(0,100,1)
y = np.zeros([x.shape[0],mu.shape[0]])
for i in range(x.shape[0]):
y[i,:] = mu + stats.norm.rvs(0,sigma,size=6)
for i in range(6):
plt.subplot(2,3,i+1)
plt.plot(x,y[:,i])
plt.title("mu={}, sigma={}".format(mu[i],sigma[i]))
plt.legend()
plt.show()・実行結果
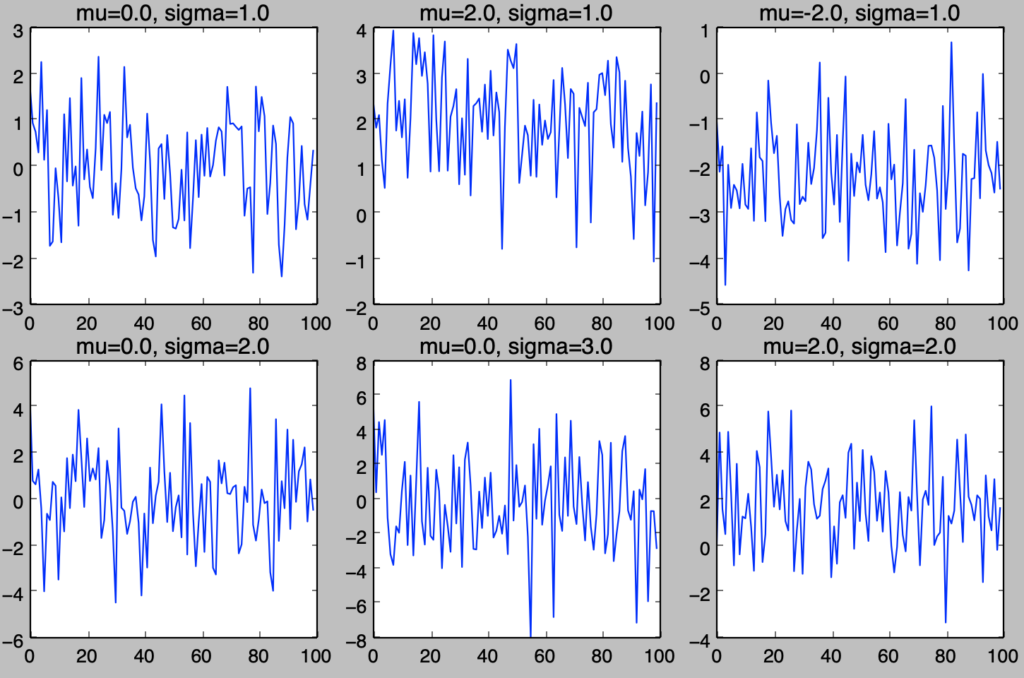
問題1.4の解答例
平均と分散が等しいいくつかの分布を用意し、$t$に関して何らかの規則に基づいて$y_t$が異なる分布に基づいて生成されるようにすることで、$y_t$は弱定常過程にはなるが強定常過程にはならない。
