数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事では回帰の理解にあたって、単回帰、重回帰、ロジスティック回帰、プロビット回帰、ポアソン回帰などのPythonでの実装を取り扱いました。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
線形回帰
単回帰のパラメータ推定
サンプルの生成
$y_i = 0.7 + 2.1x_i + \epsilon_i, \quad \epsilon_i \sim N(0,1)$に基づいてサンプルの生成を行い、散布図を描画するにあたっては、以下を実行すれば良い。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x = 10*np.random.rand(100)
y = 0.7 + 2.1*x + stats.norm.rvs(size=100)
plt.scatter(x,y)
plt.show()・実行結果
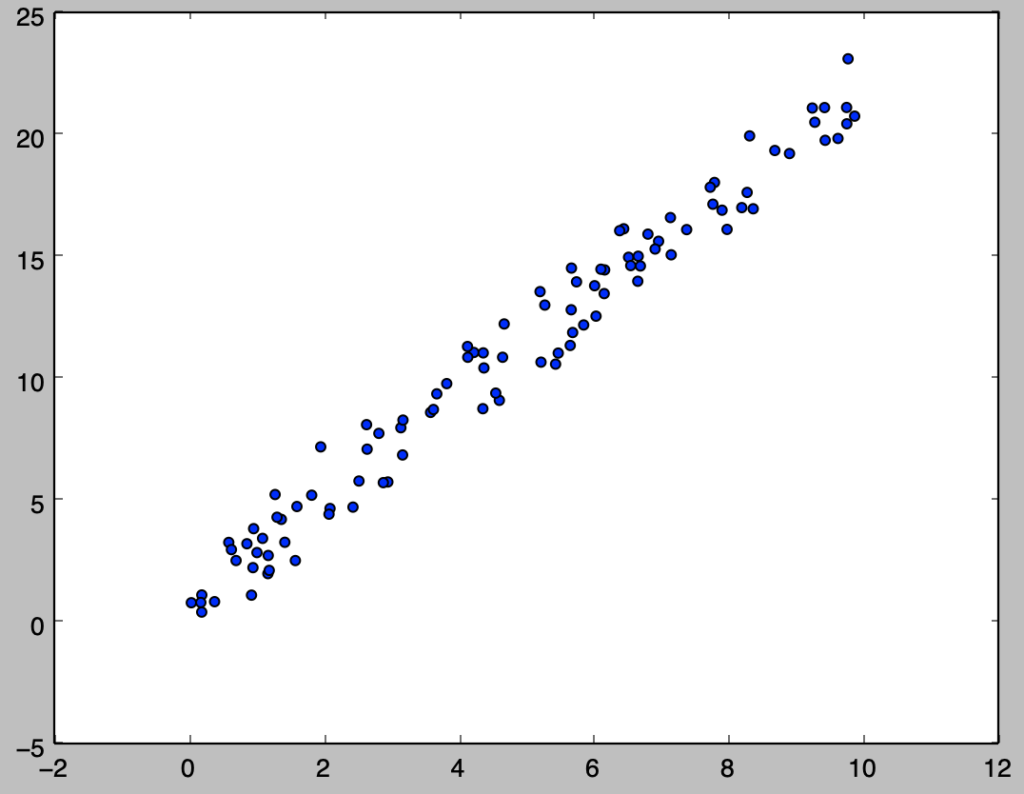
パラメータ推定
$$
\large
\begin{align}
\hat{y}_i &= \beta_0 + \beta_1 x_i \\
\hat{\beta}_1 &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2} \\
\hat{\beta}_0 &= \bar{y} – \hat{\beta}_1 \bar{x}
\end{align}
$$
前項で生成を行ったxとyに対して、上記で表した正規方程式の解に基づいて以下を実行することでパラメータ推定と回帰式の描画を行うことができる。
beta = np.zeros(2)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y) - beta[1]*np.mean(x)
print("Estimated (beta_0, beta_1): ({:.2f}, {:.2f})".format(beta[0],beta[1]))
plt.scatter(x,y,color="lightblue")
plt.plot(x,beta[0]+beta[1]*x,color="blue")
plt.show()・実行結果
> print("Estimated (beta_0, beta_1): ({:.2f}, {:.2f})".format(beta[0],beta[1]))
Estimated (beta_0, beta_1): (0.92, 2.09)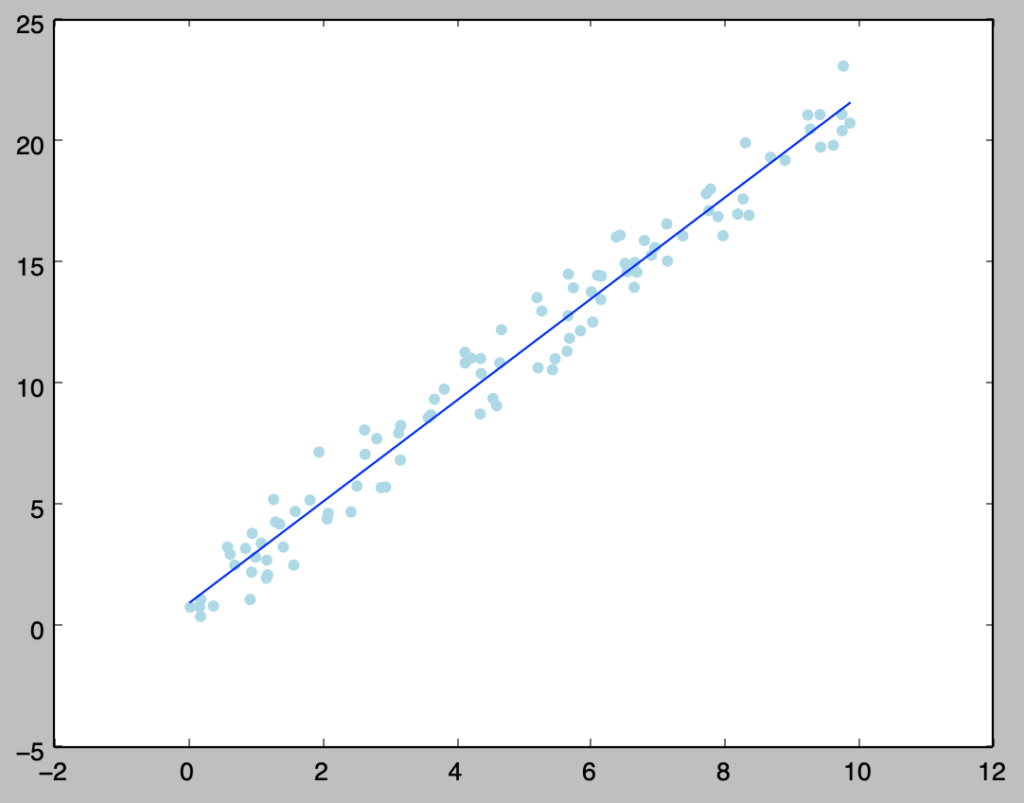
上記では$y_i = 0.7 + 2.1x_i + \epsilon_i, \quad \epsilon_i \sim N(0,1)$に対して概ね正しい結果が得られたが、切片の値がやや異なるので、サンプルを$20,000$に変えて再度パラメータ推定を行うと下記のように精度が向上することが確認できる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
beta = np.zeros(2)
x = 10*np.random.rand(20000)
y = 0.7 + 2.1*x + stats.norm.rvs(size=20000)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y) - beta[1]*np.mean(x)
print("Estimated (beta_0, beta_1): ({:.2f}, {:.2f})".format(beta[0],beta[1]))・実行結果
> print("Estimated (beta_0, beta_1): ({:.2f}, {:.2f})".format(beta[0],beta[1]))
Estimated (beta_0, beta_1): (0.70, 2.10)回帰係数の統計的推測
・仮説検定
$y_i = \beta_{0} + \beta_{1} x_i$の推定値を$\hat{\beta}_{0}, \hat{\beta}_{1}$のように定義し、回帰式の傾きに関する帰無仮説を$H_0: \hat{\beta}_{1}=a$と設定すると、このときの検定統計量$t$は下記のように計算できる。
$$
\large
\begin{align}
t &= \frac{\hat{\beta}_1-a}{s.e.(\hat{\beta}_1)} \\
s.e.(\hat{\beta}_1) &= \frac{\sqrt{\sum_{i=1}^{n} \hat{\epsilon}_{i}^{2}/n-2}}{\sqrt{\sum_{i=1}^{n} (x_i-\bar{x})^2}}
\end{align}
$$
上記の検定統計量$t$は、サンプル数が$n$のとき自由度$n-2$の$t$分布$t(n-2)$に従う。ここでは前項の例に対し、$a=1.8, 2.02, 2.1, 2.15, 2.2$とおくとき帰無仮説が棄却されるか採択されるかをそれぞれ確認する。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
a = np.array([1.8, 2.02, 2.1, 2.15, 2.2])
beta = np.zeros(2)
x = 10*np.random.rand(100)
y = 0.7 + 2.1*x + stats.norm.rvs(size=100)
beta[1] = np.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)
beta[0] = np.mean(y) - beta[1]*np.mean(x)
epsilon = y-(beta[0]+beta[1]*x)
s = np.sqrt(np.sum(epsilon**2)/(x.shape[0]-2.))
s_beta1 = s/np.sqrt(np.sum((x-np.mean(x))**2))
t = (beta[1]-a)/s_beta1
print("Estimated (beta_0, beta_1): ({:.2f}, {:.2f})".format(beta[0],beta[1]))
print("95% t-Limit: ({:.2f}, {:.2f})".format(stats.t.ppf(0.025,x.shape[0]-2),stats.t.ppf(0.975,x.shape[0]-2)))
for i in range(t.shape[0]):
if t[i] < stats.t.ppf(0.025,x.shape[0]-2) or stats.t.ppf(0.975,x.shape[0]-2) < t[i]:
print("a: {}, t: {:.3f}, {} H_0".format(a[i],t[i],"reject"))
else:
print("a: {}, t: {:.3f}, {} H_0".format(a[i],t[i],"accept"))・実行結果
Estimated (beta_0, beta_1): (0.92, 2.09)
95% t-Limit: (-1.98, 1.98)
a: 1.8, t: 8.414, reject H_0
a: 2.02, t: 2.111, reject H_0
a: 2.1, t: -0.181, accept H_0
a: 2.15, t: -1.613, accept H_0
a: 2.2, t: -3.046, reject H_0詳しくは下記などでも取り扱いを行った。
https://www.hello-statisticians.com/explain-books-cat/toukeigakunyuumon-akahon/ch13_practice.html
重回帰のパラメータ推定
サンプルの生成
$y_i = 0.3 + 2.5x_{i1} + 1.8x_{i2} + \epsilon_i, \quad \epsilon_i \sim N(0,1)$に基づいてサンプルの生成を行い、散布図を描画するにあたっては、以下を実行すれば良い。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x = 10*np.random.rand(500,3)
x[:,0] = 1.
y = 0.7 + 2.5*x[:,1] + 1.8*x[:,2] + stats.norm.rvs(size=500)
plt.subplot(1,2,1)
plt.scatter(x[:,1],y)
plt.subplot(1,2,2)
plt.scatter(x[:,2],y)
plt.show()・実行結果
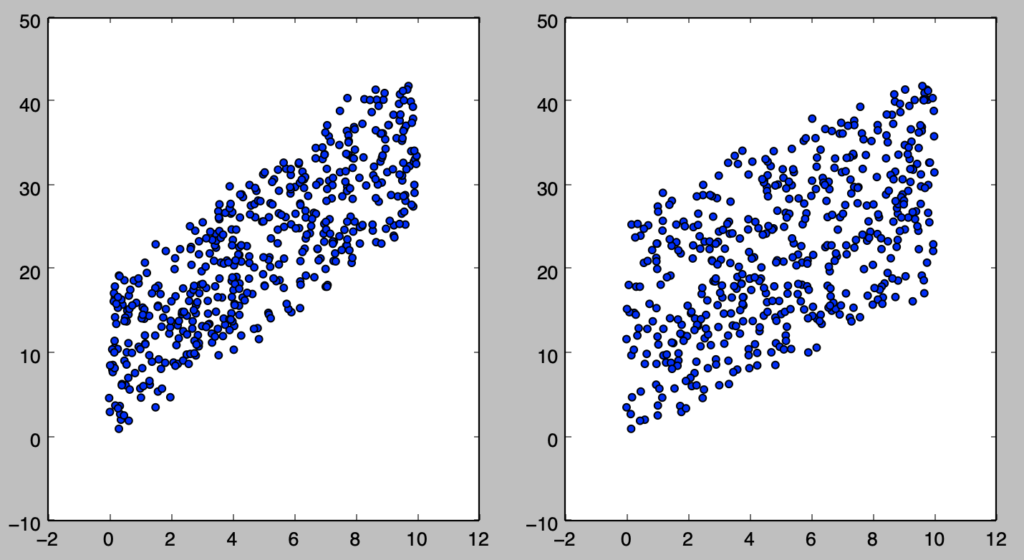
なお、xがデザイン行列になるように左の列の各行に対して、それぞれ1.の代入を行った。
パラメータ推定
$$
\large
\begin{align}
\hat{\mathbf{y}} &= \mathbf{X} \mathbf{\beta} \\
\hat{\mathbf{\beta}} &= (\mathbf{X}^{T}\mathbf{X})^{-1} \mathbf{X}^{T} \mathbf{y}
\end{align}
$$
前項で生成を行ったxとyに対して、上記で表した正規方程式の解に基づいて以下を実行することでパラメータ推定を行うことができる。
beta = np.dot(np.linalg.inv(np.dot(x.T,x)), np.dot(x.T,y))
print("Estimated (beta_0, beta_1, beta_2): ({:.1f}, {:.2f}, {:.2f})".format(beta[0], beta[1], beta[2]))・実行結果
> print("Estimated (beta_0, beta_1, beta_2): ({:.1f}, {:.2f}, {:.2f})".format(beta[0], beta[1], beta[2]))
Estimated (beta_0, beta_1, beta_2): (0.7, 2.51, 1.81)質的回帰
ロジスティック回帰
パラメータ推定
観測値$(x_i,y_i)$に対してロジスティック回帰を用いるとき、対数尤度関数は下記のように表すことができる。
$$
\large
\begin{align}
\log{L(\beta_0,\beta_1)} &= \sum_{i=1}^{n} \left( y_i \log{p_i} + (1-y_i) \log{(1-p_i)} \right) \\
&= \sum_{i=1}^{n} \left( y_i \log \left( \frac{\exp(\beta_0+\beta_1x_i)}{1+\exp(\beta_0+\beta_1x_i)} \right) + (1-y_i) \log{ \left( \frac{1}{1+\exp(\beta_0+\beta_1x_i)} \right) } \right)
\end{align}
$$
ここで上記を$\beta_0,\beta_1$に関して偏微分を行うとそれぞれ下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_0} &= \sum_{i=1}^{n} (y_i – p_i) \\
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_1} &= \sum_{i=1}^{n} (y_i – p_i) x_i \\
p_i &= \frac{\exp(\beta_0+\beta_1x_i)}{1+\exp(\beta_0+\beta_1x_i)}
\end{align}
$$
上記の式を$\beta_0,\beta_1$に関して解くのは難しいので、勾配法やニュートン法などを用いることでパラメータ推定を行う。以下では$\beta_0=1,\beta_1=1$を初期値に設定し、勾配法を用いてパラメータ推定を行う。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x = np.linspace(-3.,3.,100)
y = x + 1.5*stats.norm.rvs(size=100)
y[y>=0] = 1.
y[y<0] = 0.
alpha = 0.02
beta = np.array([1., 1.])
for i in range(50):
p = 1./(1.+np.exp(-(beta[0]+beta[1]*x)))
beta[0] += alpha*np.sum(y-p)
beta[1] += alpha*np.sum((y-p)*x)
if (i+1)%10==0:
print("Step.{}, (beta_0,beta_1): ({:2f}, {:.2f})".format(i+1,beta[0],beta[1]))
plt.scatter(x,y,color="lightgreen")
plt.plot(x,p,color="green")
plt.show()・実行結果
Step.10, (beta_0,beta_1): (0.148453, 0.97)
Step.20, (beta_0,beta_1): (-0.024882, 0.94)
Step.30, (beta_0,beta_1): (-0.056919, 0.94)
Step.40, (beta_0,beta_1): (-0.062806, 0.94)
Step.50, (beta_0,beta_1): (-0.063890, 0.94)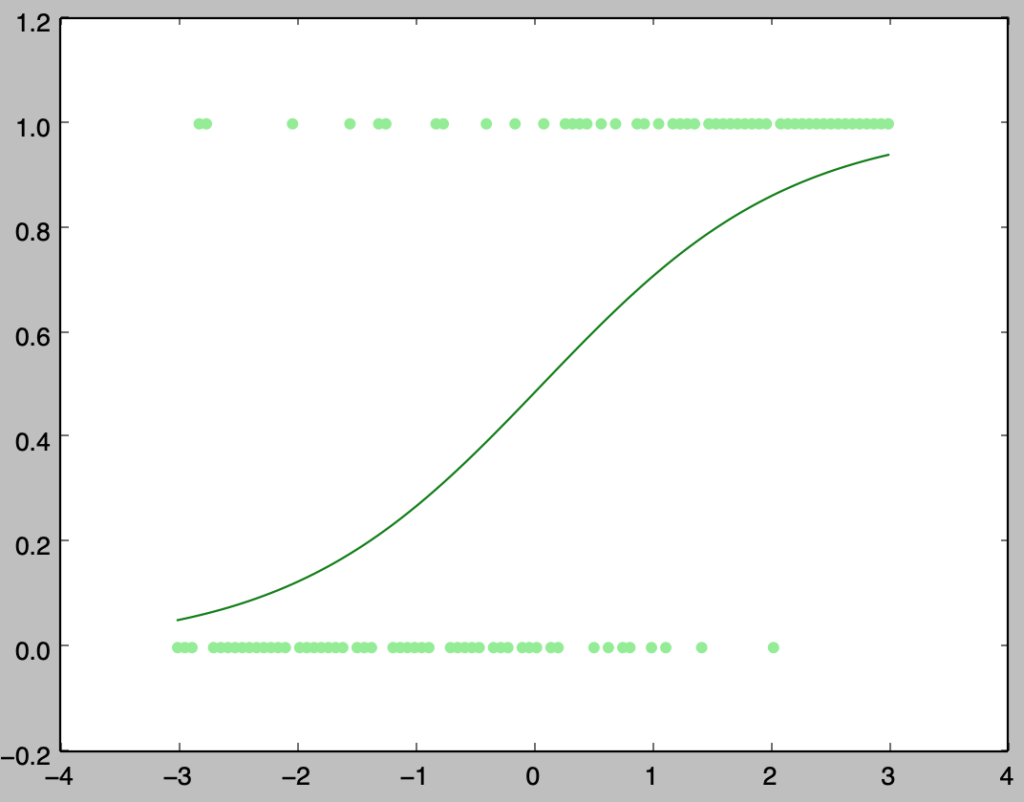
上記のように勾配法を用いることでロジスティック回帰のパラメータの推定を行うことができる。
・勾配の導出の詳細
ロジスティック回帰の対数尤度の導出
合成関数の微分とロジスティック回帰のパラメータ推定
オッズ比の計算
プロビット回帰
パラメータ推定
標準正規分布の確率密度関数を$\varphi(x)$、累積分布関数を$\Phi(x)$とおく。観測値$(x_i,y_i)$に対してプロビット回帰を用いるとき、対数尤度関数は下記のように表すことができる。
$$
\large
\begin{align}
\log{L(\beta_0,\beta_1)} = \sum_{i=1}^{n} \left( y_i \log{\Phi(\beta_0 + \beta_1 x_i)} + (1-y_i) \log{(1-\Phi(\beta_0 + \beta_1 x_i))} \right)
\end{align}
$$
ここで上記を$\beta_0,\beta_1$に関して偏微分を行うとそれぞれ下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_0} &= \sum_{i=1}^{n} \left( \frac{y_i \varphi(\beta_0+\beta_1x_i)}{\Phi(\beta_0+\beta_1x_i)} – \frac{(1-y_i) \varphi(\beta_0+\beta_1x_i)}{1-\Phi(\beta_0+\beta_1x_i)} \right) \\
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_1} &= \sum_{i=1}^{n} \left( \frac{y_i \varphi(\beta_0+\beta_1x_i)}{\Phi(\beta_0+\beta_1x_i)} – \frac{(1-y_i) \varphi(\beta_0+\beta_1x_i)}{1-\Phi(\beta_0+\beta_1x_i)} \right)x_i
\end{align}
$$
上記の式を$\beta_0,\beta_1$に関して解くのは難しいので、勾配法やニュートン法などを用いることでパラメータ推定を行う。以下では$\beta_0=1,\beta_1=1$を初期値に設定し、勾配法を用いてパラメータ推定を行う。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x = np.linspace(-3.,3.,100)
y = x + 1.5*stats.norm.rvs(size=100)
y[y>=0] = 1.
y[y<0] = 0.
alpha = 0.02
beta = np.array([1., 1.])
for i in range(50):
linear_pred = beta[0]+beta[1]*x
lp_pdf, lp_cdf = stats.norm.pdf(linear_pred), stats.norm.cdf(linear_pred)
beta[0] += alpha*np.sum(y*lp_pdf/lp_cdf - (1-y)*lp_pdf/(1-lp_cdf))
beta[1] += alpha*np.sum((y*lp_pdf/lp_cdf - (1-y)*lp_pdf/(1-lp_cdf))*x)
if (i+1)%10==0:
print("Step.{}, (beta_0,beta_1): ({:2f}, {:.2f})".format(i+1,beta[0],beta[1]))
plt.scatter(x,y,color="lightgreen")
plt.plot(x,lp_cdf,color="green")
plt.show()・実行結果
Step.10, (beta_0,beta_1): (-0.015828, 0.64)
Step.20, (beta_0,beta_1): (-0.025181, 0.90)
Step.30, (beta_0,beta_1): (-0.028015, 0.97)
Step.40, (beta_0,beta_1): (-0.028060, 0.97)
Step.50, (beta_0,beta_1): (-0.028060, 0.97)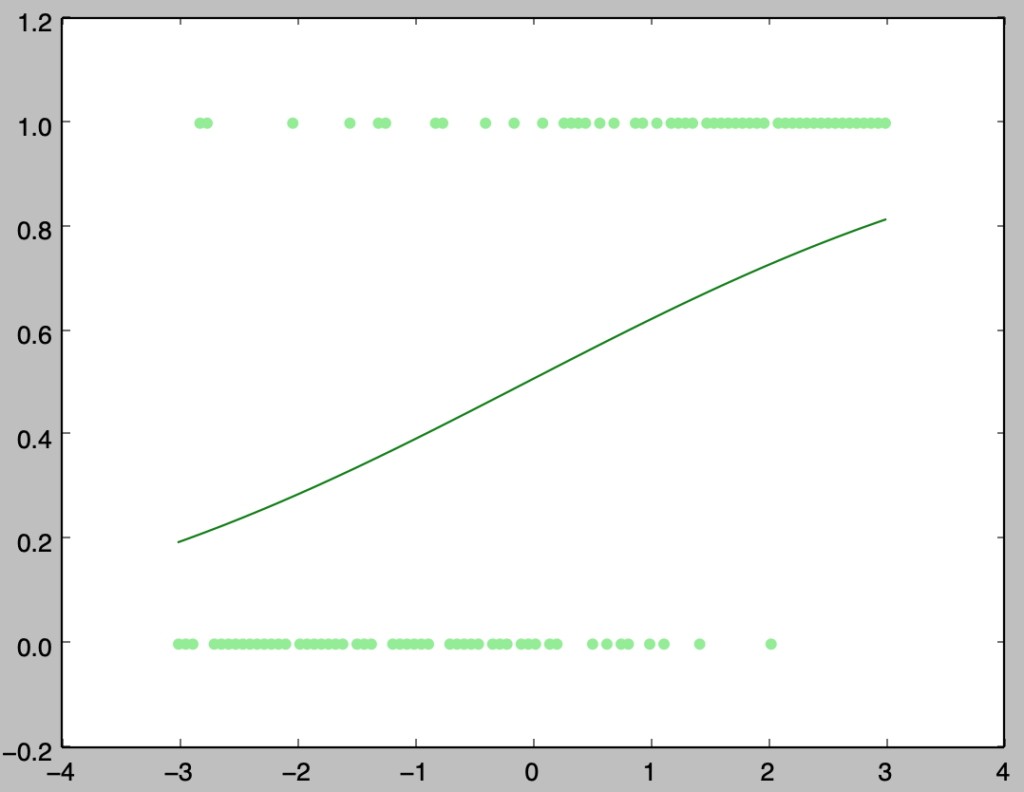
離散値の回帰
ポアソン回帰
観測値$(x_i,y_i)$に対してポアソン回帰を用いるとき、対数尤度関数は下記のように表すことができる。
$$
\large
\begin{align}
\log{L(\beta_0,\beta_1)} &= \sum_{i=1}^{n} ( y_i \log{\lambda_i} – \lambda_i – \log{y_i!} ) \\
\log{\lambda_i} &= \beta_0 + \beta_1 x_i
\end{align}
$$
ここで上記を$\beta_0,\beta_1$に関して偏微分を行うとそれぞれ下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_0} &= \sum_{i=1}^{n} \left( y_i – \exp(\beta_0+\beta_1x_i) \right) \\
\frac{\partial \log{L(\beta_0,\beta_1)}}{\partial \beta_1} &= \sum_{i=1}^{n} \left( y_i – \exp(\beta_0+\beta_1x_i) \right) x_i
\end{align}
$$
上記の式を$\beta_0,\beta_1$に関して解くのは難しいので、勾配法やニュートン法などを用いることでパラメータ推定を行う。以下では$\beta_0=0,\beta_1=0$を初期値に設定し、勾配法を用いてパラメータ推定を行う。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
pop_beta = np.array([0.5, 0.8])
x = np.linspace(-3.,3.,100)
y = stats.poisson.rvs(np.exp(pop_beta[0]+pop_beta[1]*x))
alpha = 0.001
beta = np.array([0., 0.])
for i in range(100):
grad_ = y-np.exp(beta[0]+beta[1]*x)
beta[0] += alpha*np.sum(grad_)
beta[1] += alpha*np.sum((grad_)*x)
if (i+1)%20==0:
print("Step.{}, (beta_0,beta_1): ({:2f}, {:.2f})".format(i+1,beta[0],beta[1]))
plt.scatter(x,y,color="lightgreen")
plt.plot(x,np.exp(beta[0]+beta[1]*x),color="green")
plt.show()・実行結果
Step.20, (beta_0,beta_1): (0.428261, 0.81)
Step.40, (beta_0,beta_1): (0.442874, 0.79)
Step.60, (beta_0,beta_1): (0.445618, 0.79)
Step.80, (beta_0,beta_1): (0.446100, 0.79)
Step.100, (beta_0,beta_1): (0.446182, 0.79)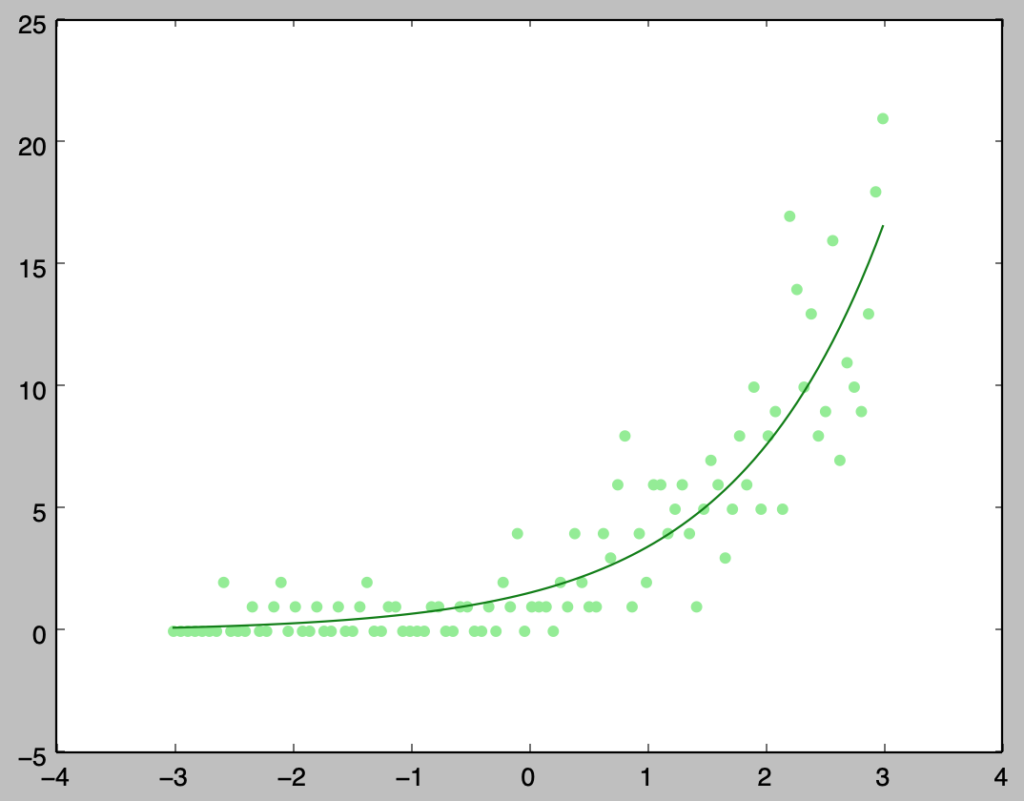
上記のように勾配法を用いることで概ね正しいパラメータを推定できることが確認できる。
・勾配の導出の詳細
ポアソン回帰の対数尤度と勾配の導出

[…] ・解説下記でPythonを用いた具体的なプログラミングを取り扱ったので、合わせて確認するとわかりやすいと思います。Pythonを用いたポアソン回帰のプログラミング […]