過去問
過去問題は統計検定公式が問題と解答例を公開しています。こちらを参照してください。
[1] 解答
$\boxed{\mathsf{3}}$ : $③$
$n$ 人からの回答をそれぞれ $X_1, X_2, \dots, X_n$ とする.帰無仮説 $p = 0.4$ の下で,$\displaystyle{\sum_{i = 1}^n X_i}$ は二項分布 $B(n,p) = B(600,0.4)$ に従う.$n=600$ は十分大きいので,$B(600,0.4)$ は正規分布 $N(600 \times 0.4, 600 \times 0.4 \times 0.6$) で近似できる.よって $\dfrac{\sum_{i=1}^{600} X_i}{600} \sim N\left(0.4, \dfrac{0.4 \times 0.6}{600}\right)$ となる.標本支持率 $\hat{p}$ は,$\hat{p} = \dfrac{\sum_{i=1}^{600} X_i}{600}$ であるから,$\hat{p} \sim N\left(0.4, \dfrac{0.4 \times 0.6}{600}\right)$となる.したがって, $\dfrac{\hat{p}- 0.4}{\sqrt{0.4 \times 0.6/600}}$ は標準正規分布 $N(0,1)$ に従う.
標準正規分布の $5\%$ 点は $1.645$ であるから,
$$
P\left( \dfrac{\hat{p}- 0.4}{\sqrt{0.4 \times 0./600}} \geq 1.645 \right) = 0.95
$$
となる.したがって,
$$
\begin{align*}
\dfrac{\hat{p}-0.4}{\sqrt{0.4 \times 0.6/600}} &\geq 1.645 \\
\hat{p} &\geq 1.645 \times \sqrt{0.4 \times 0.6/600} + 0.4 \\
&\approx 0.4329 \\
\end{align*}
$$
となる.
[2] 解答
$\boxed{ \mathsf{4} }$ : ⑤
第二種の過誤の確率を $\beta$ とすると,検出力は $1-\beta$ である.第二種の過誤の確率とは,対立仮説の下で有意と判定されない確率のことであるから,$H_1:p= 0.45$の下で,$P(\hat{p} \geq c)$を求めれば良い.(ただし,$[1]$ で求めた $c = 0.433$ を利用する )
$[1]$ と同様に $\dfrac{\hat{p}-0.45}{\sqrt{0.45 \times 0.55/600}} \sim N(0,1)$ であり,また,
$$
\dfrac{\hat{p} – 0.45}{\sqrt{0.45 \times 0.55/600}} \geq \dfrac{c-0.45}{\sqrt{0.45 \times 0.55/600}} = \dfrac{0.433-0.45}{\sqrt{0.45 \times 0.55/600}} \approx -0.84
$$
であるから,
$$
\hat{p} \geq c \Leftrightarrow \dfrac{\hat{p} – 0.45}{\sqrt{0.45 \times 0.55/600}} \geq -0.84.
$$
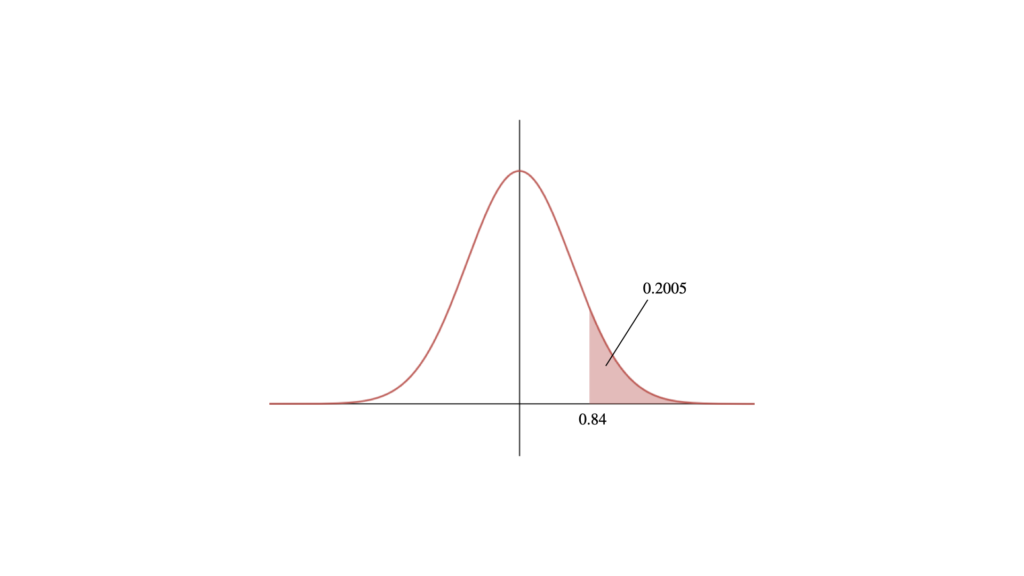
ここで標準正規分布表から $0.84$ に対する上側確率は $0.2005$ であるから,
$$
P\left( \dfrac{\hat{p} – 0.45}{\sqrt{0.45 \times 0.55/600}} \geq -0.84 \right) = 1-0.2005 = 0.7995
$$
となる.
[3] 解答
$\boxed{ \mathsf{4} }$ : ⑤
$H_0$ の下での支持率を $p_0=0.4$ ,$H_1$ の下での支持率を $p_1=0.45$ とする.
$H_0$ の下で,$P(\hat{p} \geq c) = 0.05$ かつ $H_1$ の下で,$P(\hat{p} \geq c) = 0.95$ となるような必要最低限のサンプルサイズ $n$ を求める.
$H_0$ の下で $\dfrac{\hat{p}-p_0}{\sqrt{p_0(1-p_0)/n}} \sim N(0,1)$であるから,このとき
$$
\begin{align}
\dfrac{\hat{p}-p_0}{\sqrt{p_0(1-p_0)/n}} \geq 1.645
\end{align}
$$
また,$H_1$ の下でも同様に,$\dfrac{\hat{p}-p_1}{\sqrt{p_1(1-p_1)/n}} \sim N(0,1)$ であるから,
$$
\begin{align}
\dfrac{\hat{p}-p_0}{\sqrt{p_1(1-p_1)/n}} \geq -1.645
\end{align}
$$ である.
これら $2$ つの不等式の左辺は $n$ について単調増加であるから.両式の不等号を等号に置き換えた連立方程式を解けば条件を満たすために最低限必要なサンプルサイズ $n$ が求まる.
$$
\left\{
\begin{align}
&\dfrac{\hat{p}-0.40}{\sqrt{0.40\cdot 0.60/n}} = 1.645 \\
&\dfrac{\hat{p}-0.45}{\sqrt{0.45\cdot0.55/n}} = -1.645
\end{align}
\right.
$$
この $2$ 式から $\hat{p}$ を消去すると,
$$
\begin{align*}
\sqrt{n} &= \dfrac{1.645(\sqrt{0.45\cdot 0.55}) + \sqrt{0.40 \cdot 0.60})}{0.45-0.40} \\
&= 32.48
\end{align*}
$$
したがって,$n\approx 1055$ .
