過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定2級(2018.11)【問題】(統計検定公式)<※期間限定>
- 統計検定2級(2018.11)【正解】(統計検定公式)
問1 解答
(比率,箱ひげ図)
[1]
$\boxed{ \ \mathsf{1}\ }$ ⑤
相対度数=各階級の度数の割合 $(r_i=f_i/N)$なので,全階級の相対度数の合計は $1=100\%$
(ア) $100.0-85.1-2.1=12.8$
(イ) $100.0-76.6-17.0-2.1=4.3$
[2]
$\boxed{ \ \mathsf{2}\ }$ ①
各箱ひげ図の最大値の値(外れ値になっている)をみると,Aが70ぐらい,Bが100ぐらい,Cが140ぐらいとなっているので,相対度数分布表から各年の最も高い階級を見ると,Aが1952年,Bが1985年,Cが2017年となる。
[3]
$\boxed{ \ \mathsf{3}\ }$ ③
Ⅰ.箱ひげ図から箱の高さを比較すると四分位範囲は大きい(縦軸のスケールに注意)。誤り。
Ⅱ.A(1952年)の最大値が70強に対し,B(1985年)の最大値が100強程度なので,半分以下ではない。誤り。
Ⅲ.箱ひげ図から中央値の値を比較すれば明らか。正しい。
問2 解答
(相関係数)
$\boxed{ \ \mathsf{4}\ }$ ①
Ⅰ.20~54歳までの値を見ると強い相関が見受けられるので,相関係数が低いというだけで関係性が強くないと判断できない。正しい。
Ⅱ.20~54歳までの値を見ると相関が強くなるので,相関係数の値は大きくなる。誤り。
Ⅲ.相関係数からはこのような関係はわからない(回帰係数でわかる)。誤り。
問3 解答
(価格指数,変化率)
[1]
$\boxed{ \ \mathsf{5}\ }$ ①
前月比の変化率 $=($当月値$)/($前月値$)-1$
$\therefore\ \ 117.7/($ア$)-1=4.98\%\ \ \Rightarrow\ \ ($ア$)=106.40$
[2]
$\boxed{ \ \mathsf{6}\ }$ ④
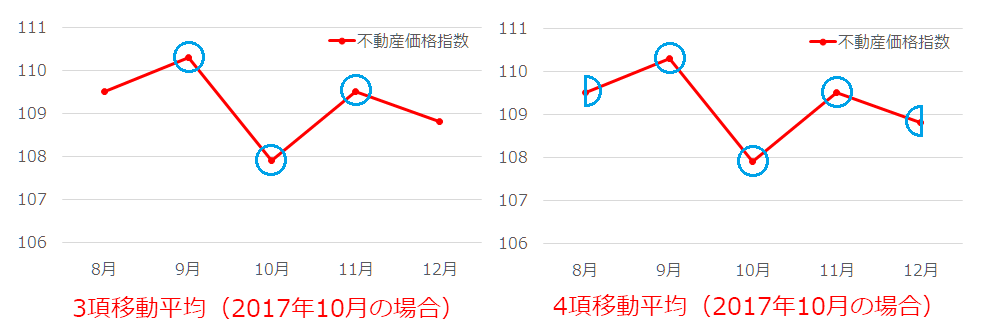
3項移動平均は,当期値に1期前値と1期後値との3つの平均をとったもの。
※4項移動平均のように偶数項の移動平均は両端の値は $1/2$ をかけて平均をとる。
4項移動平均 $\displaystyle\frac{109.5/2+110.3+107.9+109.5+108.8/2}4$
問4 解答
(価格指数)
$\boxed{ \ \mathsf{7}\ }$ ②
ラスパイレス物価指数…基準年の購入量や取引量等を重みとして算出した価格指数。
品目$i$の基準年価格$=p_{oi}$,基準年数量$=q_{oi}$,比較年価格$=p_{ti}$として$$P_L=\frac{\sum_ip_{ti}q_{0i}}{\sum_ip_{0i}q_{0i}}$$
※他の物価指数
パーシェ物価指数…比較年の購入量や取引量等を重みとして算出した価格指数。
品目$i$の基準年価格$=p_{oi}$,比較年数量$=q_{ti}$,比較年価格$=p_{ti}$として$$P_P=\frac{\sum_ip_{ti}q_{ti}}{\sum_ip_{0i}q_{ti}}$$
フィッシャー物価指数…ラスパイレス指数とパーシェ指数の幾何平均で求められる価格指数。$$P_F=\sqrt{P_L\times P_P}$$
問5 解答
(標本抽出法(無作為抽出))
$\boxed{ \ \mathsf{8}\ }$ ③
単純無作為抽出法・・・母集団の中から無作為に標本を抽出する方法。
層化無作為抽出法・・・母集団をあらかじめいくつかの層(グループ)に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法。
(通常,層の大きさに比例させて調査対象を抽出する大きさを決める。(比例配分法))
Ⅰ.単純無作為抽出法では,全部で$N$個の個体からなる母集団から$n$個の標本を得るとき,各個体が選択される確率は等しく$n/N$,どの個体の組も選択される確率が等しく${}_NC_n$。正しい。
Ⅱ.層化無作為抽出法において,分割した層内の分散はできるだけ小さくなるようにするが,これによって母集団平均の推定値の分散が小さくなることはない。誤り。
Ⅲ.母集団がいくつかの層に分けられた場合,単純無作為抽出法では,母集団内からランダムに標本を抽出するので,場合によってはある特定の層を全く含まない可能性がありうる。正しい。
問6 解答
(標本抽出法)
$\boxed{ \ \mathsf{9}\ }$ ②
集落(クラスター)抽出法・・・母集団を小集団であるクラスター(集落)に分け,その中からいくつかのクラスターを無作為に抽出し,それぞれのクラスターにおいて全数調査を行う。
二段抽出法・・・母集団をいくつかのグループ(第1段抽出)に分け,その中からいくつかグループを無作為に抽出し,さらにそこから標本を無作為に抽出(第2段抽出)する。
系統抽出法・・・通し番号をつけた名簿を作成し,1番目の調査対象を無作為に選び、2番目以降の調査対象を一定の間隔で抽出する方法。
問7 解答
(条件付き確率,ベイズの定理)
[1]
$\boxed{ \ \mathsf{10}\ }$ ②
カモノハシがプリントされているクッキーは,
全体の $70\%$ を占めるA工場分には $2\%$,
全体の $30\%$ を占めるB工場分には $8\%$,
含まれているので,全体に占めるカモノハシのクッキーの割合は$$70\%\times2\%+30\%\times8\%=0.7\times0.02+0.3\times0.08=0.038$$
[2]
$\boxed{ \ \mathsf{11}\ }$ ②
工場Aで生産されたという事象を $A$,カモノハシがプリントされているという事象を$B$とすると,
$$P(A)=0.7,\ P(B|A)=0.02,\ P(B)=0.038$$
となるので,無作為に抽出したクッキーにカモノハシがプリントされていたとき,それが工場Aで製造されているという確率(事象 $B$ が起こったという条件下で事象 $A$ が起こる確率)は,
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{0.02\times0.7}{0.038}=0.3684$$
※このとき,$P(A)$ を事前確率,$P(A|B)$ を事後確率,$P(B|A)$ を尤度という。
問8 解答
(確率変数の和と差)
[1]
$\boxed{ \ \mathsf{12}\ }$ ④
$$P(Y\ge0)=P(0.3+2x+U\ge0)=P(U\ge-0.3-2x)=0.95\\$$
$U\sim N(0,1)$なので,
$P(U\ge a)=P(-U\le -a)=1-P(-U\ge -a)$ ($U$ は $x=0$ に対して対称)
$$P(-U\ge0.3+2x)=1-0.95=0.05\\$$標準正規分布表から$$0.3+2x=1.645\ \ \Rightarrow\ \ x=(1.645-0.3)/2=0.6725$$
[2]
$\boxed{ \ \mathsf{13}\ }$ ①
$Y$ は $U$ と単調増加の関係になる。よって,$U$ の上側 $5\%$ 点を $u=1.645$ とすると,$Y$ の上側 $5\%$ 点 $y$ は $$y=0.3+2x+u=0.3+2x+1.645=2x+1.945$$グラフは傾き $2$ の直線となる。
問9 解答
(二項分布)
[1]
$\boxed{ \ \mathsf{14}\ }$ ②
$X$ は成功確率 $p=2/6=1/3$ の試行を $n=7$ 回行って成功する回数の分布なので,二項分布 $B(n,p)=B(7,1/3)$ に従う。$$\begin{align}P(X=x)=&{}_7\mathrm{C}_x(1/3)^x(1-1/3)^{7-x}\\P(X=x+1)=&{}_7\mathrm{C}_{x+1}(1/3)^{x+1}(1-1/3)^{6-x}\\\therefore\ \frac{P(X=x+1)}{P(X=x)}=&\frac{{}_7\mathrm{C}_{x+1}(1/3)^{x+1}(1-1/3)^{6-x}}{{}_7\mathrm{C}_x(1/3)^x(1-1/3)^{7-x}}\\=&\frac{(7-x)(1/3)}{(x+1)(1-1/3)}=\frac{-x+7}{2x+2}\end{align}$$
[2]
$\boxed{ \ \mathsf{15}\ }$ ②
[1]の結果から$$P(X=x+1)>P(X=x)\ \ \Leftrightarrow\ \ \frac{P(X=x+1)}{P(X=x)}>1\ \ \Leftrightarrow\ \ \frac{-x+7}{2x+2}>1\ \ \Leftrightarrow\ \ x<5/3$$同様に$$P(X=x+1)<P(X=x)\ \ \Leftrightarrow\ \ x>5/3$$よって,$P(X=0)<P(X=1)<P(X=2)>P(X=3)>P(X=4)\cdots$
問10 解答
(標本平均の期待値,分散)
$\boxed{ \ \mathsf{16}\ }$ ③
$X_1,\dots,X_n$は互いに独立で,期待値が $\mu$,分散が $\sigma^2$ なので,$$E[X_i]=\mu,V[X_i]=\sigma^2,\mathrm{Cov}[X_i,X_j]=0\ \ (i\ne j)$$よって,$$\begin{align}E[\bar X]=&E\left[\frac1n\sum_{i=1}^nX_i\right]=\frac1n\sum_{i=1}^nE\left[X_i\right]=\frac1n\times n\mu=\mu\\V[\bar X]=&V\left[\frac1n\sum_{i=1}^nX_i\right]\\=&\frac1{n^2}V\left[\sum_{i=1}^nX_i\right]\\=&\frac1{n^2}\left(\sum_{i=1}^nV\left[X_i\right]+\sum_{i\ne j}\mathrm{Cov}\left[X_i,X_j\right]\right)\\=&\frac1{n^2}\times n\sigma^2=\frac{\sigma^2}{n}\end{align}$$
