過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定2級(2016.06)【正解】(統計検定公式)
問8 解答
(連続型確率変数,確率変数の分散)
[1]
$\boxed{ \ \mathsf{19}\ }$ ④
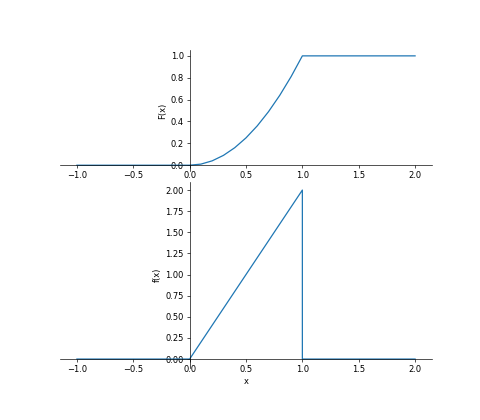
中央値を $c$ とすると,$\displaystyle F(c)=\frac12\ (0\le c\le 1)$。よって
$$c^2=\frac12\ \ \Rightarrow\ \ c=\sqrt{\frac12}\fallingdotseq0.707$$
[2]
$\boxed{ \ \mathsf{20}\ }$ ②
確率変数 $X$ の確率密度関数は,分布関数を微分して求める。
$$\begin{eqnarray}f(x)=\begin{cases}2x&:&0\le x\le1\\0&:&other\end{cases}\end{eqnarray}$$よって
$$\begin{align}
E[X]=&\int_0^1xf(x)dx=\int_0^12x^2dx=\left[\frac23x^3\right]_0^1=\frac23\\
E[X^2]=&\int_0^1x^2f(x)dx=\int_0^12x^3dx=\left[\frac12x^4\right]_0^1=\frac12\\
V[X]=&E[X^2]-E[X]^2=\frac12-\left(\frac23\right)^2=\frac1{18}\fallingdotseq0.056\
\end{align}$$
問9 解答
(標本サイズ)
[1]
$\boxed{ \ \mathsf{21}\ }$ ①
母集団から抽出した標本 $X_1,\dots,X_n$ の標本平均 $\bar X$ の平均,分散は$$\begin{align}
E\left[\bar X\right]=&E\left[\frac1n\sum_iX_i\right]=\frac1n\sum_iE\left[X_i\right]=\frac1n\times n\mu=\mu\\
V\left[\bar X\right]=&V\left[\frac1n\sum_iX_i\right]=\frac1{n^2}\sum_iV\left[X_i\right]=\frac1{n^2}\times n\sigma^2=\frac{\sigma^2}{n}
\end{align}$$となる。よって推定量の変動係数は $\displaystyle\frac{\sqrt{\sigma^2/n}}{\mu}$
[2]
$\boxed{ \ \mathsf{22}\ }$ ②
母集団での変動係数が $0.8$ 以下なので,$$\frac{\sigma}{\mu}\le0.8$$推定量の変動係数 $0.05$ 以下に抑えるためには$$\frac{\sqrt{\sigma^2/n}}{\mu}\le0.05\ \ \Rightarrow\ \ \sqrt{n}\ge\frac1{0.05}\frac{\sigma}{\mu}\ge\frac1{0.05}\times0.8=16$$よって,$n\ge16^2=256$。
問10 解答
(二項分布,一致性,不偏性,推定量と推定値)
[1]
$\boxed{ \ \mathsf{23}\ }$ ⑤
無作為に抽出した有権者に質問して市長か新人かの二択で回答する。同じ有権者に質問しないので,抽出は非復元抽出であるが,母集団にあたる投票した全有権者数が十分大きいために,復元抽出とみなすことができる。
復元抽出で2択の一方に回答(ベルヌーイ試行)した有権者数が従う分布は二項分布となる。
[2]
$\boxed{ \ \mathsf{24}\ }$ ②
$x_1,\dots,x_n\ (x_i\in{0,\ 1})$ を無作為標本としたとき,標本平均 $\displaystyle\bar x=\frac1n\sum_ix_i$ は,$n$ が十分大きいとき $\bar x$ は明らかに母集団の平均 $\mu$ に近づくので,一致推定量である。
また,$\displaystyle E\left[\bar x\right]=\frac1n\sum_iE[x_i]=\mu$となるので不偏推定量でもある。
[3]
$\boxed{ \ \mathsf{25}\ }$ ⑤
$X_i$ が二項分布 $N(n,p)$ に従うとすると,平均は $E[X_i]=np$,分散は $V[X_i]=np(1-p)$ となる。
そこで,標本平均の分散は$$V[\bar X]=V\left[\frac1n\sum_iX_i\right]=\frac1{n^2}\sum_iV\left[X_i\right]=\frac{p(1-p)}{n}$$ここで,$p=0.45,\ n=2000$ を代入すると$$V[\bar X]=\frac{0.45\times0.55}{2000}$$
問11 解答
(母平均の区間推定,母平均の検定(母分散未知),母平均の差の検定)
[1]
$\boxed{ \ \mathsf{26}\ }$ ③
母分散の値が未知のとき,母分散 $\sigma^2$ の代わりに不偏分散 $s^2$ を用いた統計量$$t=\frac{\bar x-\mu}{\sqrt{s^2/n}}$$は自由度 $n-1$ の $t$ 分布 $t(n-1)$ に従う。区間推定のためには,上側確率が $\alpha/2$ となる値 $t_{\alpha/2}(n-1)$ を求めると,$$P(|t|\le t_{\alpha/2}(n-1))=1-\alpha$$
となるので,母平均の $100(1-\alpha)\%$ 信頼区間は$$\begin{eqnarray}&\left|\frac{\bar x-\mu}{\sqrt{s^2/n}}\right|\le t_{\alpha/2}(n-1)\\&\therefore\ \bar x-t_{\alpha/2}(n-1)\sqrt{s^2/n}\le\mu\le\bar x+t_{\alpha/2}(n-1)\sqrt{s^2/n}\end{eqnarray}$$これから,母比率の$99\%$信頼区間は,$\bar x=1.01$,$n=6$,$s^2=0.11^2$,$\alpha=0.01$ として $t_{0.005}(5)=4.032$ なので,$$\begin{eqnarray}&1.01-4.032\sqrt{0.11^2/6}\le\mu\le1.01+4.032\sqrt{0.11^2/6}\\&0.83\le\mu\le1.19\end{eqnarray}$$
[2]
$\boxed{ \ \mathsf{27}\ }$ ⑤
帰無仮説 $H_0:\mu=1$,対立仮説 $H_1:\mu\ne1$ の下で統計検定量は$$t=\frac{\bar x-\mu}{\sqrt{s^2/n}}=\frac{1.01-1}{\sqrt{0.11^2/6}}=0.223$$一方,$t$ 分布表から,自由度 $5$ の $t$ 分布の上側 $10\%$ 点は $t_{0.1}(5)=1.476$であり,上の統計検定量よりも大きい。したがって,両側検定なので,$P_-$ 値は $10\%=0.1$ の2倍の $0.2$ よりも大きくなる。
[3]
$\boxed{ \ \mathsf{28}\ }$ ③
2つの母集団 $N(\mu_a,\sigma^2),N(\mu_b,\sigma^2)$からの標本 (データ数 $m,n$,標本平均 $\bar x_a,\bar x_b$,不偏分散 $s^2_a,s^2_b$ があるとき,2つの母集団の平均の差を検定する。
帰無仮説 $H_0:\mu_a=\mu_b$の下で,統計検定量$$t=\frac{\bar x_a-\bar x_b}{\sqrt{\frac1m+\frac1n}}\hat s\ \ \left(\hat s=\frac{(m-1)s^2_a+(n-1)s^2_b}{m-n-2}\right)$$は,自由度 $m-n-2$ の $t$ 分布に従う。
問12 解答
(検出力)
$\boxed{ \ \mathsf{29}\ }$ ④
| 真実 | |||
| 帰無仮説が正しい | 対立仮説が正しい | ||
| 検定の結果 | 帰無仮説を棄却しない (対立仮説が正しいとは言えない) | 正しい | 第二種の過誤(β) |
| 帰無仮説を棄却する (対立仮説が正しい) | 第一種の過誤(α) 有意水準 | 正しい 検出力(1-β) | |
対立仮説が $\mu=630$となるので,検出力はこの対立仮説が正しいときの棄却域の確率を求めればよい。$$\begin{eqnarray}&P\left(\frac{\bar X-600}{10}>2.33\right)=P\left(\frac{\bar X-630+30}{10}>2.33\right)\\&=P\left(\frac{\bar X-630}{10}>2.33-3=-0.67\right)\end{eqnarray}$$
ここで,対立仮説が正しいとき,$\displaystyle\frac{\bar X-630}{10}$ は標準正規分布に従うので,$$P\left(\frac{\bar X-630}{10}>-0.67\right)=1-P\left(\frac{\bar X-630}{10}>0.67\right)=1-0.2514=0.7486$$
問13 解答
(独立性の検定)
独立性の検定は,2つの属性$A,B$が独立かどうかの検定である。
属性$A$のカテゴリが$A_i$,属性$B$のカテゴリが$B_j$の観測度数を$f_{ij}=O_{ij}$とし,
$f_{i\cdot}=\sum_jf{ij}$を$i$行の度数合計(行和),
$f_{\cdot j}=\sum_if{ij}$を$j$列の度数合計(列和),
$f_{\cdot\cdot}=\sum_i\sum_jf_{ij}=\sum_if_{i\cdot}=\sum_jf_{\cdot j}=n$を全度数合計という。
| $B_1$ | $B_2$ | $\cdots$ | $B_c$ | 計 | |
| $A_1$ | $f_{11}$ | $f_{12}$ | $\cdots$ | $f_{1c}$ | $f_{1\cdot}$ |
| $A_2$ | $f_{21}$ | $f_{22}$ | $\cdots$ | $f_{2c}$ | $f_{2\cdot}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | |
| 計 | $f_{\cdot1}$ | $f_{\cdot2}$ | $\cdots$ | $f_{\cdot\cdot}$ |
属性$A,B$が独立という帰無仮説は,$H_0:P(A\cap B)=P(A)P(B)$が成り立つことである。
ここで,カテゴリ$A_i,B_j$の出現確率はそれぞれ$f_{i\cdot}/n,f_{\cdot j}/n$であるので,$H_0$のもとで,属性$A$のカテゴリが$A_i$,属性$B$のカテゴリが$B_j$の期待度数は
$$E_{ij}=n(f_{i\cdot}/n)(f_{\cdot j}/n)=f_{i\cdot}f_{\cdot j}/n$$
となる。
帰無仮説$H_0$の下で,次の検定統計量$\chi^2$は度数が大きいときに近似的に$\chi^2$分布に従う。行和と列和が固定されていることから自由度は$(r$(行の数)$-1)\times(c$(列の数)$-1)$となる。
$$\chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\sim\chi^2((r-1)(c-1))$$
有意水準$100\alpha\%$で帰無仮説が棄却されるには,$\chi^2$分布の上側$\alpha$点より上で求めた$\chi^2$統計量が大きくなればよい。
[1]
$\boxed{ \ \mathsf{30}\ }$ ⑤
期待度数は以下の通り。
| 購入したいと思う | 購入したいと思わない | 計 | |
| 男性 | $\frac{120\times120}{220}\fallingdotseq65.5$ | $\frac{120\times100}{220}\fallingdotseq54.5$ | $120$ |
| 女性 | $\frac{100\times120}{220}\fallingdotseq54.5$ | $\frac{100\times100}{220}\fallingdotseq45.5$ | $100$ |
| 計 | $120$ | $100$ | $220$ |
よって,帰無仮説:「2つの変数は独立である」の下で,検定統計量$\chi^2$は$$\begin{align}\chi^2=&\sum_{i=1}^r\sum_{j=1}^c\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\\=&\frac{(80-65.5)^2}{65.5}+\frac{(40-54.5)^2}{54.5}+\frac{(40-54.5)^2}{54.5}+\frac{(60-45.5)^2}{45.5}\end{align}$$
[2]
$\boxed{ \ \mathsf{31}\ }$ ①
自由度は$(2-1)\times(2-1)=1$
問14 解答
(単回帰モデル,統計ソフトウェアの活用)
※重回帰モデルの統計ソフトウェアによる出力結果の主な項目
$\mathtt{Estimate}$:回帰係数($\alpha,\beta_1,\beta_2$)の推定値
$\mathtt{Std.Error}$:回帰係数の推定値の標準誤差
$\mathtt{t\ value}$:$t$値,$\mathtt{Pr(\gt|t|)}$:$P_-$値・・・回帰係数の検定で使う
$\mathtt{Rasidual\ standard\ error}$:誤差項の標準偏差の推定値
$\mathtt{degrees\ of\ freedom}$:自由度
$\mathtt{Multiple\ R-squared}$:決定係数($R^2$)
$\mathtt{Adjusted\ R-squared}$:自由度調整済み決定係数($R^{*2}$)
$\mathtt{F-statistic}$:$F$検定統計量,$\mathtt{p-value}$:$P_-$値・・・回帰の有意性の検定で使う
[1]
$\boxed{ \ \mathsf{32}\ }$ ④
定数項を含む回帰係数の推定値 $\hat\beta_i$ について,帰無仮説 $\beta_i=0$,対立仮説 $\beta_i\ne0$ のもとで,統計検定量 $t$ 値は$$t=\frac{\hat\beta_i-\beta_i}{\mathrm{se}(\hat\beta_i)}=\frac{\hat\beta_i}{\mathrm{se}(\hat\beta_i)}$$は自由度 $n-p-1$ の $t$ 分布に従う($n$は観測数,$p$は説明変数の数)。
このとき,有意水準$100\alpha\%$で帰無仮説を棄却する棄却域は次の式で与えられる。$$|t|=\left|\frac{\hat\beta_i}{\mathrm{se}(\hat\beta_i)}\right|\ge t_{\alpha/2}(n-p-1)$$一方,$P_-$ 値は統計検定量 $t$ 値が与えられたとき,$P(X>|t|)$となる確率であり,この値が有意水準より小さければ帰無仮説は棄却され,回帰係数の有意性がいえる。
[2]
$\boxed{ \ \mathsf{33}\ }$ ⑤
平均給与は標本平均が $0$ となるように全国平均からの偏差の値を用いているため,新聞購読数の予測をするためには,回帰式に平均給与 $=0$,高齢者数 $=0.5$を代入して求める。
[3]
$\boxed{ \ \mathsf{34}\ }$ ③
① 出力結果の $F$ 値の値は,「平均給与と高齢者数の係数がともに $0$ である」という帰無仮説に関する検定統計量の値である。$P_-$ 値はこの検定量から求められるが,$P_-$ 値が有意水準より小さい場合は,$F$ 値が棄却域に含まれるため,帰無仮説が棄却される。誤り。
② 決定係数はモデルの回帰係数の当てはまり具合を表す指標(回帰による平方和が総平方和に占める割合)であって,予測の精度を表す指標ではない。誤り。
③ 高齢者数の回帰係数が約 $1.0$ であることから,高齢者数が $0.1$ 増加すると新聞購読数は $0.1\times1.0=0.1$ 増加する。正しい。
④ $P_-$ 値から,平均給与の回帰係数は有意水準 $1\%$ でも有意新聞購読数の大小に影響があるといえる。誤り。
⑤ 高齢者数の回帰係数は「回帰係数は0に等しい」という帰無仮説の下で有意水準 $5\%$ で有意であるので,回帰係数の $(100-5)\%$ 信頼区間は $0$ を含まない。誤り。
