当記事は「パターン認識と機械学習」の読解サポートにあたってChapter.$8$の「グラフィカルモデル」の章末問題の解説について行います。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。
・参考
パターン認識と機械学習 解答まとめ
https://www.hello-statisticians.com/answer_textbook#prml
解答まとめ
問題$8.2$
背理法で考える。「番号が大きなノードに対してのみエッジを持つ有向グラフ」で閉路を持つにはどれかのノードが番号がマイナスになるノードに対してエッジを持たなくてはならないが、このことは「番号が大きなノードに対してのみエッジを持つ」という前提に反する。よって閉路を持たない。
問題$8.3$
$a=1,b=1$の場合に限って示す。Table$8.2$より、$p(a,b), p(a), p(b)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
p(a,b) &= 0.048+0.096 = 0.144 \\
p(a) &= 0.192+0.064+0.048+0.096 = 0.4 \\
p(b) &= 0.048+0.216+0.048+0.096 = 0.408
\end{align}
$$
ここで$p(a)p(b) = 0.1632 \neq 0.144 = p(a,b)$より$p(a,b) \neq p(a)p(b)$である。次に$c$で条件付けた場合を考えるにあたって、$p(a,b|c), p(a|c), p(b|c)$の値を考える。
・$c=0$の場合
$p(c=0)=0.192+0.048+0.192+0.048=0.48$を用いて下記のように計算できる。
$$
\large
\begin{align}
p(a,b|c=0) &= 0.048/0.48 = 0.1 \\
p(a|c=0) &= (0.192+0.048)/0.48 = 0.5 \\
p(b|c=0) &= (0.048+0.048)/0.48 = 0.2
\end{align}
$$
よって$p(a,b|c=0) = 0.1 = 0.5 \times 0.2 = 0.1 = p(a,b|c=0)$が成立する。
・$c=1$の場合
$p(c=1)=0.144+0.216+0.064+0.096=0.52$を用いて下記のように計算できる。
$$
\large
\begin{align}
p(a,b|c=1) &= 0.096/0.52 = \frac{9.6}{52} \\
p(a|c=1) &= (0.064+0.096)/0.52 = \frac{16}{52} \\
p(b|c=1) &= (0.216+0.096)/0.52 = \frac{31.2}{52}
\end{align}
$$
上記に基づいて$\displaystyle p(a,b|c=0) = \frac{9.6}{52} = \frac{16 \times 0.6}{52} = \frac{16}{52} \times \frac{31.2}{52} = p(a|c=1)p(b|c=1)$が成立する。
問題$8.12$
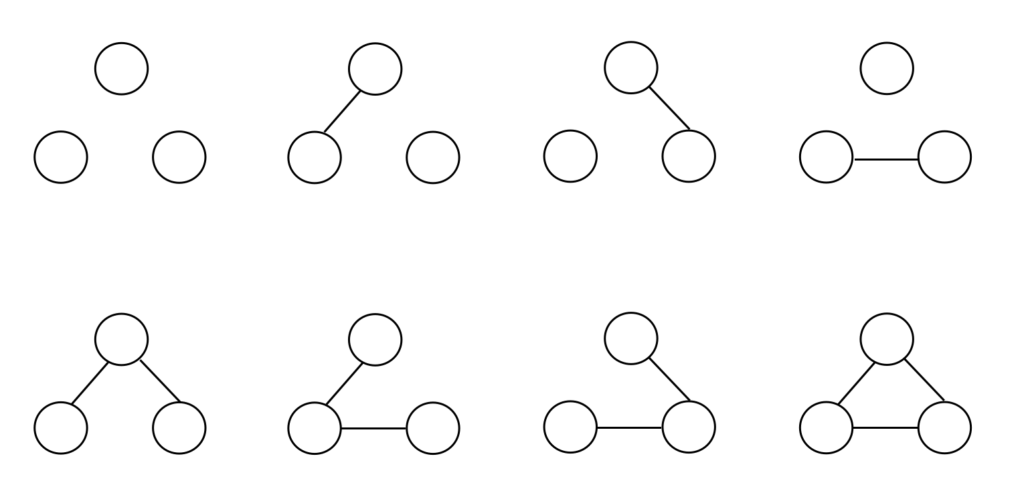
$M$個のノードの取り得るエッジの数は$\displaystyle {}_{M} C_{2} = \frac{M(M-1)}{2}$であるので、$M$個のノードに関する取り得るエッジの組み合わせは$\displaystyle 2^{\frac{M(M-1)}{2}}$通りある。下図に$M=3$で取り得るエッジの組み合わせを示した。