統計検定準1級対応の公式テキストである「統計学実践ワークブック」を1章から順に演習問題を中心に解説していきます。
今回は第3章「分布の特性値」です。
重要ポイント
第2章では確率関数を扱いました。確率変数は確率関数に従います。確率関数は確率分布とも呼ばれますが、この確率分布を代表する値について本章では扱っています。
期待値と分散
確率分布を代表する値として、期待値、分散が代表的です。期待値と分散については、こちらを参照ください。
期待値(平均)と分散は、単峰で対称な確率分布でよく使われますが、偏った分布の場合には別の指標を使ったほうが分布の位置や形状を把握するのに有効な場合があります。期待値のような分布の位置を表す値として、モード(mode、最頻値)や中央値(median)があります。単峰で対称な場合、期待値とこれらの指標は一致します。一方、分布の広がりを表現する値として四分位範囲があります。
共分散
確率変数が一つではない場合、分布の広がりを表す値として共分散があります。共分散についてもこちらを参照ください。
その他、テキストには細かい指標があります。ご確認ください。
演習問題解説
演習問題の全文は掲載しません。テキストは各自で用意するか、以下の抜粋から想像してください。
問3.1
ある動物群の平均体重が60kg、標準偏差が12kgだった。これらの動物の1ヶ月後の平均体重は65kgだったけど変動係数は変化なかった。
(1) 変動係数を求めよ
「変動係数」とは、標準偏差を平均値で割ったものです。標準偏差は「ばらつきの大きさ」の意味があり、値が大きいデータに対しては標準偏差は大きめになりがちです。そのため、平均値で割って正規化したという意味があります。
定義通りに以下のように導出できます。
$$
\begin{eqnarray}
\frac{\sqrt(V[X])}{E[X]} = \frac{12}{60} = 0.2
\end{eqnarray}
$$
(2) 1ヶ月後の体重の標準偏差を求めよ
問題には「変動係数は変化がなかった」と書かれています。そこで、以下の方程式が成り立ちます。
$$
\begin{eqnarray}
\frac{S}{65} &=& \frac{1}{5} \\
S &=& \frac{65}{5} = 13
\end{eqnarray}
$$
これも「変動係数」という量の定義を覚えていれば容易に解けます。
問3.2
以下の(1)~(3)の問いを「加重平均」、「幾何平均」、「調和平均」を使って算出せよ。
(1) 片道48kmの道のりを行きは8km/h、帰りは12km/hで往復した。往復の平均速度を求めよ。
速度は単位時間あたりに進む距離なので、割合と見ることができます。速度の平均なので、調和平均を適用すると平均速度を算出できます。
なお$x_1, \cdots, x_n$の調和平均$m_h$とは、以下の通り割合の平均の逆数で定義されています。
$$
m_h^{-1} = \frac{1}{n} \sum^{n}_{i=1} \left( \frac{1}{x_i} \right)
$$
なお、$m^{-1}$はmの逆数を表しています。
では、問題の回答に移ります。
$$
\begin{eqnarray}
m_h = \left\{ \frac{1}{2} \left( \frac{1}{8} + \frac{1}{12}\right) \right\}^{-1} = \frac{48}{5} = 9.6 [km/h]
\end{eqnarray}
$$
(2) 3種類の定食があり。それぞれの売り上げ数から、定食1食あたりの平均金額を求める。
テキストでは、A定食は600円、B定食は700円、C定食は500円であり、それぞれ、500食、700食、800食の売り上げがあったとされています。
愚直に計算しても良さそうですが、題意から「加重平均」を使って計算します。
重みをどう考えるかですが、それぞれの定食の売り上げ割合を重みとします。全体で2,000食売れていますので、A, B, Cの定食のそれぞれの売上数の割合は以下のようになります。
- A定食: $\frac{500}{2000} = \frac{1}{4}$
- B定食: $\frac{700}{2000} = \frac{7}{20}$
- C定食: $\frac{800}{2000} = \frac{2}{5}$
ということで以下のように平均金額を算出できます。
$$
m_w = 600\frac{1}{4} + 700\frac{7}{20} + 500 \frac{2}{5} = 150+245+200 = 595 [円]
$$
(3) 消費者物価指数の平均伸び率を求めよ。
消費者物価指数の4年間の伸び率が1.15, 0.98, 1.03, 0.99であったとされています。
「伸び率」は今年の値と翌年の値を割ったものです(前年の値$x_0$に伸び率$\alpha_0$をかければ翌年の値$x_1$になる, $x_1 = \alpha_0 x_0$、下図も参照)。そのため、4年後の値は初年度に各年の伸び率の総積をかけることで算出されます。

$$
\begin{eqnarray}
x_4 &=& \alpha_3 x_3 \\
x_3 &=& \alpha_2 x_2 \\
&\cdots&
\end{eqnarray}
$$
なので、初年度と4年後の関係は$x_4 = (\alpha_0 \cdot \alpha_1 \cdot \alpha_2 \cdot \alpha_3)x_0$となります。
「平均伸び率」を利用すると、上記の総積の部分が平均伸び率$\alpha$の4乗になります。ということで、幾何平均を用いれば良いということがわかります。
$$
\begin{eqnarray}
m_g = \sqrt[4]{\prod \alpha_i} = \sqrt[4]{1.15 \cdot 0.98 \cdot 1.03 \cdot 0.99} \simeq 1.04
\end{eqnarray}
$$
問3.3
以下の厚さのパンとハムを使ってサンドイッチを作る。
- パンの厚さX[mm]: E[X]=10, V[X] = $0.5^2$
- ハムの厚さY[mm]: E[Y]=3, V[Y] = $0.4^2$
サンドイッチを作る際に上記の材料を2通りの方法で作ることが考えられる。
- [方法1]
- 予めパンを二つに切断して貯めておく
- 溜め込んだパン片をランダムに抽出して、ランダムに選んだハムを挟んでサンドイッチを作る
- [方法2]
- パンを選びそれを二つに切断する
- 二つに切断したパンを使ってサンドイッチを作成する
二つの方法の違いですが、方法1は、サンドイッチを構成する2枚のパン片の厚さが異なります。一方、方法2では同じパンを使ってサンドイッチを作るので必ず2枚のパン片は同じ厚さになります。(下図参照)
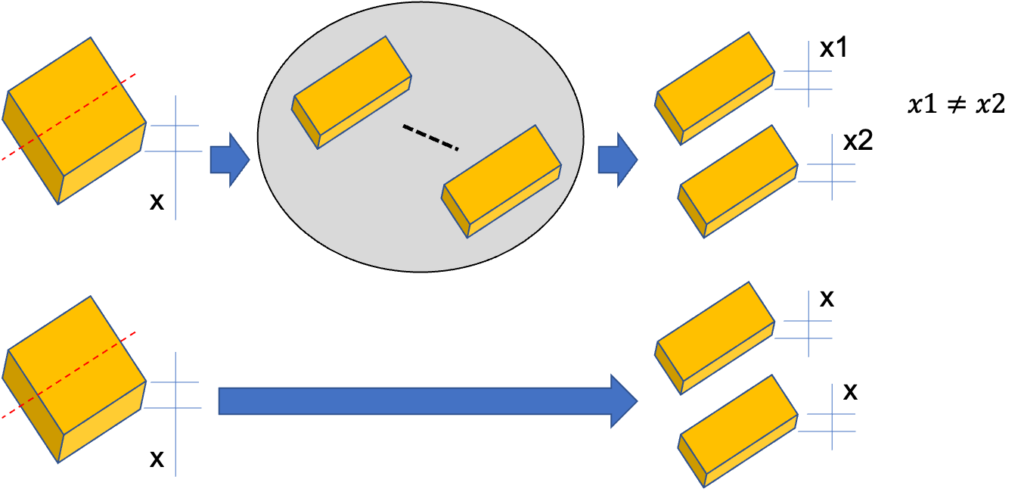
それぞれの方法で作成するサンドイッチの厚さの分散を求めよ
問題に書かれている二つのサンドイッチ作成方法から、方法1ではパン片が平均$E[X]$で分散$V[X]$にそれぞれ独立に従うことがわかります。厚さ$(E[X], V[X])$に従うパンを分けて溜め込んでおき、そこからランダムに選択しますので。一方、方法2ではパンを二つに分けてサンドイッチを作成するので、2つのパン片は同じ厚さになります。
方法1でのサンドイッチの厚さの分散は、次のように計算できます。
$$
\begin{eqnarray}
V[x_1 + x_2 + y] &=& V[x] + V[x] + V[y] \\
&=& 0.5^2 + 0.5^2 + 0.4^2 = 0.66
\end{eqnarray}
$$
一つ目の式変形は、$x_1, x_2$がそれぞれ独立であることを利用しています。
次に方法2での分散です。
$$
\begin{eqnarray}
V[2x + y] &=& 2^2 \cdot V[x] + V[y] \\
&=& 4 \cdot 0.5^2 + 0.4^2 = 1.16
\end{eqnarray}
$$
式変形は分散の性質を利用しています。
参考文献
ワークブック以外の参考資料として以下のものがおすすめです。
- 松原ら, 統計学入門, 1991, 東京大学出版会

