統計的時系列解析において、エルゴード性は観測データから理論的性質を推論するための基礎的な概念です。
エルゴード性は、「一つの時系列データを解析することでなぜ一般的な結論を導くことができるのか?」という根本的な疑問に回答するための重要な概念なのです。しかし、基礎的な概念であるがゆえに、暗黙的にエルゴード性が成り立つことを前提として議論が進められることが多いです。
本記事では、エルゴード性の定義、概念的な解釈、理論的意義、確認方法について解説します。
Contents
エルゴード性の概念
エルゴード性の基本的な考え方
エルゴード性とは、確率過程において「時間平均とアンサンブル平均が一致する」性質である。この性質により、単一の長い時系列データから、確率過程全体の統計的性質を推定することが可能となる。
参考までに、 データを読み解くリテラシー@NAIST EDGE では以下のように解釈が書かれている。
少し乱暴な言い方になるが,エルゴード性とは「個々の情報源に個性がないこと」と理解するのが早いように思われる.上記の参考ページを確認すると、具体例を交えて解説があるので、一読することをお勧めする。
エルゴード性の定義
任意の可測関数 $f$ に対して下記が成立する場合に、エルゴード性が成り立つという。
$$
\lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^T f(x_t) = E[f(x_t)]
$$
$f$ は恒等写像であったり、共分散が使われる。恒等写像の場合には特に「平均エルゴード性」、共分散の場合には「共分散エルゴード性」とも呼ばれる。
時間平均とアンサンブル平均の定義
アンサンブル平均
定義: 同一時刻における複数の実現値の平均
確率過程 $\{X_t\}$ について、時刻 $t$ でのアンサンブル平均は以下で定義される:
$$
E[X_t] = \int x \cdot f_t(x) dx
$$
ここで、$f_t(x)$ は時刻 $t$ における確率変数 $X_t$ の確率密度関数を表す。この関数は時刻 $t$ に依存し得るため、一般的に非定常過程では各時刻で異なる分布を持つ。
N個の実現系列(標本)がある場合は以下のように標本平均で近似する
$$
E[X_t] = \frac{1}{N} \sum_{i-1}^{N} x_t^{(i)}
$$
視覚的理解:
時刻1 時刻2 時刻3 ... 時刻k
系列1: X_1^(1) X_2^(1) X_3^(1) ... X_k^(1)
系列2: X_1^(2) X_2^(2) X_3^(2) ... X_k^(2)
系列3: X_1^(3) X_2^(3) X_3^(3) ... X_k^(3)
⋮ ⋮ ⋮ ⋮ ⋮
系列N: X_1^(N) X_2^(N) X_3^(N) ... X_k^(N)
↓ ↓ ↓ ↓
E[X_1] E[X_2] E[X_3] ... E[X_k]
(縦方向の平均 = アンサンブル平均)時間平均
定義: 一つの実現における時間方向の平均
一つの実現系列 ${X_t^(i)}$ について
$$
時間平均 = \lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^{T} x_t^{(i)}
$$
視覚的理解:
系列i: X_1^(i) → X_2^(i) → X_3^(i) → ... → X_T^(i)
└─────────────────────────────────┘
時間平均
(横方向の平均 = 時間平均)平均エルゴード性の定義と意義
平均エルゴード性の数学的定義
平均エルゴード性は以下の条件で定義される
$$
\lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^{T} x_t = E[x_t]
$$
これは、1章でも述べた「時間平均=アンサンブル平均」が成立することを意味する。
定常過程における平均エルゴード性
定常過程の基では、$E[x_t] = \mu$ (アンサンブル平均が時間依存せず一定) であるため、平均エルゴード性は以下のように表現される
$$
\lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^{T} x_t = E[x_t] = \mu
$$
平均エルゴード性と標本平均
定常性に関して解説した記事では、定常性の下で標本平均や標本分散で過程の平均と分散を近似すると解説したが、暗黙的にエルゴード性が成り立つことを前提としている。正確には以下の順序で標本平均が理論平均を近似する。
- 弱定常の定義:$E[y_t] = \mu$ 理論平均が時間に依存せず一定
- 理論平均の近似:E[y_t] = \frac{1}{N} \sum_{i-1}^{N} y_t^{(i)} 複数の標本がある場合に、理論平均を標本平均で近似(アンサンブル平均)
- 平均エルゴード性:$E[y_t] = \lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^{T} y_t$ アンサンブル平均は時間平均と一致する
- 時間平均を標本平均で近似:$\bar{y} = \frac{1}{T} \sum_{t=1}^{T} y_t \approx E[y_t]$
このように、時系列解析においては定常性の仮定とともに、エルゴード性が成り立つことを前提として議論が進められていることが多い。エルゴード性が成り立た無いような系列(後述)では、そもそも統計的時系列解析の基礎が成り立たないため、注意が必要である。
時系列データとエルゴード性
エルゴード性が成り立つ具体例
基本的には、分析で扱う時系列データはエルゴード性が成り立つ。
ホワイトノイズ
ホワイトノイズは、時系列モデルのノイズ成分としてよく利用される。定義は下記の通り
全ての時点 $t$ においていかが成立するとき、系列 $\epsilon_t$ はホワイトノイズ(white noise) と呼ばれる。
$$
\begin{align}
E( \epsilon_t ) &= 0 \\
E( \epsilon_t^2 ) &= \sigma^2 \\
E( \epsilon_t \epsilon_{t-k} ) &= 0 \\
\end{align}
$$
つまり、平均と共分散が0である系列である。なお、ホワイトノイズは特定の確率分布に限定されないが、正規分布に従うホワイトノイズを正規ホワイトノイズと呼ぶ。
$\sigma^2=1.0$の正規ホワイトノイズを1系列サンプルすると例えば以下のような系列となる。
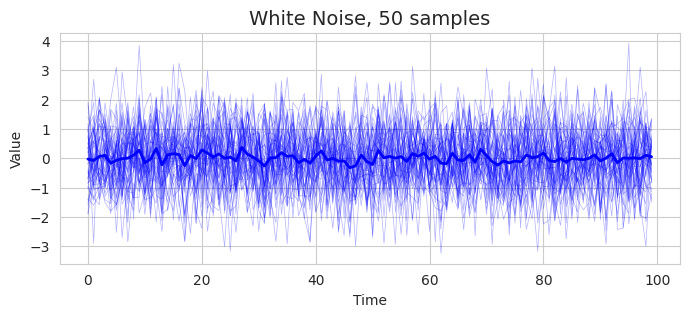
正規ホワイトノイズを50サンプル生成し、平均を太線で表示したものが下記の図である。特別傾向はみられず、平均すると0付近に落ち着いていることがわかる。
AR(1)過程
AR過程(Autoregressive process, 自己回帰過程)とは、自身$y_t$の過去の値($y_{t-1}, y_{t-2},,,$)に回帰された形で表現される過程である。特に、一つ前の過去の値$y_{t-1}$にのみ依存する場合を AR(1) 過程と呼ぶ。
$$
y_t = c + \phi_1 y_{t-1} + \epsilon_t, \quad \epsilon_t \sim \mathrm{W.N.}(\sigma^2)
$$
特に、エルゴード性が成り立つ(弱定常が成り立つ)ためには、$|\phi| < 1$であることが必要である(出なければ発散してしまう)。
$\phi=0.8, c=1.0$のAR(1)過程は例えば以下のような系列となる。
これを50系列サンプルすると以下のようにプロットされる。
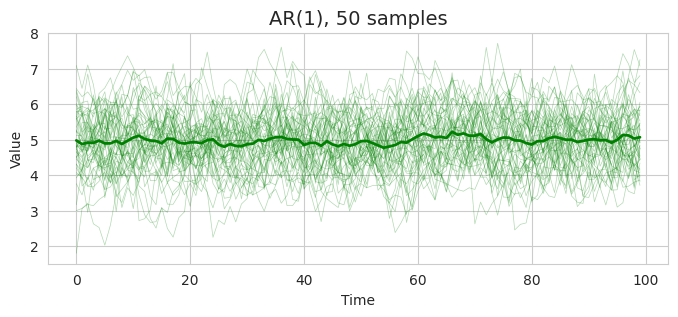
50サンプルの結果ではわかりにくいが、正規ホワイトノイズと比べて、バラつきが抑えられ、各点間に依存性が見えそうな系列であることがわかる。
エルゴード性が成り立たない具体例
エルゴード性が成り立たない系列としては、定常性が成り立たない系列が挙げられる(先の2系列)。特殊な系列だが、定常性は成り立つのに、エルゴード性が成り立たない系列というのもある。
ランダムウォーク
ランダムウォークは、以下の式で定義される。
$$
y_t = c + y_{t-1} + \epsilon_t, \quad \epsilon_t \sim \mathrm{W.N.}(\sigma^2)
$$
これは、 AR係数(回帰係数)$\phi$が1のAR(1)過程である。AR係数が1ということは、過去の値をそのまま減衰させずにノイズを加算していくため、収束しない。1系列と50系列のサンプル結果を以下に示す。
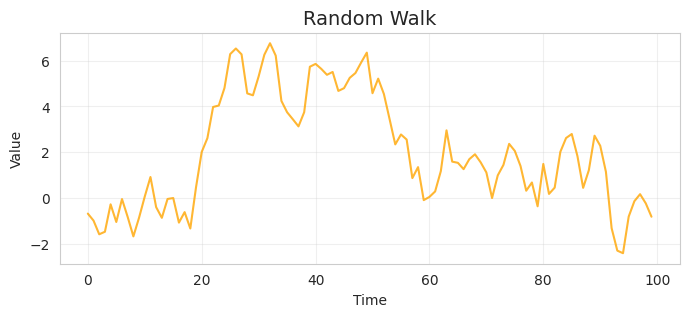
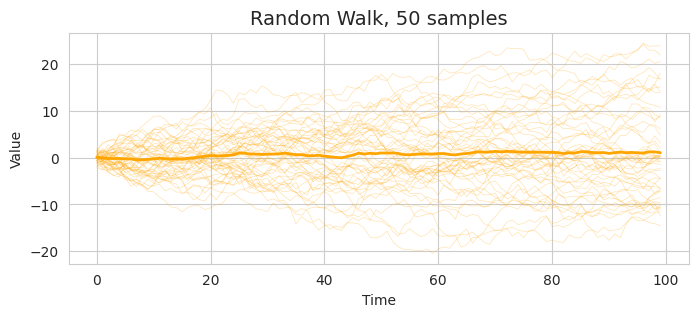
ランダムウォークはそもそも定常ではないため、エルゴード性も成り立たない。なお、AR過程が定常である条件は $\phi < 1$。
確率的正弦波+ノイズ
確率的正弦波を以下のように定義する。
$$
x_t = A \cdot \sin(2 \pi \cdot f \cdot t + \phi) + \epsilon_t
$$
ここで、$A \sim N(\mu_A, \sigma_A^2)$, $\phi \sim \mathrm{Uniform}(0, 2\pi)$ 。つまり、振幅と位相が標本ごとに確率的に変動するという過程である。
この過程を5標本プロットすると以下のようになる。
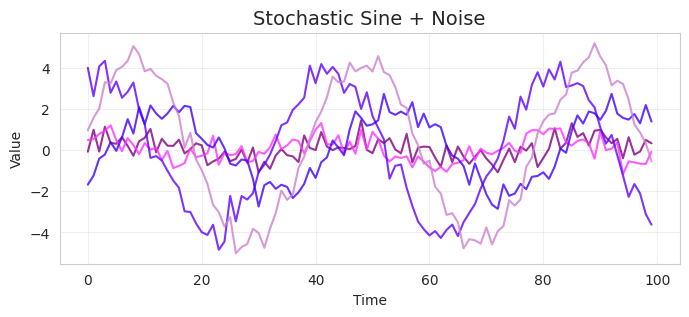
この過程について、詳しく見てみる。
まずは定常性を確認する。
時間平均については、それぞれの標本を考えると正弦波であるため、0となることがわかり、時間依存しない。
自己共分散は以下のように、時間依存しないことがわかる。
$$
\begin{aligned}
\operatorname{Cov}\left(y_t, y_{t-1}\right) & =E\left[\left(y_t-\mu\right)\left(y_{t+k}-\mu\right)\right] \\
& =E[X \sin (2 \pi f t+\theta) \cdot X \sin (2 \pi f(t+k)+\theta)] \\
& =E\left[x^2\right] \frac{1}{2} E[\cos (2 \pi f k)-\cos (4 \pi f t+2 \theta+2 \pi f k)] \\
& =\frac{\sigma^2}{2} \cos (2 \pi f k)-\sigma^2 E[\cos (2 \pi f t+\pi f k+\theta)] \\
& =\frac{\sigma^2}{2} \cos (2 \pi f k)-\sigma^2 E[\cos (\alpha+\theta)] \\
& =\frac{\sigma^2}{2} \cos (2 \pi f k)-\sigma^2 E[\cos (\alpha) \cos (\theta)-\sin (\alpha) \sin (\theta)] \\
& =\frac{\sigma^2}{2} \cos (2 \pi f k)-\sigma^2{\cos (\alpha) E(\cos (\theta)]-\sin (\alpha) E[\sin (\theta)]} \\
& =\frac{\sigma^2}{2} \cos (2 \pi f k)
\end{aligned}
$$
これで、本系列は弱定常であることがわかる。
一方、標本ごとの共分散を調べると以下のようになる。
$$
\begin{aligned}
\lim _{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^T y_t y_{t+k} & =\lim _{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^T X \sin (2 \pi f t+\theta) X \sin (2 \pi f(t+k)+\theta) \\& =\lim _{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^T\left\{\frac{x^2}{2} \cos (2 \pi f k)-\frac{x^2}{2} \cos (4 \pi f t+2 \theta+2 \pi f k)\right\} \\
& =\frac{x^2}{2} \cos (2 \pi f k)
\end{aligned}
$$
系列毎の共分散はXに依存することがわかる。Xは確率変数であり、系列に依存して変わる。そのため、自己共分散と同一にならず、エルゴード性が成り立たないことがわかる。
まとめ
エルゴード性の概念は、統計的時系列解析において「なぜ一つのデータから一般的な結論を導けるのか」という根本的な問いに対する数学的な答えを提供する。この理解は、より高度な時系列モデリング、非線形時系列解析、機械学習における時系列データの扱いなど、様々な発展的トピックへの基礎となる極めて重要な概念である。
しかしながら、エルゴード性については暗黙的に成り立つとして議論が進められることが多いため、本記事で改めてまとめた。
