Contents
過去問題
過去問題は統計検定公式が問題と解答例を公開しています。こちらを参照してください。
解答
[1] 解答
(1) $\boxed{ \ \mathsf{23}\ }$ : ③
(ア)の予測値に対する残差のプロットから、$29$(USA)の予測値はおよそ$84$、残差はおよそ$-5.5$であるとわかる。これに一番近い選択肢は$3$である。
(2) $\boxed{ \ \mathsf{24}\ }$ : ⑤
てこ値が大きい観測値の方がモデルへの影響力は大きいため、誤りである。
(統計学実践ワークブック第$17$章等を参照)
[2] 解答
(1) $\boxed{ 記述\ 8 }$
(ア)を見ると,残差が$-4$より小さい(絶対値が大きい)点の個数がモデル$1$よりもモデル$2$の方が少なく、モデル$2$の方が推定が良くなっていることが読み取れる。
従って、決定係数が大きいのはモデル$2$である。
(2) $\boxed{ 記述\ 9 }$
問の表から、日本の平均寿命は$83.4$である。つまり、残差を$y$、予測値を$x$とすると、$y+x=83.4$の関係式を満たす。
したがって$y=-x+83.4$と変形できることから、点$(83.4,0)$を通り、傾き$-1$の直線上の点がJPNである。(図は省略)
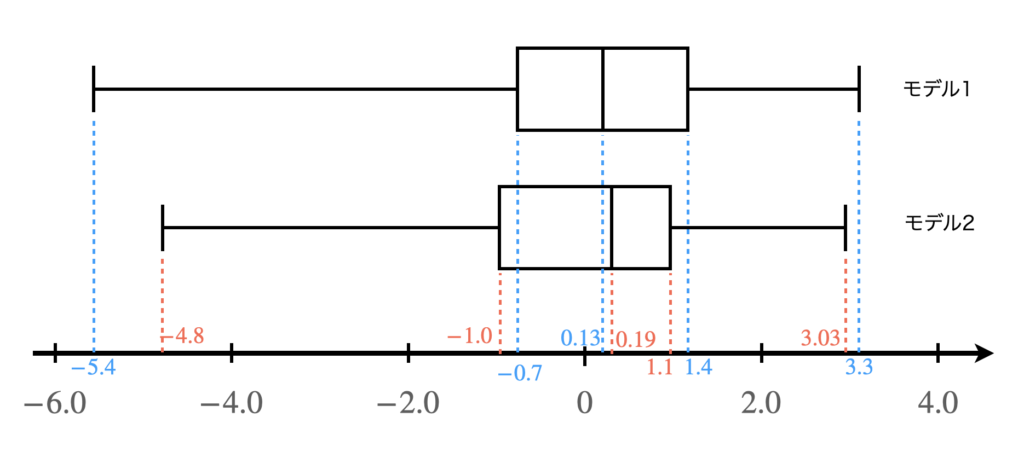
(3) $\boxed{ 記述\ 10 }$
箱髭図は下記の通りとなる。