過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定2級(2016.11)【正解】(統計検定公式)
問9 解答
(ポアソン分布,正規近似)
[1]
$\boxed{ \ \mathsf{16}\ }$ ①
ポアソン分布の分散は平均(期待値)に等しい。
[2]
$\boxed{ \ \mathsf{17}\ }$ ⑤
平均$\lambda$が20以上のポアソン分布は正規分布で近似できるので
$X\sim Po(\lambda)\approx N(\lambda,\lambda)$
よって,確率変数$Z=\displaystyle\frac{X-\lambda}{\sqrt{\lambda}}$は標準正規分布に従う。
$\lambda=50$なので
$$P(X>60)=P\left(Z>\frac{60-50}{\sqrt{50}}\right)\fallingdotseq P(Z>1.41)=0.0793$$
※)正規近似でより正確な値を求めるためには,確率変数が$X=x$となる場合$x\pm0.5$の範囲の確率で近似することが適当である。上の場合$P(X>60)$のかわりに$P(X>60+0.5)$で求める方がより正確となる。(連続修正)
$$P(X>60.5)=P\left(Z>\frac{60.5-50}{\sqrt{50}}\right)\fallingdotseq P(Z>1.48)=0.0694$$
[3]
$\boxed{ \ \mathsf{18}\ }$ ③
$30$人の事前登録者に追加参加を足したら記念品個数$x$を超す確率が$0.05$なので,
$$P(X+30>x)=0.05\ \Rightarrow\ P(X>x-30)=0.05$$
[2]同様,確率変数$Z=\displaystyle\frac{X-\lambda}{\sqrt{\lambda}}$は標準正規分布に従う。$\lambda=20$なので
$$P\left(Z>\frac{x-30-20}{\sqrt{20}}\right)=0.05$$
標準正規分布表から
$$\frac{x-30-20}{\sqrt{20}}=1.645\ \Rightarrow\ x\fallingdotseq57$$
※)前問同様,連続修正を用いた場合
$$\begin{eqnarray}
&P(X+30>x+0.5)=0.05\ \Rightarrow\ P(X>x-29.5)=0.05\\
&P\left(Z>\frac{x-29.5-20}{\sqrt{20}}\right)=0.05\\
&\frac{x-29.5-20}{\sqrt{20}}=1.645\ \Rightarrow\ x\fallingdotseq57
\end{eqnarray}$$
ポアソン分布について
ポアソン分布は,二項分布$B(n,p)$において期待値$np=\lambda$を固定し,試行回数と成功確率について$n\rightarrow\infty,\ p\rightarrow0$のような極限を取った時に得られる確率分布として定義される。(『まれに起きる現象』に対する確率モデルともいわれる。)
・確率変数$X$はパラメータ$\lambda$のポアソン分布に従うとする。$X$の確率関数は,
$$p(x)=P(X=x)=\frac{\lambda^x}{x!}e^{-\lambda}\ \ \ (x=0,1,2,\dots)$$
(証明)
ポアソン分布の定義から,試行回数$n$,成功確率$p$の二項分布$B(n,p)$(確率関数:$f(x)={}_nC_xp^x(1-p)^{n-x}$)で$\lambda=np$とおき,$n\rightarrow\infty(p\rightarrow0)$とした極限の分布であるから,$\lambda=np\Rightarrow p=\lambda/n$を用いて二項分布の確率関数を変形すると,
$$\begin{align}
f(x)&={}_nC_xp^x(1-p)^{n-x}=\frac{n(n-1)\cdots(n-x+1)}{x!}\left(\frac\lambda n\right)^x\left(1-\frac\lambda n\right)^{n-x}\\ &=\frac{\lambda^x}{x!}\frac{n(n-1)\cdots(n-x+1)}{n^x}\left(1-\frac\lambda n\right)^{n-x}
\end{align}$$
ここで,
$$\begin{align}
\frac{n(n-1)\cdots(n-x+1)}{n^x}&=\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-x+1}{n}\\
&=1\times\left(1-\frac1n\right)\times\cdots\times\left(1-\frac{x-1}n\right)
\end{align}$$
$n\rightarrow\infty$のとき,$\begin{align}1-\frac1n\rightarrow0,\cdots,1-\frac{x-1}n\rightarrow0\end{align}$となるので,上式は$1$となる。また,ネイピア数の性質から,
$$\lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n=e^x$$
なので,$n\rightarrow\infty$のとき,
$$\left(1-\frac\lambda n\right)^{n-x}=\left(1+\frac{-\lambda}n\right)^{n}\left(1-\frac\lambda n\right)^{-x}=e^{-\lambda}\times(1-0)^{-x}=e^{-\lambda}$$
以上から,$n\rightarrow\infty$のとき,
$$f(x)=\frac{\lambda^x}{x!}e^{-\lambda}$$
である。
・ポアソン分布の期待値は$\lambda$,分散も$\lambda$である。
(証明)
$$\begin{align}
E[X]=&\sum_{x=0}^\infty x\frac{\lambda^x}{x!}e^{-\lambda}=e^{-\lambda}\sum_{x=1}^\infty\frac{\lambda\times\lambda^{x-1}}{(x-1)!}=e^{-\lambda}\lambda\sum_{k=0}^\infty\frac{\lambda^k}{k!}\\
=&e^{-\lambda}\lambda e^{\lambda}=\lambda\\
E[X(X-1)]=&\sum_{x=0}^\infty x(x-1)\frac{\lambda^x}{x!}e^{-\lambda}=e^{-\lambda}\sum_{x=2}^\infty\frac{\lambda^2\times\lambda^{x-2}}{(x-2)!}=e^{-\lambda}\lambda^2\sum_{k=0}^\infty\frac{\lambda^k}{k!}\\
=&e^{-\lambda}\lambda^2 e^{\lambda}=\lambda^2\\
\therefore\ V[X]=&E[X(X-1)]+E[X]-E[X]^2=\lambda^2+\lambda-\lambda^2=\lambda
\end{align}$$
(少し難しい証明)
ポアソン分布のモーメント母関数(積率母関数)は
$$\begin{align}
M_X(t)=&E[e^{tx}]=\sum_{x=0}^\infty e^{tx}\frac{\lambda^x}{x!}e^{-\lambda}=e^{-\lambda}\sum_{x=0}^\infty \frac{(e^t\lambda)^x}{x!}\\
=&e^{-\lambda}\times\mathrm{exp}(e^t\lambda)=\mathrm{exp}[\lambda(e^t-1)]
\end{align}$$
これを用いて,$E[X],V[X]$を求める。
$$\begin{align}
M_X'(t)&=\frac{d}{dt}M_X(t)=\frac{d}{dt}\mathrm{exp}[\lambda(e^t-1)]=\lambda e^t\mathrm{exp}[\lambda(e^t-1)]\\
M_X”(t)&=\frac{d}{dt}M_X'(t)=\frac{d}{dt}\lambda e^t\mathrm{exp}[\lambda(e^t-1)]=\lambda e^t(1+\lambda e^t)\mathrm{exp}[\lambda(e^t-1)]\\
\therefore\ E[X]&=M_X'(0)=\lambda e^0\mathrm{exp}[\lambda(e^0-1)]=\lambda\\
E[X^2]&=M_X”(0)=\lambda e^0(1+\lambda e^0)\mathrm{exp}[\lambda(e^0-1)]=\lambda(1+\lambda)\\
\therefore\ V[X]&=E[X^2]-E[X]^2=\lambda(1+\lambda)-\lambda^2=\lambda
\end{align}$$
問10 解答
(連続型確率変数,確率密度関数)
[1]
$\boxed{ \ \mathsf{19}\ }$ ①
$$\begin{align}
E[X]=&\int_{-1}^0x(x+1)dx+\int_0^1x(-x+1)dx\\
=&\left[\frac13x^3+\frac12x^2\right]_{-1}^0+\left[-\frac13x^3+\frac12x^2\right]_0^1\\
=&\frac13-\frac12-\frac13+\frac12=0\\
V[X]=&E[X^2]-E[X]^2\\
=&\int{-1}^0x^2(x+1)dx+\int_0^1x^2(-x+1)dx\\
=&\left[\frac14x^4+\frac13x^3\right]_{-1}^0+\left[-\frac14x^4+\frac13x^3\right]_0^1\\
=&-\frac14+\frac13-\frac14+\frac13=\frac16\\
\end{align}$$
[2]
$\boxed{ \ \mathsf{20}\ }$ ③
確率密度関数のグラフは以下のとおり
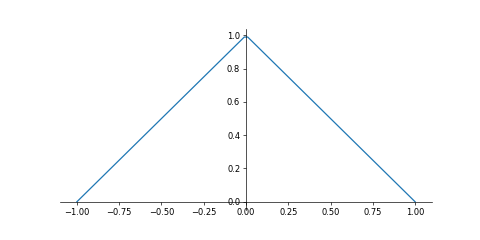
グラフから確率変数$X$の中央値は$0\ \ \left(\displaystyle P(X\le0)=\int_{-1}^0f(x)dx=\frac12\right)$
なので,第1四分位数は$-1\ge X<0$の間にある。
$$\begin{align}
P(X\le a)=\int_{-1}^a(x+1)dx=&\frac14\\
\left[\frac12x^2+x\right]_{-1}^a=&\frac14\\
\frac12a^2+a+\frac12=&\frac14\\
2(a^2+2a+1)-1=&0\\
(a+1)^2=&\frac12\\
a+1=&\pm\sqrt{\frac12}\\
a=&-1\pm\frac{\sqrt{2}}2\\
\end{align}$$
このうち,$-1\ge a<0$を満たすのは $\displaystyle a=-1+\frac{\sqrt{2}}2$
問11 解答
(標本平均の期待値・分散,不偏性)
[1]
$\boxed{ \ \mathsf{21}\ }$ ③
$$E[X_1^2]=V[X_1]+E[X_1]^2=\sigma^2+\mu^2$$
[2]
$\boxed{ \ \mathsf{22}\ }$ ②
$$\begin{align}
\sum_{i=1}^n(X_i-\bar X)^2=&\sum_{i=1}^n{(X_i-\mu)-(\bar X-\mu)}^2\\
=&\sum_{i=1}^n{(X_i-\mu)^2-2(X_i-\mu)(\bar X-\mu)+(\bar X-\mu)^2}\\
=&\sum_{i=1}^n(X_i-\mu)^2-2\sum_{i=1}^n(X_i-\mu)(\bar X-\mu)+\sum_{i=1}^n(\bar X-\mu)^2\\
=&\sum_{i=1}^n(X_i-\mu)^2-2n(\bar X-\mu)^2+n(\bar X-\mu)^2\\
=&\sum_{i=1}^n(X_i-\mu)^2-n(\bar X-\mu)^2\\
E\left[\sum_{i=1}^n(X_i-\bar X)^2\right]=&E\left[\sum_{i=1}^n(X_i-\mu)^2-n(\bar X-\mu)^2\right]\\
=&\sum_{i=1}^nE\left[(X_i-\mu)^2\right]-nE\left[(\bar X-\mu)^2\right]\\
=&\sum_{i=1}^nV\left[X_i\right]-nV\left[\bar X\right]\\
=&n\sigma^2-nV\left[\frac1n\sum_{i=1}^nX_i\right]\\
=&n\sigma^2-n\left(\frac1n\right)^2\sum_{i=1}^nV\left[X_i\right]\\
=&n\sigma^2-n\left(\frac1n\right)^2n\sigma^2=(n-1)\sigma^2\\
\therefore \ E\left[\frac1{n-1}\sum_{i=1}^n(X_i-\bar X)^2\right]=&\frac1{n-1}E\left[\sum_{i=1}^n(X_i-\bar X)^2\right]=\sigma^2
\end{align}$$
よって,$\displaystyle\frac1{n-1}\sum_{i=1}^n(X_i-\bar X)^2$は$\sigma^2$の不偏推定量である。また,
$$\begin{align}
\sum_{i=1}^n(X_i-\bar X)^2=&\sum_{i=1}^n(X_i^2-2X_i\bar X+\bar X^2)\\
=&\sum_{i=1}^nX_i^2-2\sum_{i=1}^nX_i\bar X+\sum_{i=1}^n\bar X^2\\
=&\sum_{i=1}^nX_i^2-n\bar X^2\\
E\left[\sum_{i=1}^n(X_i-\bar X)^2\right]=&E\left[\sum_{i=1}^nX_i^2-n\bar X^2\right]\\
=&\sum_{i=1}^nE\left[X_i^2\right]-nE\left[\bar X^2\right]\\
\therefore \ E\left[\bar X^2-\frac{\hat\sigma^2}n\right]=&E\left[\bar X^2\right]-\frac1nE\left[\hat\sigma^2\right]\\
=&\frac1n\left(\sum_{i=1}^nE\left[X_i^2\right]-E\left[\sum_{i=1}^n(X_i-\bar X)^2\right]\right)-\frac1nE\left[\hat\sigma^2\right]\\
=&\frac1n\left\{n\left(\sigma^2+\mu^2\right)-(n-1)\sigma^2\right\}-\frac1n\sigma^2\\
=&\sigma^2+\mu^2-\frac{n-1}n\sigma^2-\frac1n\sigma^2\\
=&\mu^2
\end{align}$$
よって,$\displaystyle\bar X^2-\frac{\hat\sigma^2}n$は$\mu^2$の不偏推定量である。
問12 解答
(母比率の検定)
[1]
$\boxed{ \ \mathsf{23}\ }$ ④
確率変数$X_i$は独立に成功確率$p$のベルヌーイ分布に従う。
この試行を$n$回繰り返した時の成功回数$\sum X_i$は二項分布$B(n,p)$に従う。したがって,$\sum X_i$の分散は$np(1-p)$である。
$$\begin{align}
V\left[\hat p\right]=&V\left[\frac1n\sum_{i=1}^nX_i\right]\\
=&\left(\frac1n\right)^2V\left[\sum_{i=1}^nX_i\right]\\
=&\frac1{n^2}np(1-p)\\
=&\frac1np(1-p)\\
=&\frac1n\left(-p^2+2\times\frac12p-\frac14+\frac14\right)\\
=&\frac1n\left\{-\left(p-\frac12\right)^2+\frac14\right\}
\end{align}$$
よって,$V\left[\hat p\right]$の最大値は$\displaystyle p=\frac12$のとき$\displaystyle\frac1{4n}$となる。
[2]
$\boxed{ \ \mathsf{24}\ }$ ⑤
帰無仮説 $H_0:p=p_0$,対立仮説 $H_1:p\ne p_0$なので,両側検定となる。
$Z$は標準正規分布で近似できるので,$$|Z|>z_{0.05/2}=1.96$$が棄却域となる。
検定統計量が棄却域にあるとき帰無仮説を棄却する。
問13 解答
(独立性の検定)
独立性の検定は,2つの属性$A,B$が独立かどうかの検定である。
属性$A$のカテゴリが$A_i$,属性$B$のカテゴリが$B_j$の観測度数を$f_{ij}=O_{ij}$とし,
$f_{i\cdot}=\sum_jf{ij}$を$i$行の度数合計(行和),
$f_{\cdot j}=\sum_if{ij}$を$j$列の度数合計(列和),
$f_{\cdot\cdot}=\sum_i\sum_jf_{ij}=\sum_if_{i\cdot}=\sum_jf_{\cdot j}=n$を全度数合計という。
属性$A,B$が独立という帰無仮説は,$H_0:P(A\cap B)=P(A)P(B)$が成り立つことである。
ここで,カテゴリ$A_i,B_j$の出現確率はそれぞれ$f_{i\cdot}/n,f_{\cdot j}/n$であるので,$H_0$のもとで,属性$A$のカテゴリが$A_i$,属性$B$のカテゴリが$B_j$の期待度数は
$$E_{ij}=n(f_{i\cdot}/n)(f_{\cdot j}/n)=f_{i\cdot}f_{\cdot j}/n$$
となる。
帰無仮説$H_0$の下で,次検定の統計量$\chi^2$は度数が大きいときに近似的に$\chi^2$分布に従う。行和と列和が固定されていることから自由度は$(r$(行の数)$-1)\times(c$(列の数)$-1)$となる。
$$\chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\sim\chi^2((r-1)(c-1))$$
有意水準$100\alpha\%$で帰無仮説が棄却されるには,$\chi^2$分布の上側$\alpha$点より上で求めた$\chi^2$統計量が大きくなればよい。
[1]
$\boxed{ \ \mathsf{25}\ }$ ④
夏季と冬季の分布の同等性は,両者が独立であるかを検定すればよい。
夏季と冬季の各階級の死者数についてクロス集計表を作成すると以下のとおりである。
| $60\sim100$ | $100\sim120$ | $120\sim140$ | $140\sim160$ | $160\sim200$ | 計 | |
| 夏季 | $18$ | $42$ | $24$ | $11$ | $1$ | $96$ |
| 冬季 | $13$ | $25$ | $23$ | $19$ | $16$ | $96$ |
| 合計 | $31$ | $67$ | $47$ | $30$ | $17$ | $192$ |
夏季の「100人以上120人未満」の階級の期待度数は
$$\frac{67\times96}{192}=33.5$$
[2]
$\boxed{ \ \mathsf{26}\ }$ ②
自由度は$(5-1)\times(2-1)=4$
[3]
$\boxed{ \ \mathsf{27}\ }$ ①
自由度が$4$のカイ二乗分布の上側$5\%$点の値は$9.49$で,統計検定量はこれより大きいので,帰無仮説は棄却され,両者は独立でない,すなわち,2つの分布は同等でない。(分布は季節に関係している。)
問14 解答
(2つの母平均の差の検定(対応のある場合))
$\boxed{ \ \mathsf{28}\ }$ ②
対応のある2つの標本に関して,対をなす値から求められる1つの値(例えば差)を用いることで,1標本の検定の問題に帰着される。この問題では対応する2つの値の差を用いて,2標本の母平均の差について検定を行う。
各月の増分は独立に同一の正規分布に従うので,増分が$0$等しいという仮定の下で,サンプル数を$n$,標本平均を$\bar X$,不偏標準偏差を$s$とすると,統計量
$$t=\frac{\bar X-0}{s/\sqrt{n}}$$は自由度$n-1$の$t$分布にしたがう。(母分散の値が未知の時の母平均の検定と同じ考え)
問題は$n=12$(データは12対),$\bar X=-13.1$,$s=19.9$なので,
$$t=\frac{-13.1}{19.9/\sqrt{12}}\fallingdotseq-2.28$$となり,自由度は$n-1=11$である。
【補足】有意水準$5\%$で両側検定を行うと
$$t_{0.025}(11)=2.201\ \rightarrow\ t=-2.28<-t_{0.025}(11) $$となり,帰無仮説は棄却され,2標本の母平均に差がみられる。
また,有意水準$1\%$で両側検定を行うと
$$t_{0.005}(11)=3.106\ \rightarrow\ t=-2.28>-t_{0.005}(11)$$となり,帰無仮説は棄却されない。
問15 解答
(標本平均,分散。中心極限定理,仮説検定の理論)
[1]
$\boxed{ \ \mathsf{29}\ }$ ④
(ア) 確率変数$X_1,\dots,X_n$が独立で同一の正規分布$N(0,\sigma^2)$に従うとき,標本平均は
$$\bar X=\frac1n\sum_{t=1}^nX_t\sim N\left(0,\frac{\sigma^2}n\right)$$となる。したがって,求める分散は$\displaystyle\frac{\sigma^2}{21}$となる。
[2]
$\boxed{ \ \mathsf{30}\ }$ ①
(イ) 検定統計量$\displaystyle Z=\frac{\bar X}{\sigma/\sqrt{21}}$は帰無仮説の下で標準正規分布に従うので,有意水準$5\%$の両側検定では標準正規分布の上側$2.5\%$点を用いて,$$|Z|>z_{0.025}=1.96$$が棄却域となる。
(ウ) 母分散$\sigma^2$が未知のとき,検定統計量$\displaystyle T=\frac{\bar X}{\hat\sigma/\sqrt{21}}$は帰無仮説の下で自由度$21-1=20$の$t$分布に従うので,有意水準$5\%$の両側検定では自由度$20$の$t$分布の上側$2.5\%$点を用いて,$$|T|>t_{0.025}(20)=2.086$$が棄却域となる。
(エ) $X_t$が正規分布に従わない場合,中心極限定理に基づいた正規近似を用いるため,検定統計量$T$の分布は標準正規分布で近似される。したがって,有意水準$5\%$の両側検定では標準正規分布の上側$2.5\%$点を用いて,$$|T|>z_{0.025}=1.96$$が棄却域となる。
[3]
$\boxed{ \ \mathsf{31}\ }$ ①
(オ) $P(Z>0.63)=0.2643$なので,両側検定の場合$P_-$値は$2\times0.2643=0.5286$。
(カ) ここで,$P_-$値は$5\%$より大きいので,帰無仮説は棄却されない。
問16 解答
(単回帰モデル,統計ソフトウェアの活用)
※重回帰モデルの統計ソフトウェアによる出力結果の主な項目
$\mathtt{Estimate}$:回帰係数($\alpha,\beta_1,\beta_2,\beta_3$)の推定値
$\mathtt{Std.Error}$:回帰係数の推定値の標準誤差
$\mathtt{t\ value}$:$t$値,$\mathtt{Pr(\gt|t|)}$:$P_-$値・・・回帰係数の検定で使う
$\mathtt{Rasidual\ standard\ error}$:誤差項の標準偏差の推定値
$\mathtt{degrees\ of\ freedom}$:自由度
$\mathtt{Multiple\ R-squared}$:決定係数($R^2$)
$\mathtt{Adjusted\ R-squared}$:自由度調整済み決定係数($R^{*2}$)
$\mathtt{F-statistic}$:$F$検定統計量,$\mathtt{p-value}$:$P_-$値・・・回帰の有意性の検定で使う
[1]
$\boxed{ \ \mathsf{33}\ }$ ④
① この回帰モデルの自由度は,標本の大きさ$197$から推定する回帰係数の数$2$を引いた値の$195$である。誤り。
② 決定係数はこのモデルの当てはまりの尺度であり,予測の的中率を表すものではない。誤り。
③ 単回帰モデルでは,被説明変数を説明変数に回帰した場合の説明変数の回帰係数の推定値は,
説明変数と被説明変数の標本共分散/説明変数の標本分散
である。したがって,説明変数と被説明変数を入れ替えたときに,一方の推定値がもう一方の推定値の逆数となるためには,それぞれの変数の標本分散が等しいときである。今回のケースでは,散布図から2つの変数の標本分散が異なることは明らかである。誤り。
④ 回帰モデルで推定された残差の総和は$0$であるので,残差の平均も$0$であり,中央値よりも大きくなる。正しい。
⑤ 「$\mathtt{F-statistic}$」はモデルの中に説明力のある(回帰係数$\ne0$)変数(定数項を除く)が含まれているかを判断する$F$検定の統計量である。誤り。
[2]
$\boxed{ \ \mathsf{34}\ }$ ①
Creの観測値の最小値に対応する残差は,散布図の観測値の点と回帰直線の間隔から20よりやや小さい値となっている。これを選択肢の図についてみると,あてはまるのは①の図である。Creの観測値の上位10位の点についてみても,すべて残差は$\pm10$以内であるが,これについてもあてはまるのは①の図である
(なお,③の図は残差の正負が逆になっている図で,④の図では残差の平均が明らかに$0$,②は残差のばらつきが大きくなっている。)
[3]
$\boxed{ \ \mathsf{35}\ }$ ②
回帰係数の区間推定は$n=197$と大きいので,正規近似を用いて区間推定を行う。このとき,$\displaystyle\frac{\hat\beta-\beta}{se(\hat\beta)}$は標準正規分布に従う。統計ソフトウェアの結果から,回帰係数の推定値は$\hat\beta=-60.263$,標準誤差は$se(\hat\beta)=4.414$なので,$90\%$信頼区間の場合
$$\begin{align}&P\left(z_{-0.05}\le\frac{-60.263-\beta}{4.414}\le z_{0.05}\right)\ge0.90\\&\ \Rightarrow\ \ P\left(|-60.263-\beta|\le1.645\times4.414\right)\ge0.90\\
&\therefore\ \ \beta=-60.263\pm1.645\times4.414=[67.524, 53.002]\end{align}$$仮に$t$分布を用いた場合,$z_{0.05}$の代わりに自由度$197-2=195$の$t$分布の上側$5\%$値$t_{0.05}(195)$を使う。この値は$1.652$となり,$$\beta=-60.263\pm1.652\times4.414=[67.555, 52.971]$$となる。
