過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定2級(2019.06)【問題】(統計検定公式)<※期間限定>
- 統計検定2級(2019.06)【正解】(統計検定公式)
問10 解答
(幾何分布)
[1]
$\boxed{ \ \mathsf{18}\ }$ ①
不在→不在→在宅の確率を求める$$(1-0.2)\times(1-0.2)\times0.2=0.128$$
[2]
$\boxed{ \ \mathsf{19}\ }$ ②
在宅を成功,不在を失敗と考えると,在宅しているまでの訪問回数 $X$ は成功確率 $p=0.2$ の幾何分布に従う。期待値,分散は,$$E[X]=\frac1p=\frac1{0.2}=5,\ \ V[X]=\frac{1-p}{p^2}=\frac{1-0.2}{0.2^2}=20$$
※成功か失敗しかない試行をベルヌーイ試行という。成功確率は $p$。
このベルヌーイ試行を独立に何回も行うとき,初めて成功するまでに“試行”した回数を $X$ とすると,$X$ の確率関数は$$P(X=x)=p(1-p)^{x-1}$$となり,この確率分布をパラメータ $p$ の幾何分布という。(本によっては,初めて成功するまでに“失敗”した回数を $X$ とする定義の仕方もある。)
ここで,等比級数の和$$\displaystyle \sum_{x=0}^\infty a^x=\frac1{1-a}\ \ \ (|a|<1)$$の両辺を $a$ で微分すると$$\displaystyle \sum_{x=0}^\infty xa^{x-1}=\frac1{(1-a)^2}$$さらに,この式の両辺を $a$ で微分すると,$$\displaystyle \sum_{x=0}^\infty x(x-1)a^{x-2}=\frac2{(1-a)^3}$$となる。これを利用して,幾何分布の期待値と分散を求める。$$\begin{align}E[X]=&\sum_{x=0}^\infty xp(1-p)^{x-1}=p\sum_{x=0}^\infty x(1-p)^{x-1}\\=&\frac{p}{\{1-(1-p)\}^2}=\frac1p\\V[X]=&E[X(X-1)]+E[X]-E[X]^2\\=&\sum_{x=0}^\infty x(x-1)p(1-p)^{x-1}+\frac1p-\frac1{p^2}\\=&p(1-p)\sum_{x=0}^\infty x(x-1)(1-p)^{x-2}+\frac1p-\frac1{p^2}\\=&\frac{2p(1-p)}{\{1-(1-p)\}^3}+\frac1p-\frac1{p^2}\\=&\frac{2-2p}{p^2}+\frac{p}{p^2}-\frac1{p^2}=\frac{1-p}{p^2}\\\end{align}$$
問11 解答
(標準正規分布)
$\boxed{ \ \mathsf{20}\ }$ ⑤
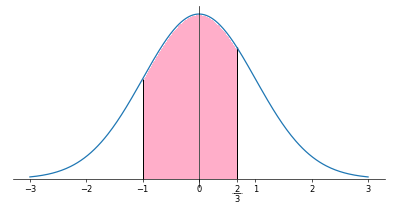
$\displaystyle Z=\frac{X-2}{\sqrt{9}}=\frac{X-2}{3}$ は標準正規分布 $N(0,1)$に従う。よって,$$\begin{align}P(-1<X\le4)=&P\left(\frac{-1-2}{3}<Z\le\frac{4-2}{3}\right)\\=&P\left(-1<Z\le\frac23\right)\\=&P\left(-1<Z\le0\right)+P\left(0<Z\le0.67\right)\\=&1-P(Z>1)-P(Z>0.67)\\=&1-0.1587-0.2514\\=&0.5899\\\end{align}$$確率関数の性質:$P(a<X<b)=P(X>a)-P(X>b)$,
正規分布は $x$ 軸に対称:$P(X<-a)=P(X>a)$
問12 解答
(不偏分散,$t$ 分布)
$\boxed{ \ \mathsf{21}\ }$ ④
標本平均の標準化 $\displaystyle\frac{\bar X-\mu}{\sqrt{\sigma^2/n}}$ は標準正規分布 $N(0,1)$ に従う。
標本平均の標準化の母平均 $\sigma^2$ を不偏分散 $S^2$ に置き換えた $\displaystyle\frac{\bar X-\mu}{\sqrt{S^2/n}}$ は自由度 $n-1$ の $t$ 分布 $t(n-1)$ に従う。$$P(\bar X\ge\mu+0.62S)=P\left(\frac{\bar X-\mu}{S}\ge0.62\right)=P\left(\frac{\bar X-\mu}{S/\sqrt{9}}\ge0.62\times\sqrt{9}=1.86\right)\\$$$\displaystyle\frac{\bar X-\mu}{S/\sqrt{9}}$ は自由度 $8$ の $t$ 分布に従うので,$$P\left(\frac{\bar X-\mu}{S/\sqrt{9}}\ge1.86\right)=0.05$$
問13 解答
(幾何分布)
[1]
$\boxed{ \ \mathsf{22}\ }$ ④
$\begin{align}p_3=P(\bar X=3)=&P(X_1=2,X_2=4)+P(X_1=4,X_2=2)\\=&\frac1{16}\times2=\frac18\\p_6=P(\bar X=6)=&P(X_1=4,X_2=8)+P(X_1=8,X_2=4)+P(X_1=6,X_2=6)\\=&\frac1{16}\times3=\frac3{16}\end{align}$$
[2]
$\boxed{ \ \mathsf{23}\ }$ ③
$\bar X$の分布は $\{2,3,3,4,4,4,5,5,5,5,6,6,6,7,7,8\}$
よって,中央値 $5$,最頻値 $5$
[3]
$\boxed{ \ \mathsf{24}\ }$ ⑤
$\bar X$ の期待値は$$E[\bar X]=E\left[\frac{X_1+X_2}{2}\right]=\frac{E[X_1]+E[X_2]}{2}=\frac{5+5}{2}=5$$により求められる。したがって,①,②,③,④は誤りで,⑤が正しい。
問14 解答
(母比率の区間推定)
$\boxed{ \ \mathsf{25}\ }$ ④
成功確率$p$の試行を$n$回行うときに成功する回数$X$は二項分布$B(n,p)$に従う。
$\therefore\ \ E(X)=np,\ V(X)=np(1-p)$
このとき,$n$がある程度大きいときは,中心極限定理によって,$B(n,p)$は正規分布$N(np,np(1-p))$に近似できる。よって,$X$を標準化すると標準正規分布$N(0,1)$に従う。$$Z=\frac{X-np}{\sqrt{np(1-p)}}=\frac{X/n-p}{\sqrt{\frac{p(1-p)}n}}\sim N(0,1)$$ここで,標本平均 $\hat p=x/n$は$p$の一致推定量なので,$n$が十分大きいとき$p$は$\hat p$に置き換えられる。
したがって,母比率の$100(1-\alpha)\%$信頼区間は,標準正規分布の上側 $100\alpha/2\%$ 点を $z_{\alpha/2}$とすると,$$P\left(\hat p-z_{\alpha/2}\sqrt{\frac{\hat p(1-\hat p)}n}\le p\le\hat p+z_{\alpha/2}\sqrt{\frac{\hat p(1-\hat p)}n}\right)=1-\alpha$$
$200$ 匹捕獲して $20$ 匹に印がついているので,比率の推定値は $\hat p=20/200=0.1$
これから,目印の付いている魚の母比率の$95\%$信頼区間は,$n=200$,$\hat p=0.1$,$\alpha=0.05$として$$\hat p\pm z_{\alpha/2}\sqrt{\frac{\hat p(1-\hat p)}n}=0.100\pm1.96\times\sqrt{\frac{0.100\times(1-0.100)}{200}}=0.100\pm0.042$$
問15 解答
(母平均の区間推定,母平均の検定(母分散の値が未知の場合))
[1]
$\boxed{ \ \mathsf{26}\ }$ ③
母分散の値が未知のとき,母分散 $\sigma^2$ の代わりに不偏分散 $s^2$ を用いた統計量$$t=\frac{\bar x-\mu}{\sqrt{s^2/n}}$$は自由度 $n-1$ の $t$ 分布 $t(n-1)$ に従う。区間推定のためには,上側確率が $\alpha/2$ となる値 $t_{\alpha/2}(n-1)$ を求めると,$$P(|t|\le t_{\alpha/2}(n-1))=1-\alpha$$となるので,母平均の $100(1-\alpha)\%$ 信頼区間は$$\left|\frac{\bar x-\mu}{\sqrt{s^2/n}}\right|\le t_{\alpha/2}(n-1)\\\therefore\ \bar x-t_{\alpha/2}(n-1)\sqrt{s^2/n}\le\mu\le\bar x+t_{\alpha/2}(n-1)\sqrt{s^2/n}$$
これから,母比率の$95\%$信頼区間は,$\bar x=3.23$,$n=24$,$s^2=8.72^2$,$\alpha=0.05$ として $t_{0.025}(23)=2.069$ なので,$$3.23-2.069\sqrt{8.72^2/24}\le\mu\le3.23+2.069\sqrt{8.72^2/24}\\3.23-3.682\le\mu\le3.23+3.682$$
[2]
$\boxed{ \ \mathsf{27}\ }$ ③
帰無仮説 $\mu=0$,対立仮説 $\mu>0$ の場合の棄却域は,有意水準 $100\alpha\%$ として,$$t=\frac{\bar x-0}{\sqrt{s^2/n}}>t_\alpha(n-1)$$
ここで,$\bar x=3.23$,$n=24$,$s^2=8.72^2$ とすると,$$t=\frac{3.23-0}{\sqrt{8.72^2/24}}=1.814$$$t_{0.05}(23)=1.714$,$t_{0.025}(23)=2.060$なので,有意水準 $5\%$ で棄却できるが,有意水準 $2.5\%$ では棄却できない。
問16 解答
(第一種の過誤,第二種の過誤,検出力)
| 真実 | |||
| 帰無仮説が正しい | 対立仮説が正しい | ||
| 検定の結果 | 帰無仮説を棄却しない (対立仮説が正しいとは言えない) | 正しい | 第二種の過誤(β) |
| 帰無仮説を棄却する (対立仮説が正しい) | 第一種の過誤(α) 有意水準 | 正しい 検出力(1-β) | |
[1]
$\boxed{ \ \mathsf{28}\ }$ ②
帰無仮説 $H_0:\theta=0$ のもとで,$X\sim N(0,1)$。よって,棄却域を $x\ge0.8$ と定めたときの第1種過誤の確率 $\alpha$ は$$\alpha=P(x\ge0.8|H_0)=0.2119$$ 対立仮説 $H_1:\theta=1$ のもとで,$X\sim N(1,1)\Rightarrow X-1\sim N(0,1)$。よって,棄却域を $x\ge0.8$ と定めたときの第2種過誤の確率 $\beta$ は$$\begin{align}\beta=&P(x<0.8|H_1)=P(x-1<0.8-1|H_1)\\=&P(x-1>0.2|H_1)=0.4207\end{align}$$
[2]
$\boxed{ \ \mathsf{29}\ }$ ①
棄却域を $x\ge x_0$ としたとき
第1種過誤の確率 $\alpha(x_0)=P(x\ge x_0)$
第2種過誤の確率 $\beta(x_0)=P(x/le x_0-1)=P(x\ge 1-x_0)$
$x_0=0.0, 0.5, 1.0$の時の$1-\alpha(x_0), \beta(x_0)$の値を標準正規分布表を使い求める。
$x_0=0.0$のとき、$1-\alpha(x_0)=1-P(x\ge 0.0)=1-0.5000=0.5000, \beta(x_0)=P(x\ge 1-0.0)=0.1587$
$x_0=0.5$のとき、$1-\alpha(x_0)=1-P(x\ge 0.5)=1-0.3085=0.6915, \beta(x_0)=P(x\ge 1-0.5)=0.3085$
$x_0=1.0$のとき、$1-\alpha(x_0)=1-P(x\ge 1.0)=1-0.1587=0.8413, \beta(x_0)=P(x\ge 1-1.0)=0.5000$
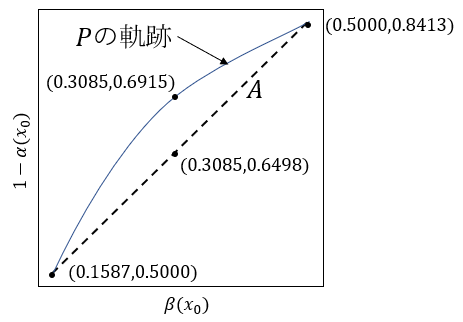
ここで、$x_0=0.0$のグラフ上の点の座標と$x_0=0.1$のグラフ上の点の座標とを結ぶ直線$A$の傾きを求めると、
$$a=\frac{0.8413-0.5000}{0.5000-0.1587}=1.000$$
この直線$A$上の$\beta(0.5)=0.3085$の時の点の$y$座標の値を求めると
$$a(0.3085-0.1587)-0.5000=0.6498$$
この値が$1-\alpha(0.5)=0.6915$より小さいということは、問題の点$P$の軌跡は直線$A$よりも上に凸の形になっているといえる。直線$A$の傾きが正なので、点$P$の軌跡は左下から右上に向かう上に凸の曲線となる。
[3]
$\boxed{ \ \mathsf{30}\ }$ ②
$\alpha(x_0)+\beta(x_0)$が最小になるということは、 $1-\alpha(x_0)-\beta(x_0)$が最大となることと等しい。
$x_0=0.0, 0.5, 1.0$の時の$1-\alpha(x_0)-\beta(x_0)$の値は
$x_0=0.0$のとき、$1-\alpha(x_0)=1-P(x\ge 0.0)-\beta(x_0)=0.5000-0.1587=0.3413$
$x_0=0.5$のとき、$1-\alpha(x_0)=1-P(x\ge 0.5)-\beta(x_0)=0.6915-0.3085=0.3830$
$x_0=1.0$のとき、$1-\alpha(x_0)=1-P(x\ge 1.0)-\beta(x_0)=0.8413-0.5000=0.3413$
となっており、グラフが上に凸となっていることから、$1-\alpha(x_0)-\beta(x_0)$が最大となるのは$0\lt x_0\lt 1$にあることがわかる。選択肢の中でこれを満たすのは②のみである。
問17 解答
(重回帰モデル,単回帰モデル,ダミー変数を用いた回帰)
[1]
$\boxed{ \ \mathsf{31}\ }$ ②
Ⅰ.問題のモデルの場合,高校卒は $C=U=G=0$ とした場合にあてはまるので,高校卒ダミー変数をモデルに組み込む必要がない。仮に組み込んだとすると,ダミー変数間に関係性ができるので,正しく推計を行うことができない。誤り。
Ⅱ.ダミー変数を使った回帰モデルの場合,回帰係数はダミー変数が $1$ の時の説明変数に与える増分になるので,回帰係数の差は説明変数に与える増分の差になる。正しい。
Ⅲ.データ数(観測数)を $n$,説明変数の数を $p$ とすると,回帰係数の $t_-$ 値は自由度 $n-p-1$ の $t$ 分布に従い,$P_-$ 値はこれにより計算される。問題のケースでは,自由度は $16-3-1=12$ となる。誤り。
[2]
$\boxed{ \ \mathsf{32}\ }$ ①
Ⅰ.教育年数の回帰係数の値は,教育年数が $1$ 増えるごとに初任給に対する増分である。正しい。
Ⅱ.被説明変数 $y$ の変動を示す総平方和 $S_y = \sum_i(y_i-\bar y)^2$ は,回帰平方和 $S_R = \sum_i(\hat y_i-\bar y)^2$ と残差平方和 $S_e = \sum_i(y_i-\hat y_i)^2$ の和に分解できる。この回帰平方和 $S_R$ が総平方和 $S_y$ に占める割合が決定係数 $R^2=S_R/S_y$である。
一方,説明変数が増えると残差平方和は小さくなる(証明略)ので,決定係数
$$R^2=\frac{S_R}{S_y}=\frac{S_y-S_e}{S_y}=1-\frac{S_e}{S_y}$$
は大きくなる性質がある。そこで,説明変数の数が異なるモデルの比較に利用される指標として,自由度調整済み決定係数 $R^{*2}$ が次式により定義される。
$$R^{*2}=1-\frac{S_e/(n-p-1)}{S_y/(n-1)}$$
この定義式から,単回帰モデルの決定係数と自由度調整済み決定係数は等しくないことがわかる。誤り。
Ⅲ.統計量 $t=\hat\alpha/se(\hat\alpha)$ としたとき,
両側検定 $H_0:\alpha=0,\ \ H_1:\alpha\ne0$ の棄却域は $|t|\ge t_{a/2}(n-p-1)$($a$は有意水準)
一方,片側検定 $H_0:\alpha=0,\ \ H_1:\alpha>0$ の棄却域は $t\ge t_a(n-p-1)$
よって,両側検定と片側検定では $P_-$ 値は異なる。誤り。
[3]
$\boxed{ \ \mathsf{33}\ }$ ⑤
Ⅰ.説明変数の数が異なるモデルの比較にあたっては,決定係数を用いず,自由度調整済み決定係数を用いる。誤り。
Ⅱ.学歴ダミー変数を用いた重回帰モデルでは,学歴間の初任給の変化は回帰係数の変化で表される。一方,教育年数を使った単回帰モデルでは,初任給は教育年数に比例して変化するので,学歴間の変化は同じである。正しい。
Ⅲ.学歴ダミー変数を使っているため,中学卒という新たな説明変数を投入して予測することは不可能である。教育年数を使った単回帰モデルにおいては中学卒に相当する教育年数 $x=9$ を設定することができるので形式的には予測は可能である。正しい。
問18 解答
(単回帰モデル,統計ソフトウェアの活用)
※重回帰モデルの統計ソフトウェアによる出力結果の主な項目
$\mathtt{Estimate}$:回帰係数($\alpha_0,\beta_1,\beta_2$)の推定値
$\mathtt{Std.Error}$:回帰係数の推定値の標準誤差
$\mathtt{t\ value}$:$t$値,$\mathtt{Pr(\gt|t|)}$:$P_-$値・・・回帰係数の検定で使う
$\mathtt{Rasidual\ standard\ error}$:誤差項の標準偏差の推定値
$\mathtt{degrees\ of\ freedom}$:自由度
$\mathtt{Multiple\ R-squared}$:決定係数($R^2$)
$\mathtt{Adjusted\ R-squared}$:自由度調整済み決定係数($R^{*2}$)
$\mathtt{F-statistic}$:$F$検定統計量,$\mathtt{p-value}$:$P_-$値・・・回帰の有意性の検定で使う
[1]
$\boxed{ \ \mathsf{34}\ }$ ⑤
$P_-$ 値が有意水準 $5\%$ を下回ると回帰係数は有意といえる。
[2]
$\boxed{ \ \mathsf{35}\ }$ ③
① $\mathtt{Multiple\ R-squared}$ は決定係数,$\mathtt{Adjusted\ R-squared}$ は自由度調整済み決定係数を表しているので,値の大小が正規性の仮定に関係がない。誤り。
② $\mathtt{t\ value}$ と検定統計量として $t$ 検定を行うことによって変数が有意であるか(確率的に$0$になりえないか)を判断する。$\mathtt{t\ value}$ の正負で変数の説明力を判断することはない。誤り。
③ 1人当たり乗用車数の回帰係数が負であることから,1人当たり乗用車数が多いほど1人当たり小売店舗事業所数は少なくなる。正しい。
④ $\mathtt{F-statistic}$ の値は回帰係数がすべて $0$ であるという帰無仮説の検定に用いられるが,その回帰係数には定数項は含まれない。誤り。
⑤ 重回帰分析で変数の数を増減させてモデルを比較する際は。決定係数$(\mathtt{Multiple\ R-squared})$ではなく,自由度調整済み決定係数$(\mathtt{Adjusted\ R-squared})$が大きいモデルを選択する。誤り。
![日本統計学会公式認定 統計検定 2級 公式問題集[2018〜2021年]](https://m.media-amazon.com/images/I/51PRkPbugTL._SL500_.jpg)