過去問題
過去問題は統計検定公式問題集が問題と解答例を公開しています。こちらを参照してください。
- 統計検定2級（2019.06）【問題】（統計検定公式）＜※期間限定＞
- 統計検定2級（2019.06）【正解】（統計検定公式）
問1 解答
（相対度数，度数分布）
[1]
$\boxed{ \ \mathsf{1}\ }$ ③
2008年における貯蓄額が $2000$ 万円以上世帯の相対度数が $19.6\%$ なので
$5.3+3.8+4.7+$ (イ) $=19.6\ \Rightarrow\ $ (イ) $=19.6-5.3-3.8-4.7=5.8$
[2]
$\boxed{ \ \mathsf{2}\ }$ ①
Ⅰ．歪度は，右に裾が長い分布では正の値になり，左に裾が長い分布では負の値になる。誤り。
2015年の各階級における累積相対度数を求めると，
(Ｇ)の累積度数 $13.2+7.2+7.0+6.1+5.6+5.5+4.5=49.1$
(Ｈ)の累積度数 $49.1+4.2=53.3$
よって，中央値が含まれる階級は(Ｈ)。
[3]
$\boxed{ \ \mathsf{3}\ }$ ⑤
2015年の平均値のある階級とその一つ下の階級における累積相対度数を求めると，
(Ｋ)の累積度数 $53.3+3.3+3.2+6.0=65.8\ $（[2]の結果を利用）
(Ｌ)の累積度数 $65.8+4.6=70.2$
よって，貯蓄額が平均未満の世帯の割合は $65.8\%\sim70.2\%$。１の位で四捨五入すると $70\%$。
問2 解答
（散布図，相関係数，共分散，変動係数）
[1]
$\boxed{ \ \mathsf{4}\ }$ ④
国語と数学の相関係数は $0.72$ で，正の相関がやや強い関係である。散布図で点の分布が左下から右上に分布している④と⑤のグラフのうち，⑤はかなり強い相関である。
[2]
$\boxed{ \ \mathsf{5}\ }$ ②
標準偏差 $s_x,s_y$ 共分散 $s_{xy}$ のとき，相関係数は $\displaystyle\frac{s_{xy}}{s_xs_y}$ となるので，$$\frac{s_{xy}}{12.5\times16.4}=0.72\ \Rightarrow\ s_{xy}=0.72\times12.5\times16.4=147.6$$
[3]
$\boxed{ \ \mathsf{6}\ }$ ②
値を２倍にすると，平均は２倍，分散は４倍，標準偏差は２倍。
したがって，変動係数は標準偏差／平均なので，変わらない。
共分散は，２つのデータの平均からの偏差の積の和なので，片方のデータの平均からの偏差が２倍となれば，２倍となる。
※上記のことを式で書くと，
数学の得点を $x_i$，国語の得点を $y_i$ とする。数学の得点を２倍 $x’_i=2x_i$ としたとき，
平均 $\displaystyle\bar x’=\frac1n\sum{2x_i}=2\times\frac1n\sum{x_i}=2\bar x$
分散 $\displaystyle s^2_{x’}=\frac1n\sum(2x_i-\bar x’)^2=\frac1n\sum(2x_i-2\bar x)^2=4\times\frac1n\sum(x_i-\bar x)^2=4s^2_x$
標準偏差 $s_{x’}=2s_x$
変動係数 $\displaystyle\frac{s_{x’}}{\bar x’}=\frac{2s_x}{2\bar x}=\frac{s_x}{\bar x}$
共分散 $\displaystyle s_{x’y}=\frac1n\sum(2x_i-\bar x’)(y_i-\bar y’)=\frac1n\sum(2x_i-2\bar x)(y_i-\bar y’)=2\times\frac1n\sum(x_i-\bar x)(y_i-\bar y’)=2s_{xy}$
問3 解答
（標準化得点）
[1]
$\boxed{ \ \mathsf{7}\ }$ ④
Ⅰ．標準化得点の平均は $0$，標準偏差は $1$。正しい。
Ⅱ．データの最大値となるマイアミの標準化得点は $\displaystyle z_{14}=\frac{22-2.4}{7.0}=2.8$ となり，これが標準化得点の最大値である。誤り。
Ⅲ．摂氏の平均，標準偏差を $\bar C$，$s_C$，華氏の平均，標準偏差を $\bar F$，$s_F$とすると，$\displaystyle\bar F=1.8\bar C+32,\ \ s_F=1.8s_C$ となるので，$\displaystyle w_i=\frac{F_i-\bar F}{s_F}=\frac{1.8C_i+32-(1.8\bar C+32)}{1.8s_C}=\frac{C_i-\bar C}{s_C}=z_i$。正しい。
[2]
$\boxed{ \ \mathsf{8}\ }$ ④
$\displaystyle\bar F=1.8\bar C+32=1.8\times2.4+32=36.32,\ \ s_F=1.8s_C=1.8\times7.0=12.6$
問4 解答
（相関係数，偏相関係数）
[1]
$\boxed{ \ \mathsf{9}\ }$ ①
Ⅰ．相関係数が $+1.0$ に近い値になると，散布図上でデータをプロットすると，傾きが正の直線付近にプロットされるようになる。正しい。
Ⅱ．偏相関係数は２つの変数間の相関関係に，別の第３の変数による影響があると思われるときに，その変数の影響を除いた相関関係を見るための係数である。その関係は必ずしも非線形関係であるとは限らない。誤り。
Ⅲ．偏相関係数の符号は，２変数の相関係数と第３の変数と各変数の相関係数の大小関係で決まる。相関係数や偏相関係数の符号から，相関関係の有無を論ずることはない。誤り。
[2]
$\boxed{ \ \mathsf{10}\ }$ ③
Ⅰ～Ⅲは，同じ相関係数と偏相関係数の結果に対して，異なる結論を導き出している文章であるので，どれか１つが正解である。
相関係数が高い２つの変数間に対して，別の第３の変数の影響を除去した偏相関係数が，元の相関係数より相関関係が悪くなった場合，２つの変数は第３の変数を介して，見かけ上高い相関が得られたといえる（元のそれぞれの変数は第３の変数との相関が良いからである）。この見かけ上の相関関係を擬相関という。
問5 解答
（フィッシャーの三原則）
$\boxed{ \ \mathsf{11}\ }$ ①
フィッシャーの３原則：無作為化，繰り返し，局所管理
Ⅰ．無作為化：対象の抽出，処理の順番など，均一にできない条件については無作為に割り付ける。これにより，制御できない条件は偶然による誤差に置き換えることができる。正しい。
Ⅱ．繰り返し：ばらつきや個体差の影響を見積もるために実験を繰り返しを行う。同じ被験者で繰り返しても，その被験者についての結果しか得られないので，繰り返しにはならない。誤り。
Ⅲ．局所管理：処理効果以外のばらつきを小さくするため，条件が均一になるようブロック化する。条件設定の管理を行えばよく，管理といっても実際に監督・監視する必要はない。誤り。
問6 解答
（標本抽出法）
$\boxed{ \ \mathsf{12}\ }$ ⑤
① 多段抽出法は，母集団をいくつかのグループ(第1段抽出単位)に分け，そこから無作為抽出でいくつかグループを選び，さらにその中から無作為抽出でいくつかのグループ(第2段抽出単位)を選び・・を何段か繰り返してそこから標本を<u>無作為に</u>抽出する。段数が多くなるほど推定精度は悪くなる。誤り。
② 系統抽出法は，通し番号をつけた名簿を作成し，1番目の調査対象を無作為に選び、2番目以降の調査対象を一定の間隔で抽出する方法（問題文の抽出方法は層化抽出法）。誤り。
③ 無作為抽出法では，回答率が低いと母集団からまんべんなく抽出できず，偏った標本を得ることになる可能性があるため，精度は高くないことが考えられる。誤り。
④ 系統抽出は，単純無作為抽出法に類似した簡便な抽出法であって，精度が高くなるわけではない。誤り。
⑤ 集落(クラスター)抽出法は，母集団を小集団であるクラスター（集落）に分け，その中からいくつかのクラスターを無作為に抽出し，それぞれのクラスターにおいて<u>全数調査</u>を行う。正しい。
問7 解答
（事象と確率，排反，独立）
$\boxed{ \ \mathsf{13}\ }$ ②
事象 $A$ と $B$ は独立 $\Leftrightarrow\ P(A\cap B)=P(A)P(B)$
事象 $A$ と $B$ は排反 $\Leftrightarrow\ P(A\cap B)=0$
そこで，$P(A\cap B)$ を求める。
$P(A\cap B)=P(A)+P(B)-P(A\cup B)=0.4+0.35-0.61=0.14\ \Rightarrow\ $排反でない。
$P(A)P(B)=0.4\times0.35=0.14=P(A\cap B)\ \Rightarrow\ $独立である。
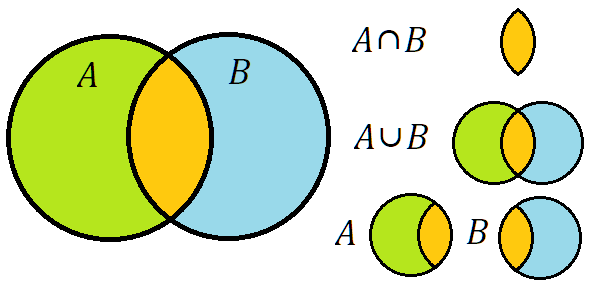
問8 解答
（条件付き確率，確率変数の期待値）
[1]
$\boxed{ \ \mathsf{14}\ }$ ⑤
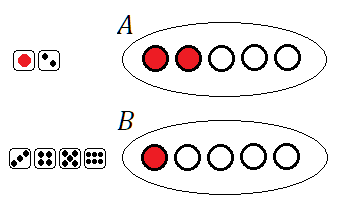
サイコロを $1$ 回投げて $3$以上の目が出る確率＝袋 $B$ を選ぶ確率$$p_1=\frac46=\frac23$$
袋 $B$ から $2$回玉を取り出して赤玉を $1$ 回だけ引く確率＝赤→白または白→赤と取り出す確率$$p_2=\frac15\times\frac45+\frac45\times\frac15=\frac{8}{25}$$
よって求める確率は$$p_1\times p_2=\frac23\times\frac{8}{25}=\frac{16}{75}$$
[2]
$\boxed{ \ \mathsf{15}\ }$ ⑤
確率変数 $X$ の取りうる値は $\{0,1,2\}$
$$\begin{align}P(X=0)=&\frac13\times\frac35\times\frac35+\frac23\times\frac45\times\frac45=\frac{41}{75}\\P(X=1)=&\frac13\times\left(\frac25\times\frac35+\frac35\times\frac25\right)+\frac23\times\left(\frac15\times\frac45+\frac45\times\frac15\right)=\frac{28}{75}\\P(X=2)=&\frac13\times\frac25\times\frac25+\frac23\times\frac15\times\frac15=\frac{6}{75}\\\therefore\ E(X)=&\sum_{x=0}^2xP(X=x)=0\times\frac{41}{75}+1\times\frac{28}{75}+2\times\frac{6}{75}=\frac{40}{75}=\frac{8}{15}\end{align}$$
問9 解答
（確率変数の共分散，相関係数）
[1]
$\boxed{ \ \mathsf{16}\ }$ ③
$$\begin{align}\mathrm{Cov}[X,Y]=&E[XY]-E[X]E[Y]=4-1\times2=2\\V[Z]=&V[X+Y]=V[X]+V[Y]+2\mathrm{Cov}[X,Y]=24\\&\Rightarrow\ V[X]+V[Y]=24-2\times2=20&\cdots(a)\\V[W]=&V[2X-Y]=4V[X]+V[Y]-2\times2\mathrm{Cov}[X,Y]=24\\&\Rightarrow\ 4V[X]+V[Y]=24+2\times2\times2=32&\cdots(b)\\(b)-(a)\ \ 3V[X]=&12\Rightarrow V[X]=4\\E[X^2]=&V[X]+E[X]^2=4+1^2=5\\(a)\ \ V[X]+V[Y]=&20\ \Rightarrow\ V[Y]=20-V[X]=20-4=16\\E[Y^2]=&V[Y]+E[Y]^2=16+2^2=20\end{align}$$
[2]
$\boxed{ \ \mathsf{17}\ }$ ④
$$\rho=\frac{\mathrm{Cov}[X,Y]}{\sqrt{V[X]}\sqrt{V[Y]}}=\frac{2}{\sqrt{4}\sqrt{16}}=\frac{2}{2\times4}=0.25$$